机器学习基础-day07-项目案例

1 房价预测

线性回归是一种用于建模和分析关系的线性方法。在简单线性回归中，我们考虑一个自变量和一个因变量之间的关系，用一条直线进行建模。

而在多元线性回归中，我们可以使用多个自变量来建模，因此我们需要拟合的不再是一个简单的直线，而是在高维空间上的一个超平面。每个样本的因变量（y）在多元线性回归中依赖于多个自变量（x），这样的关系可以用一个超平面来表示，这个超平面被称为回归平面。

因此，在多元线性回归中，我们试图找到一个最适合数据的超平面，以最小化实际观测值与模型预测值之间的差异。

2 数据集

本例使用了一个房地产估价（Datasets - UCI Machine Learning Repository）数据集，其中包含关于房地产估价的市场历史数据集收集自台湾新北市新店区。数据以xlsx形式保存在dataset文件夹中，其中Real estate valuation data set.xlsx是数据，以下是数据集的中文解释：

表中一共有8列

列名	角色	类型	描述	单位	缺失值
No	无	整型	第几个样本	无	无
X1 transaction date	输入特征1	浮点型	交易日期，按照一年的365所占比例计算	年	无
X2 house age	输入特征2	浮点型	房龄	年	无
X3 distance to the nearest MRT station	输入特征3	浮点型	距离最近的地铁站的距离	米	无
X4 number of convenience stores	输入特征4	整型	步行生活圈内便利店数量	个	无
X5 latitude	输入特征5	浮点型	纬度	度	无
X6 longitude	输入特征6	浮点型	经度	度	无
Y house price of unit area	目标	浮点型	一平方米的单位房价	万新台币/平方米	无

上面的X和Y数据中，X4是整型，不符合数据的连续特征，后期在训练前需要单独处理。

通过数据集字段的介绍我们可以明确我们的任务是通过不同的特征对房地产估价进行线性回归预测。

代码运行，使用JupyterLab写代码

2 预测红酒的品质

2.1 数据集

本例使用了一个葡萄酒（UCI Machine Learning Repository）数据集，其中包含红酒的各种含量数值。数据以csv形式保存，其中winequality-red.csv是数据，以下是数据集的中文解释：

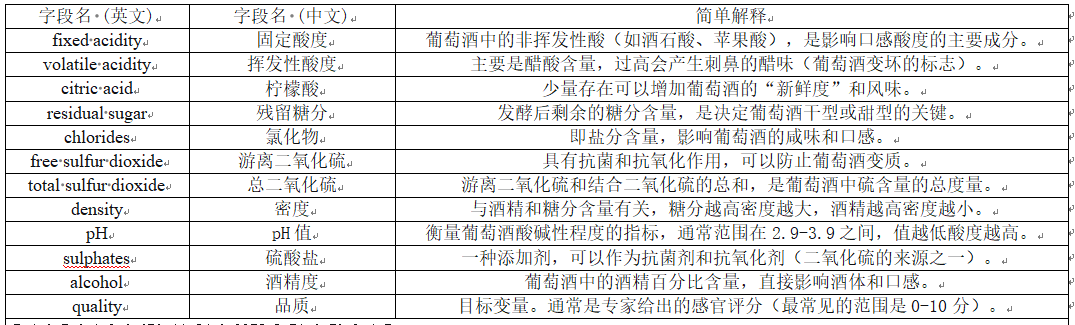
上面的X和Y数据中，free sulfur dioxide、total sulfur dioxide、quality是整型，不符合数据的连续特征，后期在训练前需要单独处理。

通过数据集字段的介绍我们可以明确我们的任务是通过不同的特征对红酒的品质进行线性回归预测。

代码运行，使用JupyterLab写代码