当前位置：首页 > news >正文

决策树算法详解：从原理到实战

news 2025/9/5 16:06:26

决策树算法详解：从原理到实战

本文带你深入理解决策树算法的核心思想、主流模型（ID3、C4.5、CART）、构建流程、剪枝策略，并结合真实案例进行解析。

引言：我们每个人都是“决策树”

想象一下，你准备去水果摊买一个西瓜，你是这样挑选的：

你：老板，这瓜保熟吗？
老板：瓜蒂是弯曲的，说明熟了。
你：那敲起来声音怎么样？
老板：声音清脆，是好瓜。
你：纹路清晰吗？
老板：特别清晰，沙瓤瓜！
你：那好，来一个！

这个挑选过程，本质上就是一个决策树——通过一系列“if-else”判断（瓜蒂形状、敲击声音、表面纹路），最终做出“买”或“不买”的分类决策。

在机器学习中，决策树（Decision Tree） 正是模拟人类这种直观的逻辑判断过程，是一种强大的监督学习算法，广泛应用于分类与回归任务。

一、什么是决策树？

决策树是一种树形结构，其中：

根节点（Root Node）：代表整个数据集，是决策的起点。
内部节点（Internal Node）：表示一个特征上的判断条件（如“年龄 > 30”）。
分支（Branch）：表示某个判断条件的结果（如“是”或“否”）。
叶子节点（Leaf Node）：代表最终的分类结果或预测值（如“同意贷款”）。

决策树的构建三步走：

特征选择：挑选最具区分能力的特征作为分裂依据。
树的生成：递归地根据特征划分数据，生成子树。
剪枝（Pruning）：防止过拟合，提升模型泛化能力。

二、经典决策树算法详解

1. ID3：基于信息增益的分类树

提出时间：1975年
核心思想：选择信息增益最大的特征进行分裂。

（1）信息熵（Entropy）

熵是信息论中衡量不确定性的指标。熵越大，数据越混乱；熵越小，数据越纯净。

公式：
$-\sum_{k=1}^{K} p_k \log_2 p_k$
其中 $p_k$ 是第 $k$ 类样本在数据集 $D$ 中的比例。

举例：

若数据集完全纯净（如全是“同意”），则 $H (D) = 0$ 。
若数据集类别均匀分布（如“同意”和“拒绝”各占50%），则 $H (D) = 1$ 。

（2）信息增益（Information Gain）

信息增益衡量的是：使用某个特征划分数据后，系统不确定性减少了多少。

公式：
$g (D, A) = H (D) - H (D ∣ A)$
其中 $H (D ∣ A)$ 是在特征 $A$ 条件下的条件熵。

选择策略：计算所有特征的信息增益，选择增益最大的特征进行分裂。

（3）ID3 决策树构建流程

计算每个特征的信息增益。
使用信息增益最大的特征将数据集拆分为子集。
将该特征作为当前节点。
对每个子集递归执行上述步骤，直到满足停止条件。

（4）ID3 的局限

只能处理离散型特征。
倾向于选择取值较多的特征（如“用户ID”），容易过拟合。

2. C4.5：基于信息增益率的改进

提出时间：1993年
核心思想：使用信息增益率（Gain Ratio） 替代信息增益，缓解对多值特征的偏好。

公式：
$\text{Gain Ratio}(D, A) = \frac{g(D, A)}{IV(A)}$
其中分裂信息（Intrinsic Value）为：
$-\sum_{v=1}^{n} \frac{|D^v|}{|D|} \log_2\left(\frac{|D^v|}{|D|}\right)$

注： $D^v$ 表示特征 $A$ 取第 $v$ 个值时对应的样本子集。

本质：

对信息增益进行归一化，避免偏向取值多的特征。
特征取值越多， $I V (A)$ 越大，增益率越小，起到惩罚作用。

示例计算

编号	特征a	目标值
1	α	A
2	α	A
3	β	B
4	α	A
5	β	B
6	α	B

总熵：
$-\frac{3}{6}\log_2\left(\frac{3}{6}\right) - \frac{3}{6}\log_2\left(\frac{3}{6}\right) = 1$
条件熵（按特征a）：
- α 分支：4个样本（3A, 1B）
  $H_\alpha = -\frac{3}{4}\log_2\left(\frac{3}{4}\right) - \frac{1}{4}\log_2\left(\frac{1}{4}\right) \approx 0.811$
- β 分支：2个样本（2B）
  $H_\beta = 0$
- 条件熵：
  $\frac{4}{6} \times 0.811 + \frac{2}{6} \times 0 \approx 0.541$
信息增益：
$g (D, A) = 1 - 0.541 = 0.459$
分裂信息 $I V (A)$ ：
$-\frac{4}{6}\log_2\left(\frac{4}{6}\right) - \frac{2}{6}\log_2\left(\frac{2}{6}\right) \approx 0.918$
信息增益率：
$\text{Gain Ratio} = \frac{0.459}{0.918} \approx 0.5$

结论：C4.5 更倾向于选择增益率高的特征，避免 ID3 的偏差。

优点

可处理连续型特征（通过二分法）。
支持缺失值处理。
缓解了 ID3 对多值特征的偏好。

缺点

计算复杂度较高。
不适合超大规模数据集。

3. CART：分类与回归树

提出时间：1984年
核心思想：使用基尼指数（Gini Index） 作为分类标准，适用于分类和回归任务。

（1）基尼指数（Gini Index）

基尼值 Gini(D)：从数据集中随机抽取两个样本，其类别不同的概率。
$\text{Gini}(D) = 1 - \sum_{k=1}^{K} p_k^2$
基尼指数 Gini_index(D, A)：加权平均后的基尼值。
$Gini_index(D,A)=∑v=1V∣Dv∣∣D∣Gini(Dv) \text{Gini\_index}(D, A) = \sum_{v=1}^{V} \frac{|D^v|}{|D|} \text{Gini}(D^v)$

选择策略：选择使 基尼指数最小 的特征和分裂点。

（2）CART 的特点

支持分类与回归任务。
使用二叉树结构（每次分裂为两个子集）。
连续特征采用二分法寻找最优切分点。
回归树使用平方误差最小化作为分裂标准。

三者对比总结

名称	提出时间	分裂标准	特点
ID3	1975	信息增益	仅支持离散特征；偏好取值多的特征
C4.5	1993	信息增益率	支持连续特征与缺失值；计算较复杂
CART	1984	基尼指数 / 平方误差	支持分类与回归；二叉树结构；计算高效

三、实战案例：构建 CART 决策树（贷款拖欠预测）

数据集

序号	是否有房	婚姻状况	年收入(K)	是否拖欠贷款
1	yes	single	125	no
2	no	married	100	no
3	no	single	70	no
4	yes	married	120	no
5	no	divorced	95	yes
6	no	married	60	no
7	yes	divorced	220	no
8	no	single	85	yes
9	no	married	75	no
10	no	Single	90	Yes

注：目标变量共 4 个 “yes”，6 个 “no”。

1. 计算各特征的基尼指数

（1）是否有房

有房（yes）：3 个样本，均为 no
$\text{Gini}(\text{yes}) = 1 - (0)^2 - (1)^2 = 0$
无房（no）：7 个样本，4 个 no，3 个 yes
$\text{Gini}(\text{no}) = 1 - \left(\frac{3}{7}\right)^2 - \left(\frac{4}{7}\right)^2 \approx 0.4898$
加权基尼指数：
$Gini_index=310×0+710×0.4898≈0.343 \text{Gini\_index} = \frac{3}{10} \times 0 + \frac{7}{10} \times 0.4898 \approx 0.343$

（2）婚姻状况（以 “married” 为划分）

married：4 个样本，均为 no → Gini = 0
非 married（single, divorced）：6 个样本（3 no, 3 yes）
$\text{Gini} = 1 - \left(\frac{3}{6}\right)^2 - \left(\frac{3}{6}\right)^2 = 0.5$
加权基尼指数：
$\frac{4}{10} \times 0 + \frac{6}{10} \times 0.5 = 0.3$

（3）年收入（连续特征）

排序后取相邻均值作为候选切分点（如 87.5, 92.5, 97.5 等）。
经计算，最优切分点为 97.5，对应基尼指数为 0.3。

2. 第一轮分裂结果

特征	基尼指数
是否有房	0.343
婚姻状况	0.3
年收入（97.5）	0.3

选择 婚姻状况 或 年收入 均可（基尼指数最小）。通常优先选择离散特征或计算更稳定的特征。

假设选择 婚姻状况 作为根节点。

3. 第二轮分裂（右子树：非 married）

非 married 样本：序号 1, 3, 5, 8, 10（共 5 个？实际应为 6 个 → 1,3,5,8,10 → 修正：序号 1,3,5,8,10）

实际非 married：序号 1(single), 3(single), 5(divorced), 8(single), 10(single) → 共 5 个？
原始数据中 married 有 4 个（2,4,6,9），其余 6 个为非 married。

正确子集：1,3,5,7,8,10 → 6 个样本（3 no, 3 yes）

在该子集中继续计算“是否有房”和“年收入”的基尼指数，选择最优分裂。

（过程略，按相同方法递归）

四、回归决策树：预测连续值

与分类树不同，回归树预测的是连续值（如房价、销量）。

构建原理（CART 回归树）

项目	分类树	回归树
输出	离散类别	连续值
分裂标准	基尼指数	平方误差
预测值	多数类	叶子节点均值

回归树构建步骤

数据集

序号	$x$	$y$
1	1	5.56
2	2	5.70
3	3	5.91
4	4	6.40
5	5	6.80
6	6	7.05
7	7	8.90
8	8	8.70
9	9	9.00
10	10	9.05

第一轮：寻找最优切分点

对每个可能的切分点 $s$ （如 1.5, 2.5, …, 9.5），计算：

$\text{Loss}(s) = \sum_{x_i \leq s} (y_i - \bar{y}_L)^2 + \sum_{x_i > s} (y_i - \bar{y}_R)^2$

切分点 $s$	平方损失
1.5	15.72
2.5	12.07
3.5	8.36
4.5	5.78
5.5	3.91
6.5	1.93
7.5	8.01
8.5	11.73
9.5	15.74

选择 $x = 6.5$ 为第一分裂点。

左子树（ $x < 6.5$ ）：样本 1–6

继续寻找最优切分点：

切分点 $s$	损失
1.5	1.3087
2.5	0.7540
3.5	0.2771
4.5	0.4368
5.5	1.0644

选择 $x = 3.5$ 为分裂点。

右子树（ $x > 6.5$ ）：样本 7–10

切分点 $s$	损失
7.5	0.025
8.5	0.005
9.5	0.025

选择 $x = 8.5$ 为分裂点。

最终回归树结构

根节点 (x ≤ 6.5)
├── 左子树 (x ≤ 3.5) → 预测值：(5.56+5.7+5.91)/3 ≈ 5.72
└── 右子树 (x > 3.5) → 预测值：(6.4+6.8+7.05)/3 ≈ 6.75根节点 (x > 6.5)
├── 左子树 (x ≤ 8.5) → 预测值：(8.9+8.7)/2 = 8.8
└── 右子树 (x > 8.5) → 预测值：(9.0+9.05)/2 = 9.025

预测示例：若 $x = 8$ ，路径为： $x > 6.5$ → $x \leq 8.5$ → 输出 8.8。

五、演示线性回归和决策树回归对比

"""
结论：回归类的问题。即能使用线性回归，也能使用决策树回归优先使用线性回归，因为决策树回归可能比较容易导致过拟合
"""import  numpy as np
import  pandas as pd
from sklearn.tree import  DecisionTreeRegressor  #回归决策树
from sklearn.linear_model import  LinearRegression #线性回归
import matplotlib.pyplot as plt#1、获取数据
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])#2、创建线性回归 和 决策树回归
es1=LinearRegression()
es2=DecisionTreeRegressor(max_depth=1)
es3=DecisionTreeRegressor(max_depth=10)#3、模型训练
es1.fit(x,y)
es2.fit(x,y)
es3.fit(x,y)#4、准备测试数据 ，用于测试
# 起始, 结束, 步长.
x_test = np.arange(0.0, 10.0, 0.1).reshape(-1, 1)
print(x_test)#5、模型预测
y_predict1=es1.predict(x_test)
y_predict2=es2.predict(x_test)
y_predict3=es3.predict(x_test)#6、绘图
plt.figure(figsize=(10,5))#散点图
plt.scatter(x,y,color='gray',label='data')plt.plot(x_test,y_predict1,color='g',label='liner regression')
plt.plot(x_test,y_predict2,color='b',label='max_depth=1')
plt.plot(x_test,y_predict3,color='r',label='max_depth=10')plt.legend()
plt.xlabel("data")
plt.ylabel("target")plt.show()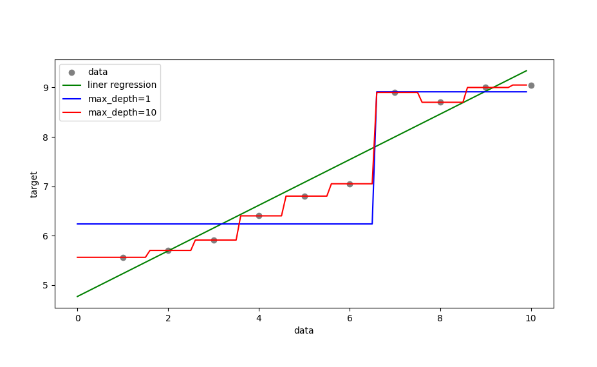

六、防止过拟合：决策树剪枝

目的：决策树剪枝是一种防止决策树过拟合的一种正则化方法；提高其泛化能力。
剪枝：把子树的节点全部删掉，使用用叶子节点来替换
预剪枝：指在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化性能提升，则停止划分并将当前节点标记为叶节点;
后剪枝：是先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化性能提升，则将该子树替换为叶节点。

1. 预剪枝（Pre-pruning）

思想：提前停止树的生长。
方法：
- 设置最大深度（max_depth）
- 设置内部节点最小样本数（min_samples_split）
- 设置叶子节点最小样本数（min_samples_leaf）
优点：训练快，防过拟合。
缺点：可能欠拟合，错过潜在模式。

2. 后剪枝（Post-pruning）

思想：先生成完整树，再自底向上剪枝。
方法：若将某子树替换为叶节点能提升验证集性能，则剪枝。
优点：泛化性能通常优于预剪枝。
缺点：训练时间长。

Scikit-learn 目前主要支持预剪枝，后剪枝需手动实现或使用 cost_complexity_pruning_path。

特性	预剪枝	后剪枝
优点	- 使决策树的很多分支没有展开，降低了过拟合风险 - 减少了决策树的训练、测试时间开销	- 比预剪枝保留了更多的分支 - 欠拟合风险很小，泛化性能往往优于预剪枝
缺点	- 有些分支的当前划分虽不能提升泛化性能，但后续划分却有可能导致性能的显著提高；带来了欠拟合的风险	- 训练时间开销比未剪枝的决策树和预剪枝的决策树都要大得多

七、Python 实战：泰坦尼克号生存预测

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score,classification_report
from sklearn.tree import plot_tree# 读取数据
data_df=pd.read_csv("../../data/train.csv")
data_df.info()# 数据预处理
data_df.fillna({'Age': data_df['Age'].mean()}, inplace=True)   # 用age列的平均值 来填充空值
# 获取特征和标签
x=data_df[['Pclass','Age','Sex']]   #船舱等级 、性别 、年龄
y=data_df['Survived']            #是否存活
x=pd.get_dummies(x)X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)# 构建决策树
clf = DecisionTreeClassifier(criterion='gini',              # 使用基尼指数（CART）max_depth=5,                   # 限制深度防止过拟合min_samples_split=10,          # 内部节点最小样本数min_samples_leaf=5,            # 叶子节点最小样本数random_state=42
)# 训练模型
clf.fit(X_train, y_train)# 预测与评估
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"准确率: {accuracy:.2f}")
print(f"分类评估报告:{classification_report(y_test,y_pred,target_names=['Died','Survivor'])}")# 绘图
# 设置画布大小
plt.figure(figsize=(50,30))
# 绘制决策树
#参1： 决策树分类器  参2：填充颜色   参3：层数
plot_tree(clf,filled=True,max_depth=30)# 具体绘制
plt.show()