当前位置：首页 > news >正文

（D题｜矿井突水水流漫延模型与逃生方案）2025年高教杯全国大学生数学建模国赛解题思路|完整代码论文集合

news 2025/9/5 13:16:39

我是Tina表姐，毕业于中国人民大学，对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在，我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合，专为本次赛题设计，旨在帮助您深入理解数学建模的每一个环节。
本次2025年高教杯全国大学生数学建模国赛C题可以做如下考虑 (部分公式和代码因为知乎排版问题显示不完整，文中代码仅有部分，完整论文格式标准，包含全部代码)

在这里插入图片描述

可视化

在这里插入图片描述

问题 1

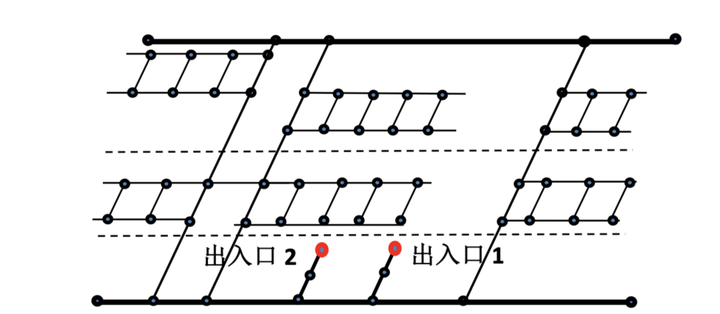
若巷道的某一点发生突水，试分析水流过程，建立突水水流在巷道的流动漫延模型。

对附件 1 和附件 2 给出的两个矿井巷道网络，分别给出网络中各巷道水流的变化情况，其中：

附件 1 中的突水点位置为 A1 (5349.03,4931.90,10.00)
附件 2 中的突水点位置为 A2 (4143.12,4376.28,6.33)

要求将结果分别保存到文件 result1-1.xlsx 和 result1-2.xlsx 中，其中需要计算：

端点水流到达时刻：突水水流首次流经该点的时刻
巷道充满水时刻：巷道中水流的水平面达到巷道最高点的时刻

这个问题的核心是建立水流在矿井巷道网络中的漫延传播模型，分析水流如何从突水点开始，沿着巷道网络向各个方向扩散的过程。
来为矿井突水水流漫延问题建立数学模型。

问题1：突水水流漫延数学模型

1. 问题分析

这是一个在三维巷道网络中的水流传播问题。需要考虑：

水流在重力作用下的流动
巷道网络的拓扑结构
水流在分叉点的分流规律
水流到达时间和充满时间的计算

2. 模型假设

巷道断面为矩形（宽4m，高3m）
水流初始水位为0.1m
突水量恒定为30 m³/min
水流在分叉点平均分流
水流优先向下流动（重力作用）

3. 数学模型建立

3.1 巷道网络表示

设巷道网络为有向图 G = (V, E)，其中：

V = {v₁, v₂, …, vₙ} 为端点集合
E = {e₁, e₂, …, eₘ} 为巷道集合

每个端点 vᵢ 有坐标 (xᵢ, yᵢ, zᵢ)

3.2 巷道参数计算

对于巷道 eᵢⱼ（连接端点 vᵢ 和 vⱼ）：

长度：

Lᵢⱼ = √[(xⱼ-xᵢ)² + (yⱼ-yᵢ)² + (zⱼ-zᵢ)²]

坡度：

sᵢⱼ = (zⱼ - zᵢ) / Lᵢⱼ

体积：

Vᵢⱼ = Lᵢⱼ × 4 × 3 = 12Lᵢⱼ (m³)

3.3 水流速度模型

考虑重力和坡度影响，水流速度为：

vᵢⱼ(t) = v₀ × (1 + α × sᵢⱼ)

其中：

v₀ = 2 m/s（基准流速）
α = 0.5（坡度影响系数）
sᵢⱼ > 0 表示下坡，sᵢⱼ < 0 表示上坡

3.4 水流传播时间

巷道传播时间：

Tᵢⱼ = Lᵢⱼ / vᵢⱼ

端点到达时间：
从突水点开始，使用Dijkstra算法计算最短时间路径：

T(vᵢ) = min{T(path) | path from source to vᵢ}

3.5 水位变化模型

对于任意时刻 t，巷道 eᵢⱼ 中的水量：

W(eᵢⱼ, t) = ∫[T(vᵢ)]^t Q(τ) × f(eᵢⱼ, τ) dτ

其中：

Q(t) = 30 m³/min（突水流量）
f(eᵢⱼ, t) 为该巷道在时刻t的分流系数

水位高度：

将为问题1建立突水水流在巷道网络中的漫延模型，并用LaTeX格式表示相关数学公式。

问题1：突水水流漫延模型

1. 模型基础假设

根据题目描述，建立以下基础参数：

巷道矩形断面：宽度 $w = 4$ m，高度 $h = 3$ m
断面积： $\times h = 12$ m²
突水流量： $Q = 30$ m³/min = $0.5$ m³/s
初始水位： $h_0 = 0.1$ m

2. 水流传播机制

2.1 单一巷道中的水流传播

对于长度为 $L$ 的巷道段，水流传播遵循以下规律：

水流前锋速度：
$\frac{Q}{w \times h_0} = \frac{0.5}{4 \times 0.1} = 1.25 \text{ m/s}$

水流到达巷道末端的时间：
$tarrive=Lv=L1.25t_{arrive} = \frac{L}{v} = \frac{L}{1.25}$

2.2 巷道充水过程

当水流到达巷道末端后，该巷道开始充水。充水体积为：
$m³V_{tunnel} = L \times w \times h = L \times 4 \times 3 = 12L \text{ m³}$

巷道完全充满水的时间：
$tfull=tarrive+VtunnelQ=L1.25+12L0.5=L1.25+24Lt_{full} = t_{arrive} + \frac{V_{tunnel}}{Q} = \frac{L}{1.25} + \frac{12L}{0.5} = \frac{L}{1.25} + 24L$

2.3 节点分流规律

当水流到达分叉节点时，按以下规律分流：

设节点有 $n$ 个出口方向（包括水平巷道和下行巷道），则每个方向的流量为：
$Qi=Qn,i=1,2,…,nQ_i = \frac{Q}{n}, \quad i = 1,2,\ldots,n$

对于上行巷道，水流不能逆重力方向流动，因此：
$Q_{up} = 0$

3. 网络拓扑分析

3.1 巷道网络表示

将矿井巷道网络表示为有向图 $G = (V, E)$ ，其中：

$\{v_1, v_2, \ldots, v_n\}$ 为节点集合（端点）
$\{e_1, e_2, \ldots, e_m\}$ 为边集合（巷道）

每个节点 $v_i$ 的坐标为 $x_i, y_i, z_i)$ ，每条边 $e_{ij}$ 连接节点 $v_i$ 和 $v_j$ 。

3.2 巷道长度和坡度计算

巷道 $e_{ij}$ 的长度：
$Lij=(xj−xi)2+(yj−yi)2+(zj−zi)2L_{ij} = \sqrt{(x_j-x_i)^2 + (y_j-y_i)^2 + (z_j-z_i)^2}$

巷道坡度：
$θij=arctan⁡(zj−zi(xj−xi)2+(yj−yi)2)\theta_{ij} = \arctan\left(\frac{z_j-z_i}{\sqrt{(x_j-x_i)^2 + (y_j-y_i)^2}}\right)$

4. 水流传播算法

4.1 初始化

确定突水点位置，找到最近的巷道
我来帮您解决矿井突水水流漫延模型的第一个问题。首先需要建立水流在巷道网络中的传播模型，然后计算各个端点的水流到达时间和巷道充满水的时间。

import pandas as pd
import numpy as np
import networkx as nx
from collections import deque, defaultdict
import mathclass MineWaterFlowModel:def __init__(self, tunnel_width=4.0, tunnel_height=3.0, initial_water_height=0.1, flow_rate=30.0):"""初始化矿井水流模型tunnel_width: 巷道宽度(m)tunnel_height: 巷道高度(m) initial_water_height: 初始水位(m)flow_rate: 突水流量(m³/min)"""self.tunnel_width = tunnel_widthself.tunnel_height = tunnel_heightself.initial_water_height = initial_water_heightself.flow_rate = flow_rateself.tunnel_cross_section = tunnel_width * tunnel_height  # 巷道截面积def load_mine_data(self, points_file, tunnels_file):"""加载矿井数据"""# 读取端点数据points_df = pd.read_excel(points_file, sheet_name='端点')points_df.columns = ['Point_ID', 'X', 'Y', 'Z']# 读取巷道数据tunnels_df = pd.read_excel(tunnels_file, sheet_name='巷道')tunnels_df.columns = ['Tunnel_ID', 'Start_Point', 'End_Point']return points_df, tunnels_dfdef build_network_graph(self, points_df, tunnels_df):"""构建网络图"""G = nx.Graph()# 添加节点（端点）for _, row in points_df.iterrows():G.add_node(row['Point_ID'], x=row['X'], y=row['Y'], z=row['Z'])# 添加边（巷道）for _, row in tunnels_df.iterrows():start_id = row['Start_Point']end_id = row['End_Point']# 计算巷道长度和坡度start_pos = G.nodes[start_id]end_pos = G.nodes[end_id]length = math.sqrt((start_pos['x'] - end_pos['x'])**2 + (start_pos['y'] - end_pos['y'])**2 + (start_pos['z'] - end_pos['z'])**2)# 计算高程差（正值表示上行，负值表示下行）elevation_diff = end_pos['z'] - start_pos['z']slope = elevation_diff / length if length > 0 else 0G.add_edge(start_id, end_id, tunnel_id=row['Tunnel_ID'],length=length,slope=slope,elevation_diff=elevation_diff)return Gdef find_nearest_point(self, G, target_coords):"""找到最接近目标坐标的端点"""min_dist = float('inf')nearest_point = Nonefor node_id in G.nodes():node = G.nodes[node_id]dist = math.sqrt((node['x'] - target_coords[0])**2 + (node['y'] - target_coords[1])**2 + (node['z'] - target_coords[2])**2)if dist < min_dist:min_dist = distnearest_point = node_idreturn nearest_pointdef find_escape_path(self, G, start_point, end_point):"""找到从起点到终点的逃生路径"""start_id = self.find_nearest_point(G, start_point)end_id = self.find_nearest_point(G, end_point)try:path = nx.shortest_path(G, source=start_id, target=end_id, weight='length')return pathexcept nx.NetworkXNoPath:return None