洛谷 P3384 【模板】重链剖分/树链剖分-提高+/省选-
P3384 【模板】重链剖分/树链剖分
题目描述
如题,已知一棵包含 NNN 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
-
1 x y z,表示将树从 xxx 到 yyy 结点最短路径上所有节点的值都加上 zzz。 -
2 x y,表示求树从 xxx 到 yyy 结点最短路径上所有节点的值之和。 -
3 x z,表示将以 xxx 为根节点的子树内所有节点值都加上 zzz。 -
4 x,表示求以 xxx 为根节点的子树内所有节点值之和。
输入格式
第一行包含 444 个正整数 N,M,R,PN,M,R,PN,M,R,P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 NNN 个非负整数,分别依次表示各个节点上初始的数值。
接下来 N−1N-1N−1 行每行包含两个整数 x,yx,yx,y,表示点 xxx 和点 yyy 之间连有一条边(保证无环且连通)。
接下来 MMM 行每行包含若干个正整数,每行表示一个操作。
输出格式
输出包含若干行,分别依次表示每个操作 222 或操作 444 所得的结果(对 PPP 取模)。
输入输出样例 #1
输入 #1
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
输出 #1
2
21
说明/提示
【数据规模】
对于 30%30\%30% 的数据: 1≤N≤101 \leq N \leq 101≤N≤10,1≤M≤101 \leq M \leq 101≤M≤10;
对于 70%70\%70% 的数据: 1≤N≤1031 \leq N \leq {10}^31≤N≤103,1≤M≤1031 \leq M \leq {10}^31≤M≤103;
对于 100%100\%100% 的数据: 1≤N≤1051\le N \leq {10}^51≤N≤105,1≤M≤1051\le M \leq {10}^51≤M≤105,1≤R≤N1\le R\le N1≤R≤N,1≤P≤2301\le P \le 2^{30}1≤P≤230。所有输入的数均在 int 范围内。
【样例说明】
树的结构如下:
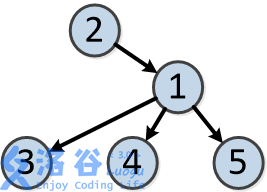
各个操作如下:
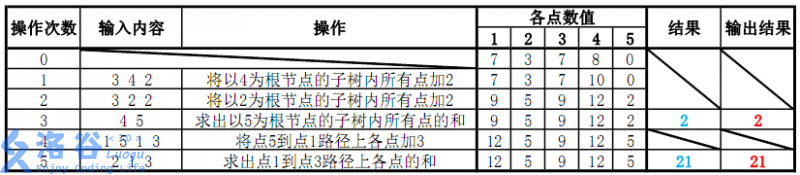
故输出应依次为 222 和 212121。
solution
思路: 节点和操作次数规模较大,不能逐个操作,应该批量处理。要完成批量处理,应该先将操作的点映射成若干个连续的区间
找到每个点的 dfn 序,每个子节点,先访问重链(节点最多的),则满足
- 1 子树的节点 dfn 连续
- 2 同一条重链的子节点连续。对于一条路径,可以分解为若干条重链的一段
具体做法: - 1 dfs 找到任意节点 u 的子节点数量 siz[u], 重链儿子 son[u], 父节点 fa[u], 深度 d[u]
- 2 dfs 按照先重儿子的顺序遍历,找到任意节点 u 的访问顺序 dfn[u],所在重链的顶端 top[u], 初始序 id[dfn[u]] = u
- 3 用线段树完成区间修改和查询操作
- 以x为根的子树dfn范围 [dfn[x], dfn[x] + siz[x] - 1]
- x->y路径的dfn范围 while(top[x] != top[y]) if(d[x] < d[y]) swap(x,y), [x, top[x]], x = fa[top[x]]
- if(d[x] < d[y]) swap(x,y) [x, y]
代码
#include <iostream>
#include "bit"
#include "vector"
#include "unordered_set"
#include "set"
#include "queue"
#include "algorithm"
#include "bitset"
#include "cstring"using namespace std;/** P3384 【模板】重链剖分/树链剖分* 题目大意:* 一棵 N 个结点的树,每个节点上包含一个数值,需要支持以下操作共M次 (1≤N,M≤10^5)。* 1 x y z,表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。* 2 x y,表示求树从 x 到 y 结点最短路径上所有节点的值之和。* 3 x z,表示将以 x 为根节点的子树内所有节点值都加上 z。* 4 x,表示求以 x 为根节点的子树内所有节点值之和。* 思路:节点和操作次数规模较大,不能逐个操作,应该批量处理。要完成批量处理,应该先将操作的点映射成若干个连续的区间* 找到每个点的 dfn 序,每个子节点,先访问重链(节点最多的),则满足* 1 子树的节点 dfn 连续* 2 同一条重链的子节点连续。对于一条路径,可以分解为若干条重链的一段* 具体做法:* 1 dfs 找到任意节点 u 的子节点数量 siz[u], 重链儿子 son[u], 父节点 fa[u], 深度 d[u]* 2 dfs 按照先重儿的顺序遍历,找到任意节点 u 的访问顺序 dfn[u],所在重链的顶端 top[u], 初始序 id[dfn[u]] = u* 3 用线段树完成区间修改和查询操作* 以x为根的子树dfn范围 [dfn[x], dfn[x] + siz[x] - 1]* x->y路径的dfn范围 while(top[x] != top[y]) if(d[x] < d[y])swap(x,y), [x, top[x]], x = fa[top[x]]* if(d[x] < d[y])swap(x,y) [x, y]*/typedef pair<int, int> pii;
typedef long long LL;const int N = 1e5 + 5;int n, m, R, P, val[N], fa[N], d[N], siz[N], son[N], dfn[N], top[N], id[N], t;
vector<int> e[N];void dfs(int u, int p) {fa[u] = p;d[u] = d[p] + 1;siz[u] = 1;int Max = -1;for (int v: e[u]) {if (v == p) continue;dfs(v, u);siz[u] += siz[v];if (siz[v] > Max) Max = siz[v], son[u] = v;}
}void dfs2(int u, int tp) {dfn[u] = ++t;top[u] = tp;id[t] = u;if (!son[u]) return;dfs2(son[u], tp);for (int v: e[u]) {if (v == fa[u] || v == son[u]) continue;dfs2(v, v);}
}LL tag[N << 2], sum[N << 2];void push_up(int rt) {sum[rt] = (sum[rt << 1] + sum[rt << 1 | 1]) % P;
}void push_down(int l, int r, int rt) {int mid = l + r >> 1;sum[rt << 1] = (sum[rt << 1] + tag[rt] * (mid - l + 1)) % P;sum[rt << 1 | 1] = (sum[rt << 1 | 1] + tag[rt] * (r - mid)) % P;tag[rt << 1] = (tag[rt << 1] + tag[rt]) % P;tag[rt << 1 | 1] = (tag[rt << 1 | 1] + tag[rt]) % P;tag[rt] = 0;
}void build(int l, int r, int rt) {if (l == r) {sum[rt] = val[id[l]] % P;return;}int mid = l + r >> 1;build(l, mid, rt << 1);build(mid + 1, r, rt << 1 | 1);push_up(rt);
}void update(int ll, int rr, int l, int r, int rt, int v) {if (ll <= l && r <= rr) {tag[rt] = (tag[rt] + v) % P;sum[rt] = (sum[rt] + v * (r - l + 1)) % P;return;}push_down(l, r, rt);int mid = l + r >> 1;if (mid >= ll) update(ll, rr, l, mid, rt << 1, v);if (mid < rr) update(ll, rr, mid + 1, r, rt << 1 | 1, v);push_up(rt);
}LL query(int ll, int rr, int l, int r, int rt) {if (ll <= l && r <= rr) return sum[rt];push_down(l, r, rt);int mid = l + r >> 1;LL ans = 0;if (mid >= ll) ans = (ans + query(ll, rr, l, mid, rt << 1)) % P;if (mid < rr) ans = (ans + query(ll, rr, mid + 1, r, rt << 1 | 1)) % P;return ans;
}int main() {cin >> n >> m >> R >> P;for (int i = 1; i <= n; i++) cin >> val[i];for (int i = 1, x, y; i < n; i++) {cin >> x >> y;e[x].push_back(y);e[y].push_back(x);}dfs(R, 0);dfs2(R, R);build(1, n, 1);for (int i = 1, op, x, y, z; i <= m; i++) {cin >> op >> x;LL s;switch (op) {case 1:cin >> y >> z;while (top[x] != top[y]) {if (d[top[x]] < d[top[y]]) swap(x, y);update(dfn[top[x]], dfn[x], 1, n, 1, z);x = fa[top[x]];}if (d[x] < d[y]) swap(x, y);update(dfn[y], dfn[x], 1, n, 1, z);break;case 2:cin >> y;s = 0;while (top[x] != top[y]) {if (d[top[x]] < d[top[y]]) swap(x, y);s += query(dfn[top[x]], dfn[x], 1, n, 1);s %= P;x = fa[top[x]];}if (d[x] < d[y]) swap(x, y);s += query(dfn[y], dfn[x], 1, n, 1), s %= P;cout << s << endl;break;case 3:cin >> z;update(dfn[x], dfn[x] + siz[x] - 1, 1, n, 1, z);break;default: // 4cout << query(dfn[x], dfn[x] + siz[x] - 1, 1, n, 1) << endl;}}return 0;
}
结果

