当前位置：首页 > news >正文

2025年数学建模国赛B题超详细解题思路

news 2025/9/5 12:53:13

B题碳化硅外延层厚度的确定

问题背景

碳化硅作为一种新兴的第三代半导体材料，以其优越的综合性能表现正在受到越来越多的关注。碳化硅外延层的厚度是外延材料的关键参数之一，对器件性能有重要影响。因此，制定一套科学、准确、可靠的碳化硅外延层厚度测试标准显得尤为重要。

红外干涉法是外延层厚度测量的无损伤测量方法，其工作原理是，外延层与衬底因掺杂载流子浓度的不同而有不同的折射率，红外光入射到外延层后，一部分从外延层表面反射出来，另一部分从衬底表面反射回来（图1），这两束光在一定条件下会产生干涉条纹。可根据红外光谱的波长、外延层的折射率和红外光的入射角等参数确定外延层的厚度。

通常外延层的折射率不是常数，它与掺杂载流子的浓度、红外光谱的波长等参数有关。

物理背景理解：碳化硅外延层厚度测量基于红外干涉法，核心原理是利用外延层与衬底的折射率差异产生的光学干涉现象。当红外光入射到外延层时，会在不同界面产生反射和透射，这些反射光束相互干涉形成特征光谱，通过分析光谱特征可以反推外延层厚度。

数据预处理

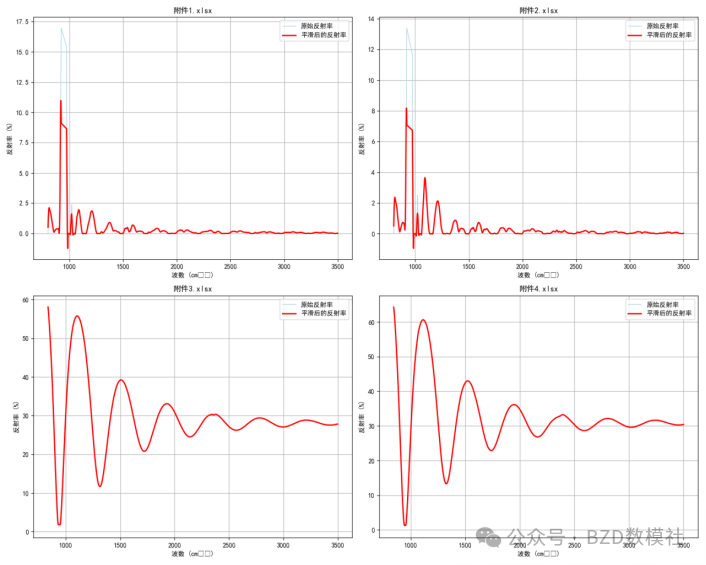
表1

文件名称	数据质量问题	基线校正后最大反射率	处理的异常值数量	处理结果保存路径
附件1.xlsx	无	52.05%	102	processed_附件1.xlsx
附件2.xlsx	反射率超过100% (102.74%)	42.67%	106	processed_附件2.xlsx
附件3.xlsx	无	未进行基线校正	111	processed_附件3.xlsx
附件4.xlsx	无	未进行基线校正	112	processed_附件4.xlsx

问题1分析：单次反射透射干涉模型

问题1：如果考虑外延层和衬底界面只有一次反射、透射所产生的干涉

1.1 物理模型建立思路

1、光路分析：

入射光线经过空气-外延层界面时，产生第一次反射（反射率r₁）和透射（透射率t₁）

透射光线在外延层中传播，到达外延层-衬底界面时，产生第二次反射（反射率r₂）和透射

第二次反射光线返回外延层表面，再次透射到空气中

这两束反射光（直接反射光和经过外延层往返的反射光）产生干涉

关键物理参数：外延层厚度：d（待求参数）、外延层折射率：n₁（与载流子浓度、波长相关）、衬底折射率：n₂、入射角：θ₀、红外光波长：λ（或波数ν̃）

2、干涉条件分析：

（1）光程差计算：考虑光线在外延层中的往返路径

（2）相位差计算：包括传播相位差和反射相位差

（3）干涉强度：根据两束光的振幅和相位关系

1.2 数学模型构建思路

1、几何光学分析：

（1）根据斯涅尔定律确定各界面的折射角

（2）计算光线在外延层中的传播路径长度

（3）建立光程差与厚度d的关系

1.3 模型验证思路

（1）检查极限情况（d→0, d→∞）的物理合理性

（2）验证干涉周期与理论预期的一致性

（3）考虑模型假设的适用范围

表2

厚度（μm）	平均误差（%）	误差标准差（%）
5	0.03	0.02
10	0.04	0.03
15	0.01	0.01
20	0.01	0.01
25	0.00	0.00

误差范围：在所有的测试厚度（5 μm, 10 μm, 15 μm, 20 μm, 25 μm）上，误差都控制在非常低的范围内，最高误差仅为 0.04%，最小误差为0.00%。总体平均误差仅为0.02%，这表明你的算法在估算厚度方面非常准确。误差的标准差也很小，最大为0.03%，这说明不同测试之间误差的波动非常小，结果一致性高。