当前位置：首页 > news >正文

笔记：卷积神经网络（CNN)

news 2025/9/4 10:37:48

1.卷积神经网络流程

2.模拟一个简单的卷积流程（输入到扫描）

3.提取图片特征

3.1. 把 RGB → 灰度图（数值矩阵）

3.2. 灰度图→张量→标准化

4.填充

4.1. 填充是什么/为什么

4.2. 常见填充方式

5.扫描

5.1. 卷积核的生成

5.2. 扫描时的运算

5.3. 卷积核的优化

5.4. 卷积核为什么不用2*2的，卷积核的大小会有什么影响？

6.池化

6.1. 池化是做什么

6.2. 池化历程

6.3. 池化边界不能够整除怎么办？

7.扁平化

7.1. 扁平是什么

8.全连接层运算

8.1. 局部感受野

8.2. 神经元的连接与参数

8.2.1. 局部连接但不共享参数（早期神经网络的思路）

8.2.2. 卷积层（局部连接 + 参数共享）

8.3. 偏置（bias）

8.4. 超参数和可学习参数

8.4.1. 人为设定（超参数，训练前就敲定)

8.4.2. 训练中学习（可学习参数）

8.4.3. 两类参数的关系

8.5. 深究池化的影响

8.6. 扁平化的作用

9. 小结

笔者作为仅有一小部分基础的情况下，前1-7阐述了基本定义，8通过串联和补缺成功对卷积神经网络有了相对的了解和理解。

1.卷积神经网络流程

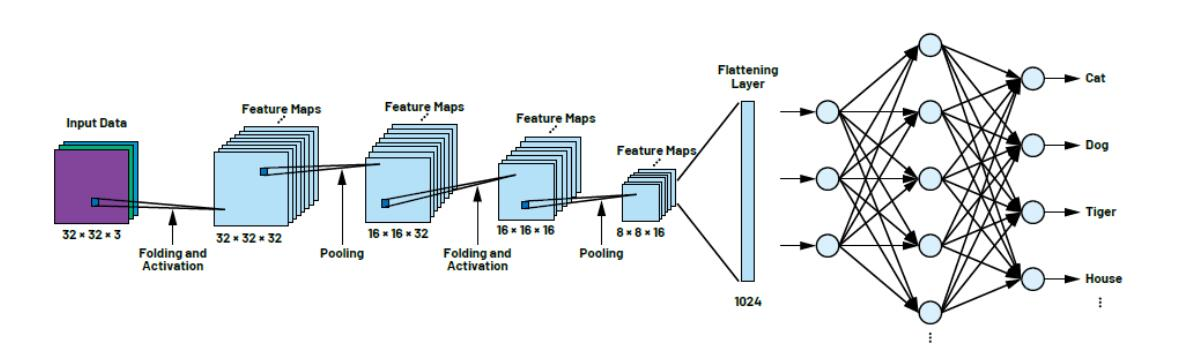
输入-->提取图片特征-->填充（可省略）-->扫描-->池化-->扁平化-->神经网络运算-->输出

2.模拟一个简单的卷积流程（输入到扫描）

数值参量：

灰度图/图像长 H 宽 W

卷积核边长 k

填充圈数 p

扫描步长 s

import numpy as npdef conv_out_hw(H, W, k, s=1, p=0, d=1):k_eff = d*(k-1)+1Ho = (H + 2*p - k_eff)//s + 1Wo = (W + 2*p - k_eff)//s + 1return Ho, Wodef scan_count_matrix(n=5, m=3, line=1, foot=1):H = W = np = lines = footk = m# 填充后的画布Hpad, Wpad = H+2*p, W+2*pcounts = np.zeros((Hpad, Wpad), dtype=int)# 只统计“核完整落入画布”的位置（VALID 滑动）for i in range(0, Hpad - k + 1, s):for j in range(0, Wpad - k + 1, s):counts[i:i+k, j:j+k] += 1return counts# 例子：5x5 输入, 3x3 卷积, p=1, s=1
H, W = 5, 5
k, p, s = 3, 1, 1
print("输出尺寸:", conv_out_hw(H, W, k, s, p))   # 期望 (5, 5)C = scan_count_matrix(n=H, m=k, line=p, foot=s)
print("填充后画布尺寸:", C.shape)                 # 7x7
print("扫描次数矩阵（每个像素被覆盖几次）:\n", C)

此程序输出了不同图像单元在填充后扫描的次数，如下图，显而易见，如果不经过填充，即p=0,边缘特征被扫描提取的次数即为有限，例如第一行，填充p=1时，分别为 4，6，6，6，4. p=0时，分别为 1，2，3，2，1

已经了解了大概流程，现在详述每个步骤。

3.提取图片特征

3.1. 把 RGB → 灰度图（数值矩阵）

灰度并不是简单求平均，更常用感知加权（人眼对 G 更敏感）：

BT.601（常见）
Y=0.299 R+0.587 G+0.114 B

BT.709（高清/现代）
Y=0.2126 R+0.7152 G+0.0722 B

这里的 R/G/B 通常指线性化后或已在 0~1 范围的值。

3.2. 灰度图→张量→标准化

常见的几种方式：

1. PIL + torchvision

2. OpenCV→PyTorch

3. 纯 NumPy（已经有灰度张量时手写权重）

4.填充

4.1. 填充是什么/为什么

在输入的边缘补像素，常见目的：

1. 保尺寸：卷积后高宽不变（便于残差/跳连）。

2. 边缘利用：让边界像素参与同等次数的卷积。

3. 控制输出尺寸：配合步长/空洞精确得到想要的大小。

4.2. 常见填充方式

1. zeros/constant：补 0（最常用），也可补常数 c。

2. reflect：镜像反射；

3. replicate：复制边缘。

4. circular：环绕（周期）。

5.扫描

5.1. 卷积核的生成

在深度学习里，卷积核（权重）不是手工写常数，而是可学习参数。

初始化（常见）：

Kaiming/He：适合 ReLU 家族

Xavier/Glorot：适合 tanh/线性

学习：前向算输出 → 计算损失 → 反向传播出梯度 → 用优化器更新

5.2. 扫描时的运算

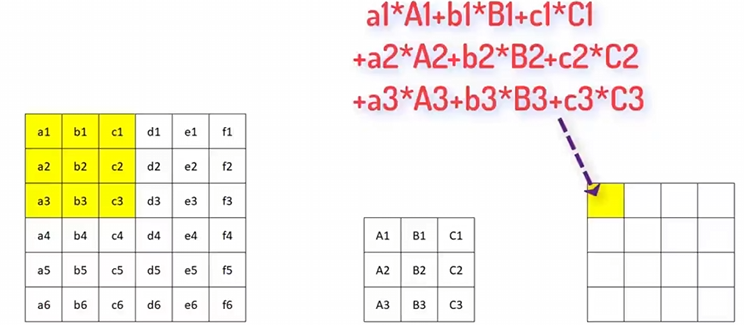
下图正是在演示一次卷积的“扫描运算”

左边黄框是输入特征图的一个 3×33\times33×3 局部窗口（元素 a1,b1,c1,…）。

中间是 3×3 卷积核（元素 A1,B1,C1,…）。

把两者对应元素相乘再求和（点积），得到右上角输出格子的数值：

5.3. 卷积核的优化

卷积核是一个可以优化学习的参量，可以理解为感知机中的weight权重，通过神经网络的前馈和计算损失，在经反向传播优化，虽然中间隔着池化和扁平化两个步骤，但是卷积核的梯度并不会被“池化”和“扁平化”隔断，反向传播会把梯度一层层按链式法则传回去；池化和扁平化只是中间的可微（或分段可微）算子，各自都有清晰的反传规则，梯度会穿过它们回到卷积层，从而更新卷积核。

使用 SGD、Adam 等优化器更新卷积核参数：

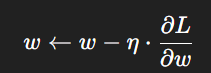
随着训练迭代，卷积核逐渐从随机数“长成”能够识别边缘、纹理、形状、语义的特征提取器。

5.4. 卷积核为什么不用2*2的，卷积核的大小会有什么影响？

答：首先，偶数核没有几何中心，保持尺寸（SAME）时只能“上0下1/左0右1”地填充，易产生半像素位移，残差/跳连更难对齐，累积后明显。2×2 不是不能用：最常见在 2×2 池化、或某些上采样。其次，卷积核以小核堆叠（3×3 为主）配合 BN/残差，训练更稳定。大核更像低频滤波，能更平滑/更全局，小核堆叠能逐步扩大 RF，同时保留细节与非线性表达。

6.池化

6.1. 池化是做什么

把特征图做下采样：抑制噪声、增强局部平移鲁棒性、降低计算量。相当于提取图中的主要信息来最大限度保留内容并提高效率。常见方法：

MaxPool：取窗口内最大值（保边缘/纹理更强）。

AvgPool：取窗口平均（更平滑）。

6.2. 池化历程

池化是一个提炼关键信息的过程，通过将池化单位中信息的聚合来减少计算。

假设一个6*6的灰度图经过3*3的卷积核扫描生成了如下4*4的矩阵。

1	1	1	2
2	3	1	1
3	4	1	1
1	2	1	1

我们采用2*2池化，并采用MaxPool方法形成一个2*2的矩阵如下：

3	2
4	1

6.3. 池化边界不能够整除怎么办？

上述4*4的矩阵恰好能被2*2的池化整除，但是如果不能整除，会采用两种常用方法：

1. VALID（默认）：不填充，尾部不满一窗的行/列丢掉（公式里的 floor）。

2.SAME / ceil 逻辑：输出按 ⌈H/sh⌉\lceil H/s_h\rceil⌈H/sh⌉，末尾不足一窗也输出（等价于“隐式填充”）。

PyTorch：ceil_mode=True；AvgPool 若不想让填充值稀释，设 count_include_pad=False。

或者先 pad 到能被步长整除再用 VALID 聚合（更可控，比如用 reflect/replicate）。

7.扁平化

7.1. 扁平是什么

定义：把卷积产生的多通道特征图（通常形状 [N, C, H, W]）在每个样本维度内拉直为一维向量（[N, C*H*W]），以便接到**全连接层（Linear/FC）**等“向量→向量”的模块。

本质：纯粹的重排/reshape操作，不引入参数；梯度在反向传播时原样传回相应位置（不会被截断）。

8.全连接层运算

8.1. 局部感受野

假设输入一个300*300的图像，下一层有10^4个神经元，如果采用全连接方式，那么一共有9*10^8个权重参数，而参数越多训练越难，因此引入局部感受野这一概念，让每一个神经元只链接图片中的其中一小部分，比如大小为4*4的范围，这个时候就只有1.6*10^5个权重参数了。

感受野（Receptive Field） 指的是：某个隐藏层神经元在输入层能看到的区域。

有效感受野（有区别于局部）的简单推到参见：笔记：深层卷积神经网络（CNN）中的有效感受野简单推导-CSDN博客

那每个神经元的局部感受野是怎么选择的呢？是随机还是有规则的？

首先我们要明确，在卷积层里，感受野是由卷积核大小决定的。卷积神经元不是随机挑区域，而是 有规则地滑动窗口。这是不是恰好就是第五部分扫描的内容！

那么第一个神经元看输入左上角的 4×4 像素，第二个神经元看右移 1 像素后的 4×4 区域，以此类推。最终这些神经元覆盖了整个图像，保证所有位置都被“扫描”到。

那如果扫描的次数远远小于神经元的个数，剩下的神经元获取谁的参数？

因此我们引入8.2. 详述神经元的参数分配。

8.2. 神经元的连接与参数

神经元的连接和参数设计两种情况：

8.2.1. 局部连接但不共享参数（早期神经网络的思路）

如果我们只在图像上“扫描”有限次，比如只放 5000 个窗口，但隐藏层设计了 10000 个神经元，那就会出现你说的情况：神经元数量 > 实际扫描位置数。

这时“多余”的神经元要么：

1. 没有输入（就闲置，相当于浪费）

2. 人工指定去看某些区域（比如多个神经元看同一个区域，但参数独立）。

所以在这种模式下，神经元数目和感受野数量需要人工设计，否则会出现资源浪费。

8.2.2. 卷积层（局部连接 + 参数共享）

CNN 里更常见的做法是：共享一组卷积核参数。

举例：一个 4×4 卷积核，就是 16 个参数（再加一个偏置）。这组参数会在整幅图像上“滑动”，每个滑动位置对应一个神经元的输出。如果滑动位置数量不够填满隐藏层的神经元个数 → 可以再增加卷积核的数量（即通道数，filters）。

比如你想要 10000 个神经元：假设滑动后得到 1000 个位置，那就需要 10 个不同的卷积核（1000×10 = 10000 个输出神经元）。

这样每个神经元都对应到某个位置 + 某个卷积核，不会出现“多余”神经元无事可做。

因此，有几个卷积核就扫描几次，就生成几个特征图。

那这些新增的卷积核是如何生成的，有参考内容还是单纯的随机？

卷积核里的权重（比如一个 3×3 卷积核就有 9 个参数 + 1 个偏置），在训练前并不是手工设计好的，而是 随机初始化的。没有预设“某个卷积核就负责边缘、某个卷积核就负责角点”，这些特征都是 训练过程中自动学到的。

常见的初始化策略，如5.1.中所讲这些初始化方法确保训练一开始卷积核不是“全 0”或“全一样”，避免网络学不动。

因为整个神经网络具有前馈传播，计算损失，反向传播，优化器优化组成的，只要卷积核初始化的不是特别的不方便学习，最后经过自主优化都能做到较大的识别概率。

这里要注意的是，卷积核和神经元是一对多的关系，多个神经元共同负责优化他们对应的那个卷积核。

8.3. 偏置（bias）

在8.2.2.中我们提到了，一个3*3的卷积核，是9个参数加一个偏置，那这个偏置的作用是什么？

笔记：人工神经网络-CSDN博客笔者在这篇文章给出过，卷积核的计算公式，原理同神经元的计算公式。

当卷积核在图像不同位置滑动时，权重 W和偏置 b 都是共享的；也就是说，这个卷积核在图像上所有位置的计算公式都一样，只是输入区域X不同；每个输出神经元的值都会加上 同一个偏置 b。

同卷积核的参数，偏置也是卷积核一步一步学出来的。

8.4. 超参数和可学习参数

在8.2.中我们谈到了为什么会出现多个卷积核，原因是不想空闲出一些神经元，提高利用率。但事实上，卷积核的大小和数量都是人为规定的，那什么是人为定下的参数，什么是机器自己优化的参数呢？我们引入超参数和可学习参数：

8.4.1. 人为设定（超参数，训练前就敲定)

卷积核大小 (kernel size)
- 例如 3×3、5×5、7×7
- 小核能提细节，大核感受野更大
卷积核个数 (number of filters)
- 决定输出特征图的“通道数”
- 多 → 特征更丰富，但参数多、计算量大
步幅 (stride)
- 卷积核每次移动的距离
- stride=1 → 保留细节；stride=2 → 特征图减半，更粗略
填充 (padding)
- 决定是否在输入边缘补零
- padding=0 → 图像越卷越小
- padding=“same” → 保持输入输出大小一致
网络层数、结构
- 几层卷积、是否加池化、全连接层大小
学习率、batch size、优化器类型
- 属于训练配置上的超参数