蒙特卡洛采样与粒子滤波算法学习

相关文章：
一文看懂蒙特卡洛采样方法
序列蒙特卡洛(SMC)与粒子滤波
五分钟入门马尔可夫链蒙特卡洛(MCMC)
浮光掠影之序列蒙特卡洛与粒子滤波

视频推导：
机器学习-白板推导系列(十六)-粒子滤波（Particle
Filter）

粒子滤波是序列蒙特卡洛方法最成功、最典型的应用实例。

前序数学基础

1. 状态空间模型：
   
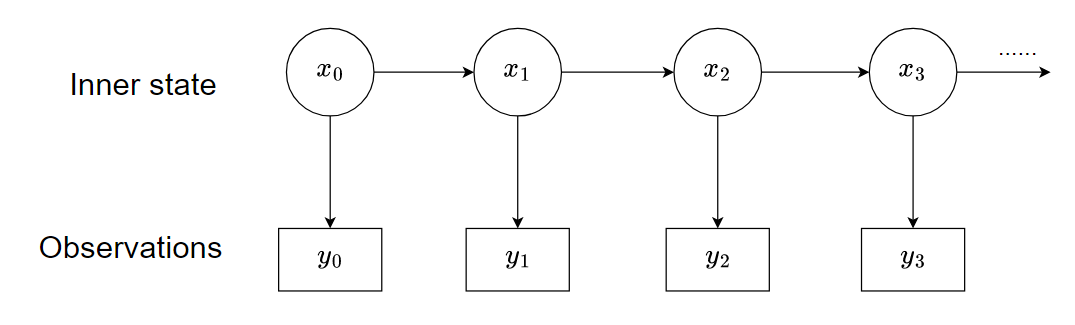
2. 概率的乘法法则（Multiplication Rule），有时也叫做链式法则（Chain Rule）。

• 两个变量的情况：
  P(A, B) = P(A | B) * P(B) = P(B | A) * P(A)
• 多个变量的情况（链式法则）：
  P(X1, X2, X3, …, Xn) = P(X1) * P(X2 | X1) * P(X3 | X1, X2) * … * P(Xn | X1, X2, …, Xn-1)
  联合概率被分解为：第一个变量的概率，乘以在第一个变量已知下第二个变量的概率，再乘以在前两个变量已知下第三个变量的概率，……，一直乘到在所有前面变量已知下最后一个变量的概率。

在状态空间模型中，我们经常要处理隐藏状态序列 x1, x2, …, xT 和观测序列 y1, y2, …, yT 的联合概率。

根据链式法则，先随意拆开：
P(x1:T, y1:T) = P(x1) * P(y1 | x1) * P(x2 | x1, y1) * P(y2 | x1, y1, x2) * … * P(xT | x1:T-1, y1:T-1) * P(yT | x1:T, y1:T-1)

然后，利用状态空间模型的假设来简化：

• 马尔可夫性：当前状态只依赖于前一个状态，即 P(xt | x1:t-1, y1:t-1) = P(xt | xt-1)

• 观测独立性：当前观测只依赖于当前状态，即 P(yt | x1:t, y1:t-1) = P(yt | xt)

将这些简化假设代入上面的链式展开，绝大多数条件项都被简化掉了：
P(x1:T, y1:T) = P(x1) * P(y1 | x1) * P(x2 | x1) * P(y2 | x2) * … * P(xT | xT-1) * P(yT | xT)

最终，一个极其复杂的联合概率被“拆”成了一系列非常简单的局部概率的乘积：
P(x1:T, y1:T) = P(x1) * [∏（从t=2到T） P(xt | xt-1)] * [∏（从t=1到T） P(yt | xt)]