AdaBoost（Adaptive Boosting，自适应提升算法）总结梳理

AdaBoost核心思想是 “让弱学习器变强”，核心是 “自适应加权”—— 通过调整样本权重让弱学习器关注难分样本，通过调整学习器权重让好的学习器更有话语权，最终加权融合成强学习器。它原理简单、易实现，同时也是处理简单任务、验证数据质量的实用工具。

总结一下：AdaBoost 先初始化所有样本权重，再迭代训练弱学习器（每次聚焦权重高的错分样本），并根据弱学习器性能分配权重，最终将所有弱学习器按权重加权组合，得到强学习器。

一、核心原理：“知错就改” 的自适应加权

AdaBoost 的本质是通过迭代训练多个 “弱学习器”（通常是简单决策树，即 “决策 stump”），并根据每个弱学习器的表现（误差）动态调整样本权重和学习器权重，最终将所有弱学习器加权融合成一个强学习器。

核心逻辑可拆解为两个 “自适应”：

1. 样本权重自适应：每次训练后，对 “上一轮被误分类的样本” 增加权重（让下一个弱学习器更关注这些难分样本），对 “正确分类的样本” 降低权重（减少不必要的关注）。
2. 学习器权重自适应：误差小的弱学习器（表现好）会被赋予更高的权重（在最终预测中更有话语权），误差大的弱学习器（表现差）权重更低（甚至被淘汰）。

其中，“弱学习器” 指 “性能略优于随机猜测” 的模型（比如二分类任务中，准确率 > 50% 的决策树），AdaBoost 通过 “集体智慧” 让多个弱学习器协同达到强学习器的效果。

二、完整流程：5 步迭代训练与融合

以二分类任务（标签为+1和-1）为例，假设训练样本集为{(x₁,y₁), (x₂,y₂), ..., (xₙ,yₙ)}，共迭代M次（训练M个弱学习器），流程如下：

1. 初始化：样本权重平均分配

第一次训练前，所有样本的权重相同（因为此时没有 “难分样本” 的信息）：

2. 迭代训练弱学习器（共 M 轮）

对每一轮m（从 1 到 M）：

• 步骤 2.1：基于当前样本权重训练弱学习器 hₘ
  用带权重的样本训练一个弱学习器（如决策 stump），目标是最小化 “加权分类误差”。
  加权误差定义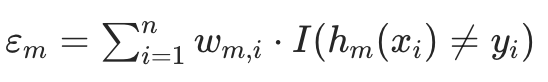：（I(·)是指示函数，括号内为真时取 1，否则取 0；即误差是 “被误分类样本的权重之和”）。

• 步骤 2.2：计算弱学习器 hₘ的权重 αₘ
  根据误差εₘ确定该弱学习器在最终融合中的 “话语权”，公式为：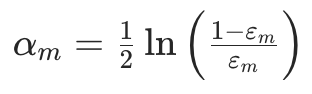

  • 若εₘ < 0.5（弱学习器略优于随机）：αₘ > 0，且εₘ越小，αₘ越大（表现好的学习器权重高）；
  • 若εₘ = 0.5（和随机一样）：αₘ = 0（该学习器无贡献，可跳过）；
  • 若εₘ > 0.5（比随机差）：αₘ < 0（实际中会避免这种情况，通常会重新训练弱学习器）。

• 步骤 2.3：更新样本权重（关键！自适应调整）
  为下一轮训练调整样本权重：让误分类样本权重增加，正确分类样本权重减少，公式为：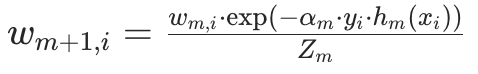

  

  其中：

  • Zₘ是 “归一化因子”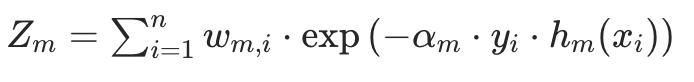：，确保更新后的权重总和为 1（满足概率分布）；
  • 若（正确分类）：，则exp(-αₘ) < 1，样本权重降低；
  • 若（误分类）：，则exp(αₘ) > 1，样本权重升高。

3. 融合所有弱学习器：加权投票

训练完M个弱学习器后，最终的强学习器H(x)是所有弱学习器的加权投票（二分类）：

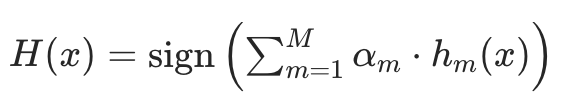
• sign(·)是符号函数：括号内结果为正，输出+1；为负，输出-1；
• 本质是 “让权重高的弱学习器（αₘ大）投的票更有分量”。

若为回归任务（标签是连续值），核心逻辑不变，仅细节调整：

• 弱学习器的误差用 “加权平方误差” 计算；
• 最终预测无需 sign 函数，直接加权求和即可。

三、核心作用：解决 “弱学习器泛化能力差” 的问题

AdaBoost 的核心价值是将多个简单、易训练但泛化能力弱的 “弱学习器”，组合成泛化能力强的 “强学习器”，具体作用场景包括：

1. 处理简单分类 / 回归任务
   无需复杂模型（如深度神经网络），用简单决策 stump 即可实现高精度预测，训练速度快、成本低（适合数据量不大、特征不复杂的场景）。

2. 作为 “基准模型” 验证效果
   在尝试复杂模型（如 XGBoost、LightGBM）前，先用 AdaBoost 验证数据的 “可学习性”—— 若 AdaBoost 效果极差，可能是数据质量（如标签错误、特征无关）问题，而非模型复杂度不足。

3. 特征重要性评估
   可通过 “弱学习器（如决策树）的分裂特征频率” 或 “特征对分类误差的贡献”，评估每个特征的重要性（辅助特征选择）。

4. 减少过拟合（相对弱学习器）
   单个弱学习器（如深度决策树）易过拟合，但 AdaBoost 通过多个弱学习器的 “投票”，降低了对单个样本的敏感度，泛化能力更强（但注意：若弱学习器数量过多，AdaBoost 也可能过拟合）。

四、一些记录

1. 为什么弱学习器通常选 “决策 stump”？

决策 stump 是 “深度为 1 的决策树”（仅一个分裂节点，分左右两个叶子），选择它的原因：

• 简单易训练：仅需遍历所有特征和可能的分裂点，找到 “加权误差最小” 的分裂方式，计算成本低；
• 避免 “强学习器垄断”：若用强学习器（如深度决策树），单个学习器已能拟合大部分数据，后续迭代的学习器贡献小，失去 “Boosting” 的意义。

2. 如何判断迭代次数 M（弱学习器数量）？

M 是 AdaBoost 的关键超参数，需通过 “验证集” 调优：

• M 过小：弱学习器数量不足，模型欠拟合（无法充分学习数据规律）；
• M 过大：模型可能过拟合（过度关注训练集的噪声样本，泛化能力下降）；
• 常用策略：设置较大的 M，结合 “早停”（当验证集误差连续多轮上升时，停止迭代）。

3. AdaBoost 的局限性

• 对异常值 / 噪声敏感：异常值易被误分类，导致其权重不断升高，后续弱学习器过度关注异常值，最终影响整体预测效果（这也是 XGBoost/LightGBM 加入 “二阶导数正则化” 的原因之一）。
• 不适合高维稀疏数据：当特征维度极高（如文本 One-Hot 编码），决策 stump 难以找到有效分裂特征，效果不如 SVM、神经网络。
• 无法并行训练：迭代过程依赖上一轮的样本权重，弱学习器必须 “串行训练”（而 XGBoost/LightGBM 支持部分并行，速度更快）。

4. AdaBoost 与其他 Boosting 模型的核心区别

模型	弱学习器权重	样本权重更新逻辑	并行能力	对异常值敏感度
AdaBoost	仅依赖误差 εₘ	基于 “分类对错” 调整权重	无（串行）	高（易受影响）
XGBoost	结合误差 + 正则	基于梯度和二阶导数调整	部分并行	低（有正则化）
LightGBM	结合误差 + 正则	基于梯度和二阶导数调整	高效并行	低（有正则化）