MATLAB矩阵及其运算(四)矩阵的运算及操作
一、矩阵的运算
MATLAB的运算符分为算术运算符、关系运算符和逻辑运算符三大类别。
1.1 算术运算符
MATLAB的算术运算符如下表:
| 符号 | 功能 |
| + | 相加 |
| - | 相减 |
| * | 矩阵相乘 |
| .* | 数组相乘 |
| ^ | 矩阵乘方 |
| .^ | 数组乘方 |
| / | 左除 |
| \ | 右除 |
| ./ | 数组左除 |
| .\ | 数组右除 |
需注意的是,乘法、除法的对象为矩阵时,表示矩阵的乘除,而.*和./表示数组中对应元素的乘和除。
例:矩阵的乘法运算。
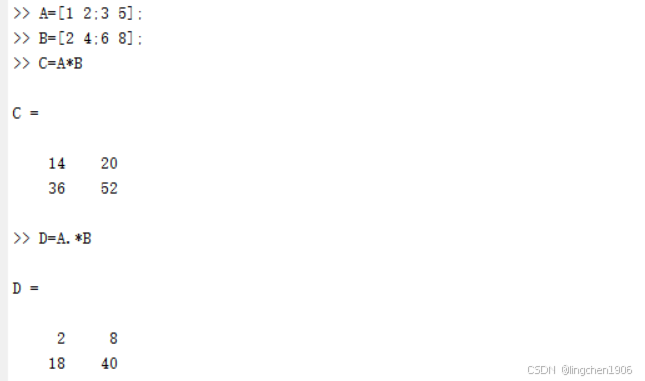
另外,左除、右除代表的含义也不同。
(1)对象为标量的时候,被除数的位置不同。
例:标量的左除和右除。
左除运算:

右除运算:

右除的分母在右边,左除的分母在左边。
(2)对象为矩阵的时候,代表的含义不同。
例:矩阵的左除和右除。

矩阵的左除是以左边的矩阵为除数,右除是以右边的矩阵为除数,因此得到的结果不一样。
1.2 关系运算符
MATLAB提供了6种关系运算符,其结果返回值为1或者0,分别表示运算关系是否成立。关系运算符如下表:
| 运算符 | 功能 |
| < | 小于 |
| <= | 小于等于 |
| > | 大于 |
| >= | 大于等于 |
| == | 等于 |
| ~= | 不等于 |
关系运算符通常用于程序的流程控制,常与if,while,for,switch等控制命令一起使用。
例:设矩阵A=[4 3 -5],B=[4 5 -8],比较两者的大小。
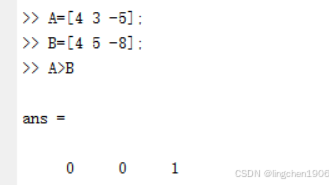
1.3 逻辑运算符
MATLAB提供了4种逻辑运算符,其结果返回值为1或0,表示一个逻辑量,即“真”或“假”。逻辑运算符如下表:
| 运算符 | 功能 |
| & | 与 |
| | | 或 |
| ~ | 非 |
| xor | 异或 |
例:设矩阵a=[1 3 9 - 8 5 6],判断矩阵a中大于3且小于7的元素。

二、矩阵的其他运算符
MATLAB的矩阵运算符非常丰富,能够满足各种运算需求,矩阵的其他运算符见下表:
| 符号 | 功能 |
| A' | 转置 |
| reshape(A,n,m) | 重新排列,保证重构后的新矩阵的元素与A一致 |
| rank(A) | 求秩 |
| det(A) | 矩阵行列式 |
| inv(A) | 矩阵求逆 |
2.1 转置
转置是将矩阵的行转成列,列转成行。
例:将矩阵转置。

2.2 重新排列
重新排列后的新矩阵,必须保证重构后的新矩阵的元素与A一致,两者行、列、维数相等。

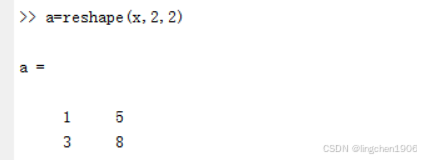
2.3 求秩
在线性代数中,一个矩阵A的列秩是A的线性独立(线性不相关)的纵列的极大数目。类似地,行秩是A的线性无关的横行的极大数目。也就是说,如果把矩阵看成是一个个行向量或者列向量,秩就是这些行向量或者列向量的秩,也就是极大无关组中所含向量的个数。
例:求矩阵的秩。

矩阵A为满秩矩阵(秩等于矩阵的行数(或列数,因为它是方阵)。
因为矩阵B中,第一行与第二行线性相关,故矩阵B的秩为2。
不满秩矩阵被称为奇异矩阵,其行列式一定等于0。
矩阵的秩是矩阵中线性无关的行(或列)向量的最大数量,计算方法主要有以下几种,适用于不同场景:
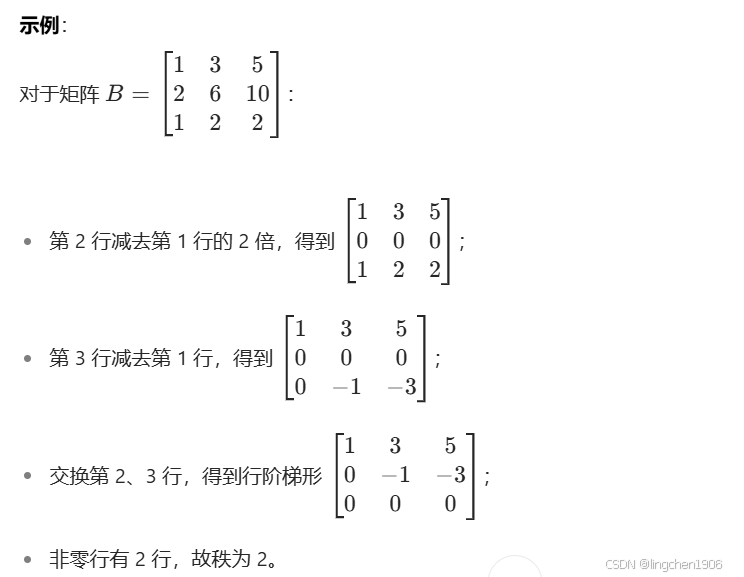
方法 1:通过行最简形(行阶梯形)计算
这是最常用的方法,步骤如下:
- 初等行变换:对矩阵进行初等行变换(交换两行、某行乘非零常数、某行加另一行的倍数),将矩阵化为行阶梯形矩阵(Row Echelon Form)。
- 数非零行:行阶梯形矩阵中非零行的数量即为矩阵的秩。
方法 2:通过行列式判断(仅适用于方阵)
对于n×n的方阵:
- 若行列式不为 0,则矩阵满秩(秩 = n)。
- 若行列式为 0,则秩 < n,需进一步判断(例如计算其 n-1阶子式是否非零,直至找到最高阶非零子式)。
示例: 3 阶矩阵 A 的行列式 det(A)不等于 0→ 秩为 3;
3 阶矩阵 B 的行列式 det(B) = 0,且存在 2 阶子式非零 → 秩为 2。
方法 3:通过向量组的线性相关性
- 把矩阵的行(或列)视为向量,构成行(或列)向量组。
- 求该向量组中线性无关向量的最大个数,即为矩阵的秩。

方法 4:用软件计算(实际应用中)
在 MATLAB、Python 等工具中,可直接调用函数:
- MATLAB:
rank(A) - Python(NumPy):
np.linalg.matrix_rank(A)
import numpy as np
A = np.array([[1,3,8], [2,4,6], [7,8,9]])
print(np.linalg.matrix_rank(A)) # 输出3关键结论
- 矩阵的秩 = 行秩 = 列秩(行秩与列秩相等)。
- 秩的范围:\(0 \leq \text{秩}(A) \leq \min(\text{行数}, \text{列数})\)。
- 初等变换不改变矩阵的秩(这是行阶梯形方法的理论基础)。
实际计算时,行阶梯形方法是最直观且通用的选择,尤其适合手动计算;软件工具则适合处理高阶矩阵。
2.4 矩阵行列式
行列式的计算方法根据矩阵阶数的不同而有所区别,以下是几种常用的计算方法,从低阶到高阶逐步介绍:

![]()

高阶行列式(n≥4)
高阶行列式计算较复杂,通常结合以下技巧简化:
方法 :初等行变换(化为上三角矩阵)
利用行列式的性质,通过初等行变换将矩阵化为上三角矩阵(主对角线下方元素全为 0),此时行列式等于主对角线元素的乘积。
行列式性质:
- 交换两行,行列式变号;
- 某行乘常数 k,行列式变为原来的 k 倍;
- 某行加另一行的倍数,行列式不变。

用软件计算(高效便捷)
在实际应用中,高阶行列式可通过工具快速计算:
- MATLAB:
det(A) - Python(NumPy):
np.linalg.det(A)
import numpy as np
A = np.array([[1, 2], [3, 4]])
print(np.linalg.det(A)) # 输出 -2.0总结
- 低阶行列式(2-3 阶):直接用公式或对角线法则。
- 高阶行列式:优先通过初等行变换化为上三角矩阵,或按零元素多的行 / 列展开。
- 实际应用:借助软件工具高效计算,避免手动计算出错。
行列式的核心意义在于判断矩阵是否可逆(行列式非零则可逆),以及求解线性方程组等场景。
矩阵行列式的调用命令是det。
例:求矩阵的行列式。
(1)不满秩的情况。
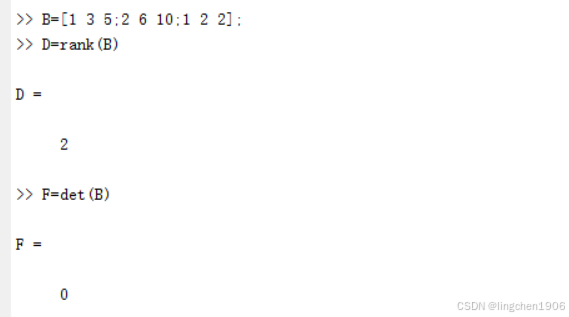
(2)满秩的情况。

2.5 矩阵求逆
一个矩阵具有逆矩阵,必须满足相应的条件。矩阵的逆矩阵存在的充要条件为:
(1)矩阵为满秩矩阵;
(2)矩阵的行列式不等于零;
(3)矩阵必须为方阵。
例:求矩阵的逆。

假如矩阵为奇异矩阵(不满秩),则其逆矩阵不存在。
例:求矩阵的逆。

2.6 矩阵的翻转与旋转
矩阵的翻转与旋转命令如下表:
| 命令 | 功能 |
| fliplr | 矩阵左右翻转 |
| flipud | 矩阵上下翻转 |
| flipdim | 矩阵的第n维翻转 |
| Rot90 | 矩阵逆时针旋转90度 |
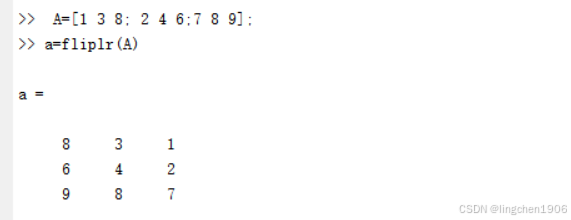

flipdim 函数的作用是沿指定维度翻转矩阵,它必须接收两个输入参数:
- 第一个参数是要翻转的矩阵(如变量
A) - 第二个参数是指定的翻转维度(1 表示沿行方向翻转,2 表示沿列方向翻转)
c = flipdim(A, 1); % 沿第1维度(行方向)翻转矩阵A
% 或
c = flipdim(A, 2); % 沿第2维度(列方向)翻转矩阵A在较新的 MATLAB 版本中,推荐使用更直观的 flip 函数替代 flipdim,用法类似:flip(A, 1) 或 flip(A, 2)。

2.7 矩阵的提取与合并
矩阵的提取主要分为两种形式:
一种使用函数提取;另一种使用冒号表达式提取。
函数diag实现矩阵对角元素的提取。
其调用格式如下:
(1)diag(x):
当输入x为矩阵的时候,输出结果为提取主对角线的元素形成的列向量。
当输入x为向量时,输出结果为以x为主对角线的对角矩阵。
(2)diag(x,k):
当输入x为矩阵的时候,输出结果为以x作为第k条对角线形成的列向量。
当输入x为向量的时候,输出结果为以x作为第k条对角线的对角矩阵。
例:矩阵的提取。
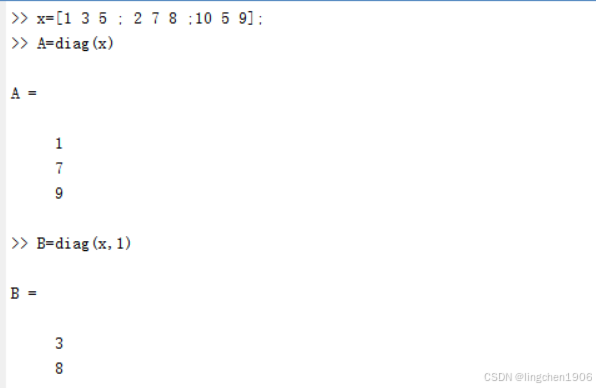
提取x中的第一条对角线元素形成向量输出。
例:向量的提取。


2.8 冒号“:”的使用
在MATLAB中,冒号表示全部的含义,除了用于形成等差数组,还能用于矩阵元素的提取。
例:冒号功能的使用示例。
已知矩阵
M=[1 5 6 ;9 8 7 ;2 90 10]
观察以下命令作用的结果。

显示矩阵M第一列的全部元素。

显示矩阵M第2行和第3行的全部元素
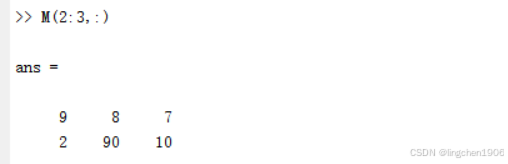
显示矩阵M第1行、第2行的第1列元素

显示矩阵M第4个位置的元素。

显示矩阵M第1个到第4个位置的元素

即当矩阵的括号里无逗号的时候,里面的元素表示位置。
M(a):a表示位置,M(3)表示第三个位置的元素。
M(1:5):表示提取第1个到第5个位置对应的元素。
有逗号的时候,逗号之前是行,之后是列,“:”表示全部。
M(1,6):表示提取第1行、第6列的元素
M(1:2,:)表示提取第1行、第2行的所有元素。
M(:,2:4:6)表示提取第2,4 6列的所有元素。
M(:,[1 3 4])表示提取第1,3,4列的所有元素。
M(:,[2 3])=[ ]表示删除第2 ,3列的所有元素。
2.9 矩阵的和并
将小矩阵合并成大矩阵的操作,主要利用分号和逗号表达式来完成。
例:已知A=[1 3 ;5 6],B= [7 8],C=[100 200 8]',将A与B合并成3行2列得到E矩阵,再将E与C合并成3行3列的矩阵。


