Ceres学习笔记

1. Ceres 是什么？能解决什么问题？

Ceres Solver 专用于解决非线性最小二乘问题。这类问题形式如下：

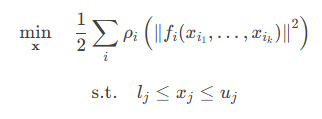
• 代价函数（CostFunction） f_i(…)： 这是我们定义的核心，它计算残差。例如，在曲线拟合中，它就是 观测值 - 预测值。
• 参数块（ParameterBlock） x_{i_1}, …, x_{i_k}： 我们要优化的变量。例如，曲线 y = e^{mx + c} 中的参数 m 和 c。
• 损失函数（LossFunction） ρ_i(…)： 一个核函数，用于减少异常值（Outliers）对整体解的影响（例如 HuberLoss）。
• 约束（Constraints） l_j \leq x_j \leq u_j： 变量的边界约束。

Ceres 的工作就是找到一组参数，使得所有残差的平方和（经过损失函数调整后）最小。

公式组成部分详解

1. 目标函数
   ${\min }_{\mathbf{x}}$：表示对参数向量 $\mathbf{x}$ 进行最小化优化
   $\frac{1}{2}$：缩放因子，使求导后形式更简洁
   ${\sum }_i$：对所有观测值或残差项求和
   ${\rho }_i$：损失函数（核函数），用于减少异常值的影响
   $|f_{}$