LeetCode Hot 100 Python (61~70)
分割回文串:中等
给你一个字符串 s,请你将 s 分割成一些 子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
| 示例 | 1 | 2 |
| 输入 | s = "aab" | s = "a" |
| 输出 | [["a","a","b"],["aa","b"]] | [["a"]] |
法一:输入的视角(逗号选或不选)
假设每对相邻字符之间有个逗号,那么就看每个逗号是选还是不选。
也可以理解成:是否要把 s[i] 当成分割出的子串的最后一个字符。注意 s[n−1] 一定是最后一个字符,一定要选。
class Solution:def partition(self, s: str) -> List[List[str]]:n = len(s)ans = []path = []# 考虑 i 后面的逗号怎么选# start 表示当前这段回文子串的开始位置def dfs(i: int, start: int) -> None:if i == n: # s 分割完毕ans.append(path.copy()) # 复制 pathreturn# 不选 i 和 i+1 之间的逗号(i=n-1 时一定要选)if i < n - 1:# 考虑 i+1 后面的逗号怎么选dfs(i + 1, start)# 选 i 和 i+1 之间的逗号(把 s[i] 作为子串的最后一个字符)t = s[start: i + 1]if t == t[::-1]: # 判断是否回文path.append(t)# 考虑 i+1 后面的逗号怎么选# start=i+1 表示下一个子串从 i+1 开始dfs(i + 1, i + 1)path.pop() # 恢复现场dfs(0, 0)

法二:答案的视角(枚举子串结束位置)
class Solution:def partition(self, s: str) -> List[List[str]]:n = len(s)ans = []path = []# 考虑 s[i:] 怎么分割def dfs(i: int) -> None:if i == n: # s 分割完毕ans.append(path.copy()) # 复制 pathreturnfor j in range(i, n): # 枚举子串的结束位置t = s[i: j + 1] # 分割出子串 tif t == t[::-1]: # 判断 t 是不是回文串path.append(t)# 考虑剩余的 s[j+1:] 怎么分割dfs(j + 1)path.pop() # 恢复现场dfs(0)return ans

N皇后:困难
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
| 示例 | 1 | 2 |
| 输入 | n = 4 | n = 1 |
| 输出 | [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] | [["Q"]] |
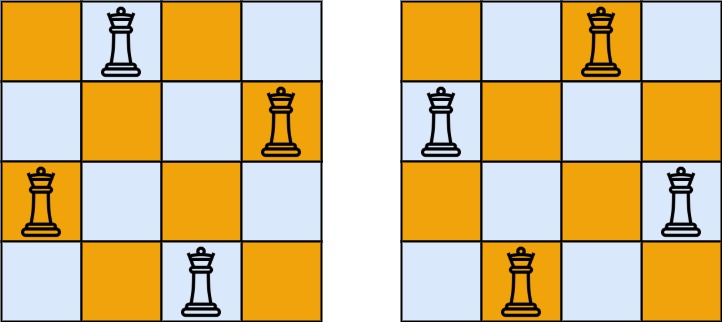
| 解释 | 如上图所示,4 皇后问题存在两个不同的解法。 | |
|
|
排列型回溯:
本题和 46. 全排列 的关系是什么?由于每行恰好放一个皇后,记录每行的皇后放在哪一列,可以得到一个 [0,n−1] 的排列 queens。示例 1 的两个图,分别对应排列 [1,3,0,2] 和 [2,0,3,1]。所以我们本质上是在枚举列号的全排列。
如何 O(1) 判断两个皇后互相攻击?由于我们保证了每行每列恰好放一个皇后,所以只需检查斜方向。对于 ↗ 方向的格子,行号加列号是不变的。对于 ↖ 方向的格子,行号减列号是不变的。如果两个皇后,行号加列号相同,或者行号减列号相同,那么这两个皇后互相攻击。
如何 O(1) 判断当前位置被之前放置的某个皇后攻击到?额外用两个数组 diag1和 diag2分别标记之前放置的皇后的行号加列号,以及行号减列号。如果当前位置的行号加列号在diag1中(标记为 true),或者当前位置的行号减列号在diag2中(标记为 true),那么当前位置被之前放置的皇后攻击到,不能放皇后。
class Solution:def solveNQueens(self, n: int) -> List[List[str]]:ans = []queens = [0] * n # 皇后放在 (r,queens[r])col = [False] * ndiag1 = [False] * (n * 2 - 1)diag2 = [False] * (n * 2 - 1)def dfs(r: int) -> None:if r == n:ans.append(['.' * c + 'Q' + '.' * (n - 1 - c) for c in queens])return# 在 (r,c) 放皇后for c, ok in enumerate(col):if not ok and not diag1[r + c] and not diag2[r - c]: # 判断能否放皇后queens[r] = c # 直接覆盖,无需恢复现场col[c] = diag1[r + c] = diag2[r - c] = True # 皇后占用了 c 列和两条斜线dfs(r + 1)col[c] = diag1[r + c] = diag2[r - c] = False # 恢复现场dfs(0)return ans

A000170 - OEIS
搜索插入位置:简单
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
| 1 | 2 | 3 | |
| 输入 | nums = [1,3,5,6], target = 5 | nums = [1,3,5,6], target = 2 | nums = [1,3,5,6], target = 7 |
| 输出 | 2 | 1 | 4 |
题意概括
返回 nums 中的第一个(最左边的)大于或等于 target 的数的下标。如果所有数都小于 target,返回 nums 的长度。
下面的代码包含闭区间、左闭右开区间和开区间三种写法。
# lower_bound 返回最小的满足 nums[i] >= target 的 i
# 如果数组为空,或者所有数都 < target,则返回 len(nums)
# 要求 nums 是非递减的,即 nums[i] <= nums[i + 1]# 闭区间写法
def lower_bound(nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1 # 闭区间 [left, right]while left <= right: # 区间不为空# 循环不变量:# nums[left-1] < target# nums[right+1] >= targetmid = (left + right) // 2if nums[mid] < target:left = mid + 1 # 范围缩小到 [mid+1, right]else:right = mid - 1 # 范围缩小到 [left, mid-1]return left# 左闭右开区间写法
def lower_bound2(nums: List[int], target: int) -> int:left = 0right = len(nums) # 左闭右开区间 [left, right)while left < right: # 区间不为空# 循环不变量:# nums[left-1] < target# nums[right] >= targetmid = (left + right) // 2if nums[mid] < target:left = mid + 1 # 范围缩小到 [mid+1, right)else:right = mid # 范围缩小到 [left, mid)return left # 或者 right# 开区间写法
def lower_bound3(nums: List[int], target: int) -> int:left, right = -1, len(nums) # 开区间 (left, right)while left + 1 < right: # 区间不为空mid = (left + right) // 2# 循环不变量:# nums[left] < target# nums[right] >= targetif nums[mid] < target:left = mid # 范围缩小到 (mid, right)else:right = mid # 范围缩小到 (left, mid)return rightclass Solution:def searchInsert(self, nums: List[int], target: int) -> int:return lower_bound(nums, target) # 选择其中一种写法即可
| 时间复杂度 | 空间复杂度 |
| O(log n) | O(1) |
| 其中 n 为 nums 的长度 | 仅用到若干额外变量 |
为什么不在二分的过程中,找到 target 就立刻返回?这种写法适用范围很窄。在有多个等于 target 的数的情况下,如果在二分的过程中立刻返回,我们得到的可能不是第一个等于 target 的数的下标。为什么返回第一个等于 target 的数的下标更好呢?因为这可以解决更复杂的题目,比如给你一个有序数组 [1,1,3,3,3,3,5],让你计算有多少个数小于 3。我们可以二分查找第一个等于 3 的数的下标 2,那么下标小于 2 的数就是元素值小于 3 的数,这有 2 个。对比可以发现,如果在二分中途就立刻返回,我们不一定找到的是第一个等于 3 的数的下标,所以不一定能算出正确答案 2。
为什么代码没有特判所有数都小于 target 的情况?如果所有数都小于 target,那么循环中更新的只有 left,无论下面哪种二分写法,最后都一定会返回数组长度,所以无需特判这种情况。
如果所有数都大于 target 呢?代码会返回 0。
是否需要特判 nums[mid]=target 的情况?可以,但没必要。
搜索二维矩阵:中等
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 tr