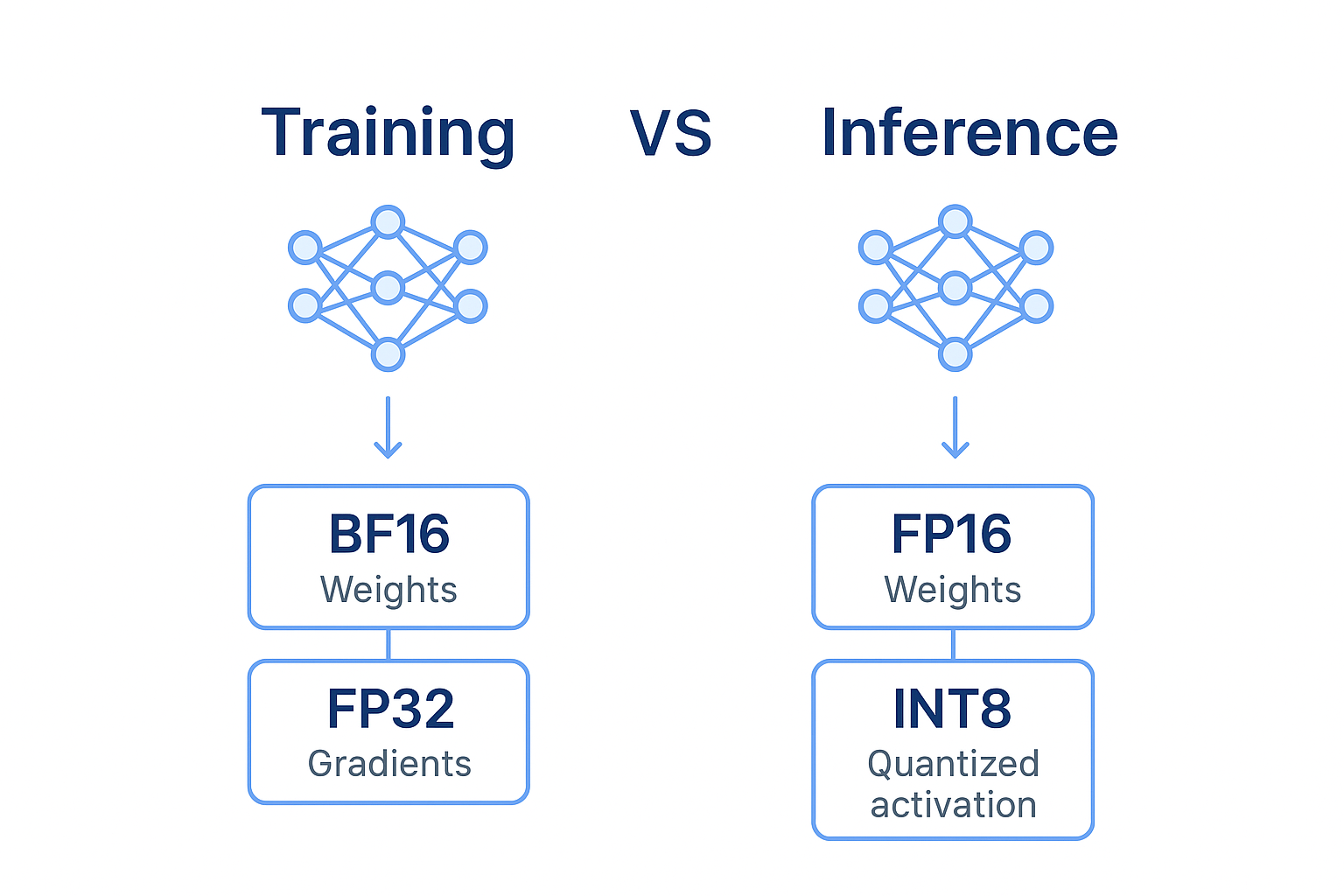
【无标题】训练、推理适用的数据类型
在深度学习中,浮点数表示格式主要用于表示模型权重、激活值和梯度,影响计算精度、显存占用和训练/推理速度。常见的浮点数格式如下:
1️⃣ FP32(单精度浮点)
位宽:32 位
结构:1 位符号 + 8 位指数 + 23 位尾数
用途:默认训练和推理精度
特点:
精度高,数值稳定
显存占用大,计算相对慢
2️⃣ FP16(半精度浮点)
位宽:16 位
结构:1 位符号 + 5 位指数 + 10 位尾数
用途:训练加速、推理
特点:
显存占用减半,计算更快
容易溢出或下溢,需要 loss scaling 处理
NVIDIA GPU Tensor Core 支持 FP16 运算
3️⃣ BF16(Brain Floating Point)
位宽:16 位
结构:1 位符号 + 8 位指数 + 7 位尾数
用途:大模型训练、混合精度训练
特点:
指数范围与 FP32 一致,数值范围大
尾数精度较低,但训练稳定性好
支持混合精度训练,TensorFlow / PyTorch 都可用
4️⃣ Mixed Precision(混合精度)
思路:
权重和激活使用 FP16 / BF16
梯度累加使用 FP32
优点:节省显存,提高训练速度,同时保持数值稳定性
工具:
PyTorch: torch.cuda.amp
TensorFlow: mixed_precision
5️⃣ INT8 / INT4(整数量化)
用途:推理加速,减少显存
特点:
INT8 / INT4 权重和激活表示
需要量化校准
对训练不适用,精度可能略有下降
总结对比
| 类型 | 位宽 | 指数 | 尾数 | 优点 | 缺点 |
|---|---|---|---|---|---|
| FP32 | 32 | 8 | 23 | 精度高,数值稳定 | 显存大,计算慢 |
| FP16 | 16 | 5 | 10 | 显存省,计算快 | 易溢出,需要 loss scaling |
| BF16 | 16 | 8 | 7 | 数值范围大,训练稳定 | 尾数精度低 |
| INT8 | 8 | - | - | 推理快,显存小 | 训练不适用 |
| INT4 | 4 | - | - | 超低显存,速度快 | 精度损失大 |
💡 经验建议:
训练大模型 → BF16 + FP32 梯度
训练中小模型 / 推理 → FP16 + mixed precision
部署推理 → INT8 / INT4