当前位置：首页 > news >正文

机器学习入门，非线性模型的预测方法之多项式

news 2025/9/2 12:53:10

import numpy as np
import matplotlib.pyplot as plt# 生成示例数据
def generate_sample_data(n_samples=100, noise=0.1, degree=2):"""生成多项式回归示例数据y = 0.5x² + 1.5x + 2 + 噪声"""np.random.seed(42)X = 4 * np.random.rand(n_samples, 1) - 2  # 生成-2到2之间的值y = 0.5 * X**2 + 1.5 * X + 2 + noise * np.random.randn(n_samples, 1)return X, y# 创建多项式特征
def create_polynomial_features(X, degree=2):"""将特征转换为多项式特征例如: degree=2时，将[x]转换为[1, x, x²]"""X_poly = np.ones((X.shape[0], 1))  # 添加偏置项for d in range(1, degree + 1):X_poly = np.c_[X_poly, X**d]return X_poly# 计算带有L2正则化的损失函数
def compute_loss(X, y, theta, lambda_):"""计算带有L2正则化的均方误差损失"""m = len(y)predictions = X.dot(theta)mse = (1 / (2 * m)) * np.sum((predictions - y) ** 2)l2_penalty = (lambda_ / (2 * m)) * np.sum(theta[1:] ** 2)  # 不对偏置项正则化return mse + l2_penalty# 计算梯度
def compute_gradient(X, y, theta, lambda_):"""计算带有L2正则化的梯度"""m = len(y)predictions = X.dot(theta)errors = predictions - ygradient = (1 / m) * X.T.dot(errors)# 对非偏置项添加L2正则化梯度gradient[1:] = gradient[1:] + (lambda_ / m) * theta[1:]return gradient# 梯度下降优化
def gradient_descent(X, y, theta, alpha, lambda_, iterations):"""执行带有L2正则化的梯度下降"""m = len(y)loss_history = []for i in range(iterations):# 计算梯度grad = compute_gradient(X, y, theta, lambda_)# 更新参数theta = theta - alpha * grad# 记录损失loss = compute_loss(X, y, theta, lambda_)loss_history.append(loss)# 每100次迭代打印进度if i % 100 == 0:print(f"迭代 {i}: 损失 = {loss:.6f}")return theta, loss_history# 使用模型进行预测
def predict(X, theta, degree=2):"""使用训练好的模型进行预测"""X_poly = create_polynomial_features(X, degree)return X_poly.dot(theta)# 计算模型性能指标
def evaluate_model(y_true, y_pred):"""计算模型性能指标"""mse = np.mean((y_true - y_pred) ** 2)rmse = np.sqrt(mse)mae = np.mean(np.abs(y_true - y_pred))# 计算R²ss_res = np.sum((y_true - y_pred) ** 2)ss_tot = np.sum((y_true - np.mean(y_true)) ** 2)r2 = 1 - (ss_res / ss_tot)return {"MSE": mse,"RMSE": rmse,"MAE": mae,"R²": r2}# 可视化结果
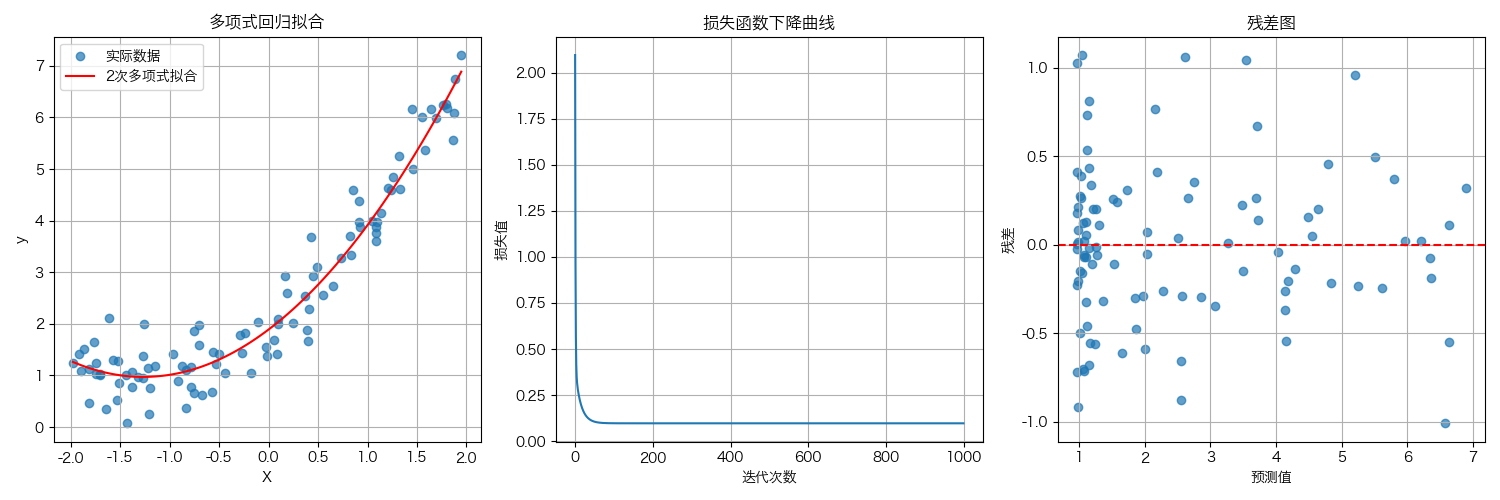
def plot_results(X, y, y_pred, loss_history, degree):"""可视化数据和模型拟合结果"""plt.figure(figsize=(15, 5))# 绘制数据和拟合曲线plt.subplot(1, 3, 1)plt.scatter(X, y, alpha=0.7, label='实际数据')# 创建平滑曲线用于绘制拟合结果X_test = np.linspace(X.min(), X.max(), 100).reshape(-1, 1)y_test = predict(X_test, theta_opt, degree)plt.plot(X_test, y_test, 'r-', label=f'{degree}次多项式拟合')plt.xlabel('X')plt.ylabel('y')plt.title('多项式回归拟合')plt.legend()plt.grid(True)# 绘制损失下降曲线plt.subplot(1, 3, 2)plt.plot(loss_history)plt.xlabel('迭代次数')plt.ylabel('损失值')plt.title('损失函数下降曲线')plt.grid(True)# 绘制残差图plt.subplot(1, 3, 3)residuals = y - y_predplt.scatter(y_pred, residuals, alpha=0.7)plt.axhline(y=0, color='r', linestyle='--')plt.xlabel('预测值')plt.ylabel('残差')plt.title('残差图')plt.grid(True)plt.tight_layout()plt.show()# 运行主函数
if __name__ == "__main__":# 设置多项式次数degree = 2# 生成数据X, y = generate_sample_data(n_samples=100, noise=0.5, degree=degree)# 创建多项式特征X_poly = create_polynomial_features(X, degree)# 初始化参数theta_init = np.random.randn(X_poly.shape[1], 1)# 设置超参数alpha = 0.1  # 学习率lambda_ = 0.01  # 正则化强度iterations = 1000print(f"初始参数: {theta_init.ravel()}")print(f"初始损失: {compute_loss(X_poly, y, theta_init, lambda_):.6f}")print("\n开始训练...")# 训练模型theta_opt, loss_history = gradient_descent(X_poly, y, theta_init, alpha, lambda_, iterations)print("\n训练完成!")print(f"优化后的参数: {theta_opt.ravel()}")print(f"最终损失: {compute_loss(X_poly, y, theta_opt, lambda_):.6f}")# 进行预测y_pred = predict(X, theta_opt, degree)# 评估模型metrics = evaluate_model(y, y_pred)print("\n模型性能:")for metric, value in metrics.items():print(f"{metric}: {value:.4f}")# 可视化结果plot_results(X, y, y_pred, loss_history, degree)# 打印多项式方程equation = "y = "for i, coef in enumerate(theta_opt.ravel()):if i == 0:equation += f"{coef:.4f}"else:sign = "+" if coef >= 0 else ""equation += f" {sign} {coef:.4f}x"if i > 1:equation += f"^{i}"print(f"\n拟合的多项式方程: {equation}")

代码说明

这个多项式回归模型包含以下主要组件：

数据生成：generate_sample_data() 函数生成二次多项式数据
特征工程：create_polynomial_features() 函数将原始特征转换为多项式特征
损失计算：compute_loss() 函数计算带有L2正则化的均方误差
梯度计算：compute_gradient() 函数计算梯度，包括L2正则化项
优化算法：gradient_descent() 函数执行梯度下降优化
预测函数：predict() 函数使用训练好的模型进行预测
评估函数：evaluate_model() 函数计算各种性能指标
可视化：plot_results() 函数可视化数据、拟合曲线、损失下降和残差

多项式回归特点

特征转换：通过创建多项式特征，将非线性问题转化为线性问题
模型灵活性：可以拟合各种复杂的非线性关系
过拟合风险：高阶多项式容易过拟合，需要使用正则化
正则化：L2正则化帮助控制模型复杂度，防止过拟合

超参数设置

● degree=2：多项式次数（可以调整以拟合更复杂的曲线）
● alpha=0.1：学习率
● lambda_=0.01：正则化强度
● iterations=1000：迭代次数

运行结果

运行此代码将输出：

初始和优化后的参数
训练过程中的损失变化
模型在测试数据上的性能指标
数据点、拟合曲线、损失下降曲线和残差图的可视化
拟合的多项式方程

初始参数: [ 0.01300189  1.45353408 -0.26465683]
初始损失: 5.284633开始训练...
迭代 0: 损失 = 2.094630
迭代 100: 损失 = 0.097529
迭代 200: 损失 = 0.097271
迭代 300: 损失 = 0.097271
迭代 400: 损失 = 0.097271
迭代 500: 损失 = 0.097271
迭代 600: 损失 = 0.097271
迭代 700: 损失 = 0.097271
迭代 800: 损失 = 0.097271
迭代 900: 损失 = 0.097271训练完成!
优化后的参数: [1.8907338  1.4501427  0.57258078]
最终损失: 0.097271模型性能:
MSE: 0.1943
RMSE: 0.4408
MAE: 0.3389
R²: 0.9421

在这里插入图片描述

其它知识

如何解读您的多项式回归模型的残差图

上述测试代码中引入了残差图，那么如何利用残差图来衡量评价算法模型的好与坏呢？把握以下几个原则即可

检查随机性：残差是否随机分布在零线上下？如果是，表明模型基本捕捉了数据中的模式。
检查方差恒定性：残差的变异性是否在整个预测值范围内大致相同？如果出现喇叭形或锥形，可能需要调整模型。
识别异常值：是否有明显远离其他点的残差？这些点可能是异常值或杠杆点。
检查模式：是否有任何曲线模式或趋势？如果有，表明模型可能没有充分捕捉数据中的非线性关系。

为什么使用平方误差（MSE）而不是绝对值或更高次方

在回归问题中，我们使用平方误差（MSE）而不是绝对值误差（MAE）或更高次方误差，这背后有深刻的数学和统计原理。
对大误差给予更高惩罚，平方运算确实会放大较大误差，但这正是我们想要的：

# 不同误差大小的惩罚对比
errors = [0.1, 0.5, 1.0, 2.0, 5.0]print("误差值 | 绝对值惩罚 | 平方惩罚 | 三次方惩罚")
print("-" * 45)
for error in errors:abs_penalty = abs(error)square_penalty = error**2cubic_penalty = abs(error)**3print(f"{error:5.1f} | {abs_penalty:11.2f} | {square_penalty:9.2f} | {cubic_penalty:10.2f}")

输出结果会显示：
● 小误差（0.1）：平方惩罚（0.01）比绝对值惩罚（0.1）更轻
● 大误差（5.0）：平方惩罚（25.0）比绝对值惩罚（5.0）重得多
这种特性使得模型更加关注减少大的误差，这通常是我们想要的。因为它使模型更加关注减少较大的预测错误。在实际应用中，可以根据具体问题选择合适的损失函数，但MSE因其良好的数学性质和统计基础而成为最常用的选择。

查看全文

http://www.dtcms.com/a/362149.html