当前位置：首页 > news >正文

【笔记】float类型的精度有限，无法精确表示123456.6789

news 2025/9/2 11:39:22

一、前情提要

有个Java数据转换的小示例：

public class Example2_2 {public static void main(String[] args) {float f = 123456.6789f;System.out.printf("f=%30.12f", f);}
}

输出的结果是：
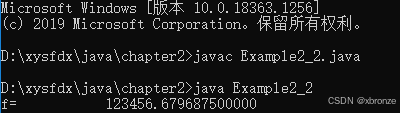
在这里插入图片描述

123456.679687500000

这里就发现了个问题，我变量f定义的值是123456.6789，为什么输出的结果小数位变了呢？？

简单来说,核心原因是 float类型的精度有限，无法精确表示123456.6789

Java 中float是32 位单精度浮点数，遵循 IEEE 754 标准。它的存储结构由 1 位符号位、8 位指数位和 23 位尾数位（实际有效精度约 24 位）组成。
这种结构导致float只能精确表示有限的十进制小数，对于大多数十进制小数（如代码中的123456.6789），它无法精确存储，只能存储一个最接近的近似值。

那么如何理解float类型无法精确表示123456.6789？？

要理解“float类型无法精确表示123456.6789”，需要从计算机如何存储小数说起。这本质上是“二进制与十进制的转换限制”和“float的存储空间有限”共同导致的问题，我们一步步拆解：

二、计算机如何存储小数以及float空间限制

1. 计算机只认识二进制，不认识十进制

我们日常用的是十进制（0-9），但计算机内部所有数据（包括小数）都必须转换成二进制（0和1）存储。
对于整数（如123），十进制转二进制是“除2取余”，结果是有限的二进制数（比如123的二进制是1111011），可以精确存储。

但小数的转换要复杂得多：十进制小数转二进制的方法是“乘2取整”，例如0.6789转二进制的过程是：

0.6789 × 2 = 1.3578 → 取整数部分1（二进制小数第一位是1）
剩下的0.3578 × 2 = 0.7156 → 取整数部分0（第二位是0）
剩下的0.7156 × 2 = 1.4312 → 取整数部分1（第三位是1）
剩下的0.4312 × 2 = 0.8624 → 取整数部分0（第四位是0）
… 以此类推

这个过程可能无限进行下去（永远无法得到整数1.0），就像十进制中1/3=0.3333…无限循环一样。
也就是说：大部分十进制小数无法用有限长度的二进制精确表示，只能得到一个近似值。

2. float类型的“存储空间”被严格限制

Java的float是32位单精度浮点数，遵循IEEE 754标准，它的存储空间被分成3部分：

1位符号位（表示正负）
8位指数位（表示数值的大小范围）
23位尾数位（表示数值的精度，即有效数字）

关键限制在这里：尾数位只有23位（加上默认的1位隐藏位，总共24位有效精度）。
24位二进制能表示的有效数字相当于多少位十进制呢？
通过公式换算：24 × log₁₀(2) ≈ 7.2位。
也就是说：float最多只能精确表示6-7位十进制有效数字，超过这个范围的数字会被“舍入”，导致精度丢失。