一文通透!为什么 DBSCAN 能检测任意形状的簇 ?
哈喽,我是我不是小 upper!~
今儿咱们知识星球中有同学提了个特别关键的问题:“为什么 DBSCAN 能检测任意形状的簇?” 其实在机器学习聚类的学习里,搞懂这种 “原理细节”,远比死记算法步骤重要 —— 它能帮你真正明白模型 “能做什么”“为什么能做”,遇到实际问题时也不会乱用模型。
接下来我就用最通俗的话,从 DBSCAN 的基础原理讲起,一步步拆解到核心问题,咱们把 “任意形状聚类” 这件事彻底说透。
先搞懂:DBSCAN 到底是个啥?
先给 DBSCAN 一个 “身份卡”:它的全称是 Density-Based Spatial Clustering of Applications with Noise,翻译过来就是 “基于密度的噪声应用空间聚类算法”。光看名字就能抓重点 —— 它是靠 “密度” 来判断簇的,还能顺便把 “噪声点”(异常值)挑出来。
咱们先用一句话总结它的核心逻辑: DBSCAN 会把点云中 “挨得近、密度高” 的点归成一类,同时把那些 “孤零零、周围没几个点” 的点标记成噪声,既不用提前说要分几类,也不强行给所有点归类。
对比咱们最熟悉的 K-Means,DBSCAN 的两个 “过人之处” 一下子就凸显出来了:
- 不用预设簇数量 k:K-Means 必须先告诉它 “要分 3 类还是 5 类”,但 DBSCAN 能自己从数据密度里 “摸出” 簇的数量;
- 能抓任意形状的簇:K-Means 像个 “圆规”,只能找到围绕中心点的 “球状簇”,但 DBSCAN 能抓月牙形、环形、蛇形这些 “不规则形状” 的簇。
也正因为这两个特点,DBSCAN 在很多实际场景里特别好用 —— 比如地理数据里找 “商业区聚集区”“居民区斑块”,图像分析里分割不规则的目标区域,甚至工业检测里找 “异常设备信号点”,都能派上用场。
拆解 DBSCAN 的核心原理:3 个关键概念 + 1 套聚类逻辑
要搞懂 “任意形状” 的秘密,得先吃透 DBSCAN 的 “底层语言”—— 它靠几个核心概念定义 “簇”,再用一套逻辑把簇 “拼” 出来。咱们一个个说,都用 “大白话 + 数学定义” 双管齐下,保证好懂。
1. 第一个基础:ε- 邻域(ε-neighborhood)—— 给点画个 “朋友圈”
你可以把每个数据点想象成一个人,ε(读作 “伊普西隆”)就是这个人 “交朋友的距离标准”:只要另一个人在 “以自己为中心、半径为 ε 的圆(二维)/ 球体(高维)” 里,就算进了自己的 “朋友圈”。
数学定义: 对于任意数据点 (X 是整个数据集),其 ε- 邻域记为
,定义为:
这里的
是点
和
之间的距离,常用的有欧氏距离(适合低维数据)、曼哈顿距离(适合高维或稀疏数据)等,具体选哪种根据数据场景定,但核心都是 “衡量两点有多近”。
举个例子:如果 ε=2,点 的坐标是 (0,0),那么所有满足
的点
,都在
的 ε- 邻域里 —— 就像以 (0,0) 为中心画个半径 2 的圆,圆内所有点都是
的 “邻居”。
2. 三个核心点类型:核心点、边界点、噪声点 —— 给点 “贴标签”
有了 “朋友圈”(ε- 邻域),DBSCAN 会根据 “朋友圈里的人数”,给每个点贴三个标签之一。这里要引入第二个参数 MinPts(Minimum Points,最小点数)—— 可以理解为 “构成一个‘热闹区域’至少需要的人数”。
咱们一个个说清楚:
(1)核心点(Core Point)——“朋友圈够热闹,自己是核心”
如果一个点的 ε- 邻域里,至少有 MinPts 个点(包含它自己),那它就是核心点。换句话说,这个点周围 “人够多”,能撑起一个 “热闹的小区域”,是构成簇的 “骨架”。
数学定义: 若 ,则
为核心点。 这里的
表示 ε- 邻域里点的数量(集合的基数)。
比如设 MinPts=5:如果点 的 ε- 邻域里有 6 个点(包括自己),那它就是核心点 —— 这说明它周围 “够密”,能作为簇的 “起点”。
(2)边界点(Border Point)——“自己朋友圈不热闹,但在别人的热闹圈里”
如果一个点的 ε- 邻域里,点数少于 MinPts,但它 “刚好在某个核心点的 ε- 邻域里”,那它就是边界点。简单说:这个点自己周围不热闹,但 “蹭到了核心点的热闹”,属于簇的 “边缘部分”,会被归到核心点所在的簇里。
数学定义: 若 ,且存在核心点
使得
,则
为边界点。
举个例子:MinPts=5,点 的 ε- 邻域里只有 3 个点(不够 MinPts),但它刚好在核心点
的 ε- 邻域里 —— 那
就是边界点,会被归到
所在的簇里,相当于 “簇的边缘点”。
(3)噪声点(Noise Point / Outlier)——“自己不热闹,也蹭不到别人的热闹”
既不是核心点、也不是边界点的点,就是噪声点。这些点 “孤零零” 的,周围既没有足够多的邻居,也不在任何核心点的邻域里,会被 DBSCAN 标记为 “异常值”,不归属任何簇。
数学定义: 若 ,且不存在任何核心点
使得
,则
为噪声点。
比如:点 的 ε- 邻域里只有 2 个点(MinPts=5),且没有任何核心点的邻域能覆盖它 —— 那它就是噪声点,比如数据里的测量误差、异常样本等。
3. 点与点的 “关系网”:密度可达、密度相连 —— 把点 “串成簇”
有了 “点的标签”,DBSCAN 还需要一套 “规则”,判断不同点之间能不能 “归为一类”。这就需要两个关键关系:密度可达和密度相连—— 正是这两个关系,为 “任意形状簇” 埋下了伏笔。
(1)直接密度可达(Directly Density-Reachable)——“一步到位的邻居”
如果点 在点
的 ε- 邻域里,而且
是核心点,那我们就说 “
从
直接密度可达”。简单说:核心点
的 “朋友圈” 里的点
,和
是 “直接邻居”,能直接归为一类。
数学定义: 若 且
为核心点,则
从
直接密度可达,记为
。
这里要注意:直接密度可达是 “单向” 的 —— 只有核心点能 “带动” 别人,边界点不行。比如 是核心点,
在它的邻域里,那
从
直接可达;但如果
是边界点,就算
在
的邻域里,也不能说
从
直接可达(因为
不是核心点,没资格 “带动” 别人)。
(2)密度可达(Density-Reachable)——“多步串联的邻居”
如果存在一串点 ,每一步都是 “直接密度可达”,那我们就说 “
从
密度可达”。简单说:通过核心点 “一步步传递”,能把
和
串起来,就算同一类。
数学定义: 若存在点序列 ,使得
,
,…,
,则
从
密度可达。
举个例子:假设 是核心点,
在
的邻域里(直接可达);
也是核心点,
在它的邻域里(直接可达);
还是核心点,
在它的邻域里 —— 那
就从
密度可达,它们会被归为同一个簇。
(3)密度相连(Density-Connected)——“有共同核心朋友的邻居”
如果存在一个 “中间点 ”,使得
和
都从
密度可达,那我们就说 “
和
密度相连”。简单说:两个点虽然不能直接串起来,但它们有同一个 “核心点朋友”,那也能归为一类。
数学定义: 若存在点 ,使得
从
密度可达且
从
密度可达,则
和
密度相连。
比如: 从核心点
密度可达,
也从
密度可达 —— 哪怕
和
之间隔得远,没有直接的 “密度路径”,它们也会因为 “共同的核心朋友
” 被归为同一簇。
4. DBSCAN 聚类的完整步骤:像 “寻宝” 一样找簇
搞懂了上面的概念,DBSCAN 的聚类过程就像 “在点云中寻宝”—— 找到核心点,再顺着核心点的 “关系网” 把整个簇挖出来。咱们用大白话拆解成 5 步:
- 初始化:给所有数据点贴上 “未处理” 标签,簇的计数器设为 0(还没找到任何簇);
- 遍历未处理的点:随便选一个 “未处理” 的点
,把它标记为 “已处理”;
- 判断是否为核心点:计算
的 ε- 邻域
,看里面的点数是否 ≥ MinPts:
- 如果 不够 MinPts:把
暂时标记为 “噪声点”(后面如果发现它在某个核心点的邻域里,会重新归为边界点);
- 如果 够 MinPts:簇计数器 +1(新簇诞生),把
加入这个新簇,同时把
里的所有点放进一个 “待扩展队列”(这些点可能都是簇的一部分);
- 如果 不够 MinPts:把
- 扩展簇:顺着 “关系网” 找所有相关点:
- 从 “待扩展队列” 里取出一个点
,如果
是 “未处理” 的,先标记为 “已处理”;
- 计算
的 ε- 邻域,如果
是核心点(邻域点数 ≥ MinPts),就把它邻域里的所有点加入 “待扩展队列”;
- 如果
还没被归到任何簇里,就把它加入当前簇;
- 重复这个过程,直到 “待扩展队列” 为空(当前簇的所有点都找到了);
- 从 “待扩展队列” 里取出一个点
- 重复直到所有点处理完:回到步骤 2,继续选下一个 “未处理” 的点,直到所有点都被标记为 “已处理”(要么归为某个簇,要么是噪声点)。
整个过程就像:你在森林里(点云)找宝藏(簇),找到一个 “核心点”(宝藏的入口),然后顺着入口的通道(密度可达关系),把所有连通的通道(相关核心点、边界点)都探索完,整个通道网络就是一个簇 —— 至于通道是直的、弯的还是绕圈的,根本不影响,只要连通就能全找到。
核心问题:为什么 DBSCAN 能检测任意形状的簇?
终于到了最关键的部分!咱们先反过来想:为什么 K-Means 只能找 “球状簇”?因为 K-Means 的核心逻辑是 “最小化簇内点到簇中心的距离和”—— 它默认簇是 “围绕一个中心点的球形区域”,一旦簇的形状是弯的、环的,中心点就会 “跑偏”,导致聚类失败(比如环形簇会被 K-Means 分成两个半圆)。
而 DBSCAN 之所以能突破 “形状限制”,核心原因就一个:它用 “密度连通性” 定义簇,而不是 “中心点距离”。咱们从 “直观理解” 和 “数学逻辑” 两个层面说透。
1. 直观理解:像 “走迷宫” 一样,连通的密度区域就是一个簇
想象你面前有两堆点:一堆是 “环形”(像甜甜圈),另一堆是 “弯月形”(像月牙),每堆点的密度都足够高(邻域能连起来)。
用 DBSCAN 处理时,它的逻辑是这样的:
- 对于 “环形簇”:随便找一个环上的核心点
,它的 ε- 邻域里有足够多的点(≥ MinPts),进入 “扩展阶段”;顺着
的邻域找到下一个核心点
,再顺着
的邻域找下一个…… 直到绕环一圈,把整个环上的核心点、边界点都串起来 —— 哪怕环的中心是空的,只要环上的点 “密度连通”,就会被归为一个簇;
- 对于 “弯月形簇”:从月牙 “尖端” 的核心点出发,顺着月牙的弧度,一步步扩展邻域 —— 月牙再弯,只要每一段的点都够密(核心点能连起来),就能把整个月牙都 “走” 出来,不会因为形状弯曲而把它分成多段。
这就像走迷宫:只要通道是连通的(密度够),不管迷宫是直的、弯的还是绕圈的,你都能从入口走到出口,把整个迷宫逛完 ——DBSCAN 找簇的逻辑也是如此,不管簇的形状多不规则,只要点的 “密度路径” 是连通的,就能把整个簇找出来。
2. 数学逻辑:密度可达与密度相连,打破 “形状依赖”
从数学上看,DBSCAN 能处理任意形状簇的关键,就藏在 “密度可达” 和 “密度相连” 的定义里 —— 这两个关系不依赖任何 “形状假设”,只依赖 “点的连通性”。
咱们再回顾两个核心定义,就能明白其中的逻辑:
比如有一个 “蛇形簇”,点的分布是 (像蛇一样弯曲延伸),且每个相邻点都满足 “核心点 +ε- 邻域覆盖” 的条件:
是核心点,
在
的 ε- 邻域里(
从
直接密度可达);
也是核心点,
在
的 ε- 邻域里(
从
直接密度可达);以此类推,直到
是核心点,
在
的 ε- 邻域里(
从
直接密度可达)。根据密度可达的定义,
从
) 密度可达,所以整个 “蛇形链” 上的点都会被归为同一个簇 —— 哪怕蛇身弯了 3 个弯、绕了 2 个圈,只要每一段 “相邻核心点” 的 ε- 邻域能连起来,整个蛇形区域就会被完整识别。这里的关键是:密度可达不要求 “全局距离近”,只要求 “局部邻域连通”。K-Means 会因为 “蛇头和蛇尾的直线距离远” 而把它们分成两个簇,但 DBSCAN 只看 “蛇身上的点能不能通过局部邻域一步步串起来”—— 只要能串起来,再长、再弯的形状也能算一个簇。
2)密度相连:解决 “间接连通” 的簇结构
还有一种更复杂的情况:簇不是 “一条链”,而是 “多个分支”,比如像 “Y 字形” 的簇 —— 是中心核心点,
、
、
分别是三个分支的核心点,且每个分支又延伸出一串点。
此时:
- 分支 1 的点
从
密度可达,
从
密度可达,所以
从
密度可达;
- 分支 2 的点
从
密度可达,
从
密度可达,所以
从
密度可达;
- 分支 3 的点
从
密度可达,
从
密度可达,所以
从
密度可达。
根据密度相连的定义,、
、
因为 “共同的核心点
” 而密度相连,最终会被归为同一个 “Y 字形簇”。
这种情况下,K-Means 会因为三个分支的 “中心点距离远” 而分成三个簇,但 DBSCAN 能通过 “中心核心点 + 密度相连” 的逻辑,识别出这是一个 “多分支连通” 的整体 —— 这也是 “任意形状” 能力的重要补充。
3. 对比 K-Means:用 “局部密度” 替代 “全局中心”,打破形状限制
为了更直观,咱们用一个具体例子对比两种算法的差异:假设数据是 “环形簇”(比如半径 5-6 的圆环,中心是空的),MinPts=5,ε=0.8(邻域能覆盖圆环上相邻的点)。
- K-Means 的表现:它会计算所有点的 “均值中心”,而环形的均值中心在圆环内部(空区域)。K-Means 会把圆环上的点分成 “离均值中心近的两半”—— 比如上半圆和下半圆,最终得到两个错误的 “半圆簇”,完全丢失了 “环形” 的真实结构;
- DBSCAN 的表现:
- 选圆环上一个点
,计算其 ε- 邻域 —— 因为圆环上的点密度足够,邻域里有 ≥5 个点,
成为核心点,启动新簇;
- 扩展簇时,把
邻域里的点加入队列,这些点也是核心点(邻域点数够),再把它们的邻域点加入队列;
- 顺着圆环一步步扩展,直到绕圆环一圈,所有圆环上的点都被归为同一个簇,中心的空区域和外部的孤立点被标记为噪声 —— 完美还原了 “环形” 的真实形状。
- 选圆环上一个点
这个例子能清晰看到:K-Means 的 “全局中心 + 距离” 逻辑,本质上是 “用球形边界拟合簇”,所以只能处理凸形、球形结构;而 DBSCAN 的 “局部密度 + 连通性” 逻辑,是 “用密度连通区域定义簇”,不管簇是凸的、凹的、弯的、环的,只要局部密度能连起来,就能准确识别。
关键补充:ε 和 MinPts 的选择,影响 “任意形状” 的识别效果
虽然 DBSCAN 能处理任意形状,但它的效果依赖两个参数的选择:ε(邻域半径)和 MinPts(最小核心点数)—— 这两个参数直接决定了 “哪些点算核心点”“哪些点能连通”。
举个例子:
- 如果 ε 选得太小:邻域覆盖不到相邻的点,原本连通的簇会被拆成多个 “小碎片簇”(比如蛇形簇被拆成多段);
- 如果 ε 选得太大:邻域会覆盖不同簇的点,导致原本独立的簇被合并成一个 “大杂烩簇”(比如两个相邻的环形簇被连成一个);
- 如果 MinPts 选得太大:很多原本是核心点的点会变成边界点,簇的扩展会 “断链”(比如蛇形簇中间的点不够 MinPts,导致蛇头和蛇尾分成两个簇);
- 如果 MinPts 选得太小:容易把噪声点误判为核心点,形成 “虚假的小簇”(比如孤立的噪声点因为邻域里有 2 个点,被误判为核心点,形成一个 “假簇”)。
所以,实际使用 DBSCAN 时,需要通过 “肘部法则”(比如绘制 k - 距离图,找邻域点数突变的 ε)或领域经验调整参数 —— 但无论如何,参数的影响是 “能否准确识别连通性”,而不是 “能否识别任意形状” 本身。只要参数合适,DBSCAN 对形状的适应性不会改变。
总结:DBSCAN 识别任意形状簇的本质
一句话概括:DBSCAN 把簇定义为 “密度连通的点集”,而非 “围绕中心的球形区域”。
它通过 “ε- 邻域” 定义局部密度,用 “核心点” 作为簇的骨架,靠 “密度可达” 和 “密度相连” 构建点与点的连通关系 —— 这种逻辑不依赖任何预设的形状假设,只要数据点的局部密度能形成 “连通路径”,无论路径是直的、弯的、环形的还是多分支的,都能被完整识别为一个簇。
这也是为什么在处理地理数据、图像分割、异常检测等 “非球形簇” 场景时,DBSCAN 会成为比 K-Means 更实用的选择 —— 它真正做到了 “让数据自己定义簇的形状”。
代码体现
下面我们用 Python 写一个例子,用两个经典的“月牙形”数据来验证。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN, KMeans# 生成数据:两个弯月形
X, y = make_moons(n_samples=1000, noise=0.05, random_state=42)# K-Means 聚类
kmeans = KMeans(n_clusters=2, random_state=42)
y_kmeans = kmeans.fit_predict(X)# DBSCAN 聚类
dbscan = DBSCAN(eps=0.2, min_samples=5)
y_dbscan = dbscan.fit_predict(X)# 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 5))# K-Means
axes[0].scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='viridis')
axes[0].set_title("K-Means 聚类结果")# DBSCAN
axes[1].scatter(X[:, 0], X[:, 1], c=y_dbscan, cmap='viridis')
axes[1].set_title("DBSCAN 聚类结果")plt.show()K-Means:会把月牙形硬生生切成两半(中间有条直线分割)。
DBSCAN:能完整识别两个弯月形簇,没有被分裂。
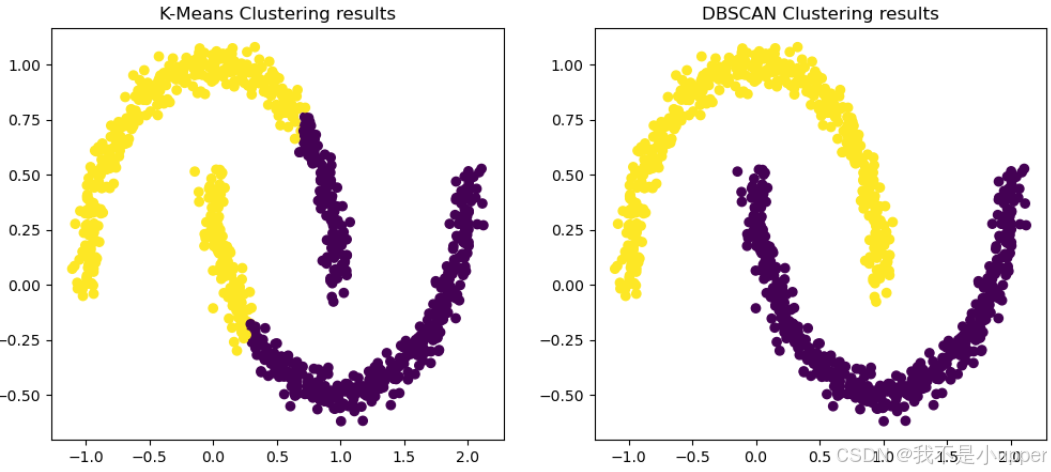
这就是 DBSCAN“任意形状检测”的直观演示,大家也很容易理解~
整体上,大家可以看到DBSCAN 基于 密度 来定义簇,不依赖簇中心。密度可达、密度相连 的定义,让它能够扩展出任意形状的簇。
数学公式说明:只要存在一条“密度路径”,两个点就属于同一个簇。
最后实验表明:DBSCAN 能识别月牙形、环形等 K-Means 无法处理的复杂簇。
在这个问题之后呢,其实还剩余其他的一些问题,比如:
对比 DBSCAN 和其他聚类方法(K-Means、层次聚类、MeanShift 等);
更深入的公式推导,比如 ε-邻域的度量方式、高维空间问题;
参数选择(eps、MinPts 如何选);
DBSCAN 的缺点和改进版本(HDBSCAN、OPTICS);
.....
