对于牛客网—语言学习篇—编程初学者入门训练—复合类型：BC136 KiKi判断上三角矩阵及BC139 矩阵交换题目的解析
开篇介绍：
hello 大家，上篇博客我们分析完了牛客网—语言学习篇—编程初学者入门训练—复合类型：二维数组中较为简单的题目，在末尾，我提到了会对这一部分题目中较为困难的题目进行单独分析，于是，今天它们便来了，在这里说明一下：虽然这部分题目中较难的题目有7道，但是由于题目难度较大，一篇就讲完的话，大家可能会囫囵吞枣，精力也无法完全一次性吃透，所以我变打算将这7道题目拆分成3篇文章来进行讲解，选取思路较为类似的几道题目为一篇博客，帮助大家更加理解题目并提高应对能力。
那么本篇文章选取的便是BC136 KiKi判断上三角矩阵、BC139 矩阵交换这两道题目来进行讲解，它们在牛客网中的评定为中等，难度也算是还行，但是我这边可以直接和大家说，其实这两题并不难，所以希望大家不要有畏缩心理，要敢于挑战，相信大家肯定能够吃透这两题。
下面附上这两题链接，老规矩，大家可以在看讲解之前便练练手，加深对题目的印象以及理解。
KiKi判断上三角矩阵_牛客题霸_牛客网
https://www.nowcoder.com/practice/9a6786c28cdb45f9b991685f867b5d08?tpId=290&tqId=828864&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290矩阵交换_牛客题霸_牛客网https://www.nowcoder.com/practice/ec44d4ff8c794b2f9205bdddbde96817?tpId=290&tqId=618637&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E8%25AF%25AD%25E8%25A8%2580%25E5%25AD%25A6%25E4%25B9%25A0%25E7%25AF%2587%26topicId%3D290下面我们便开始逐题分析。
在这里我先申明一下，接下来本文所讲的方法，对于二维数组元素的输入，都是采用忽略0行0列，从1行1列开始输入，大家有不懂的可以看一下这篇博客：
对于牛客网—语言学习篇—编程初学者入门训练—复合类型：二维数组较简单题目的解析-CSDN博客
BC136 KiKi判断上三角矩阵：
这道题的难度可以说是有名无实，只要我们细心观察，便会发现，这题只是一个纸老虎，我们先看题目：
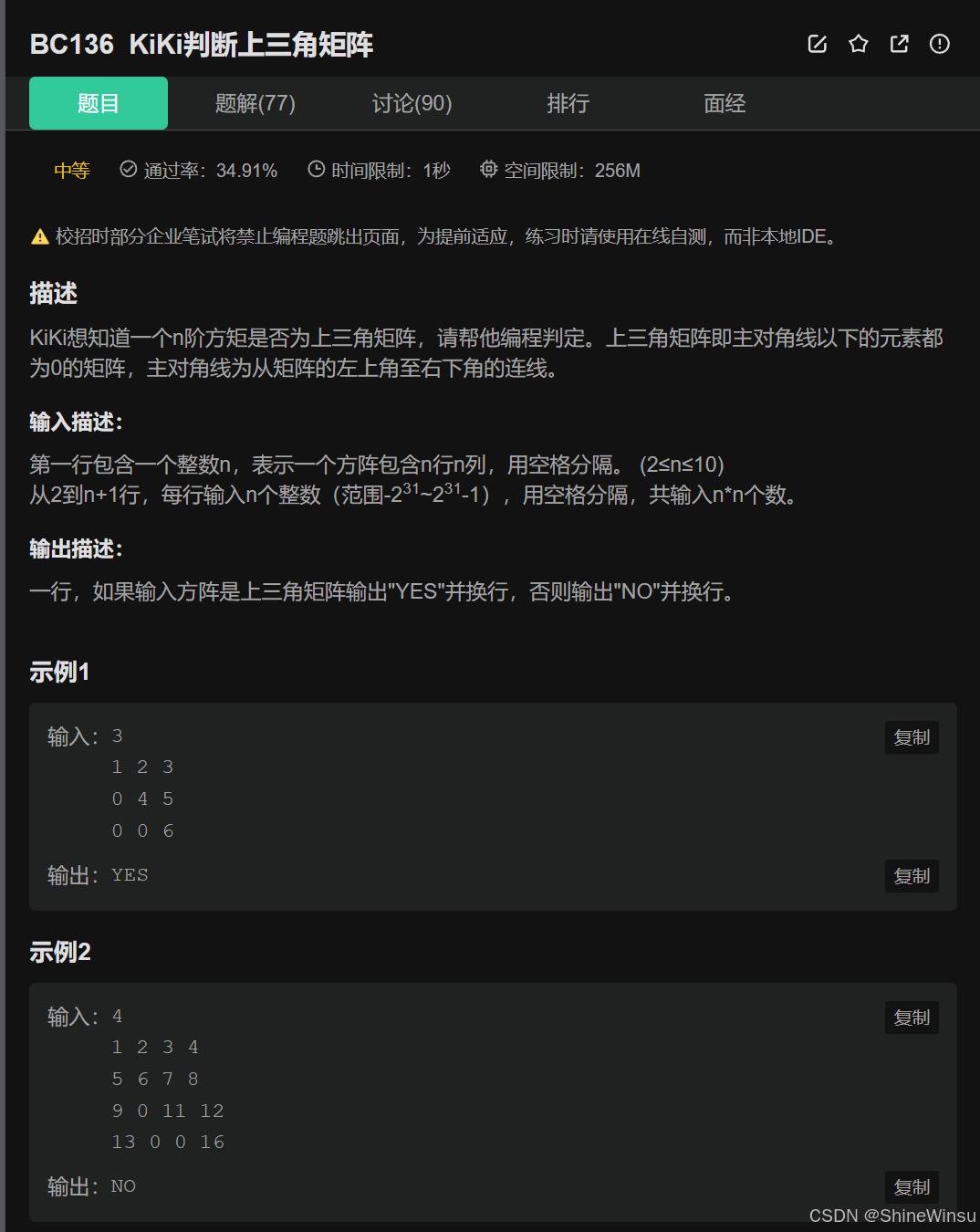
题意分析：
这道题的核心是判断一个 n 阶方阵是否为上三角矩阵。上三角矩阵的定义是主对角线以下的元素都为 0（主对角线是从矩阵左上角到右下角的连线）。
输入部分
- 首先输入一个整数 n（2≤n≤10），表示方阵的行数和列数。
- 接着输入 n 行，每行 n 个整数，构成这个 n×n 的方阵。
处理逻辑
需要遍历矩阵中主对角线下方的所有元素（即行号大于列号的位置，也就是 i>j，其中 i 是行索引，j 是列索引），检查这些位置的元素是否都为 0。如果有任何一个这样的元素不为 0，则该矩阵不是上三角矩阵；只有当所有主对角线下方的元素都为 0 时，才是上三角矩阵。
输出部分
根据判断结果，输出 “YES”（是上三角矩阵）或者 “NO”（不是上三角矩阵）。
继续解答：
知道了题意之后，我们便可以开始着手于分析解题所需步骤，对于这道题，我这边给大家分享两种解法：
方法一：
这边我想要强调一下，大家在面对二维数组的题目时，如果不能一眼就有思路的话，希望大家不要去干瞪眼，大家可以将二维数组中每一个元素的坐标都表示出来，去看看是否有什么规律，说不定解题的关键点便是蕴含在其中。
这道题便是如此，我们第一眼估计很难有什么思路，只知道要去判断上三角矩阵，然后这个矩阵的位置是在对角线下面的，但是我们要怎么去找这个上三角矩阵的所有元素呢？这一点是一个难点，需要我们的解决，那么，我们不妨把例子中的上三角矩阵的所有元素的坐标都标出来一下：
| 元素值 | 坐标 |
|---|---|
| 0 | (2,1) |
| 0 | (3,1) |
| 0 | (3,2) |
嘶，光看这些，感觉还是，没有什么思路，那要不我们稍微扩大一些范围，既然题目有提到主对角线，那我们不妨将主对角线的元素坐标进行分析一下，注意，主对角线的元素的坐标中的行和列都是相同的，
| 元素值 | 坐标 |
|---|---|
| 1 | (1,1) |
| 4 | (2,2) |
| 6 | (3,3) |
其实如果大家洞察力超强的话，已经能看出端倪来了，不过要是大家没看出来，也没事，可能是因为我把这些元素都拆分成表格的形式，比较分散，这边建议大家标元素坐标的话，可以直接标在每个元素下面，就像这样子：
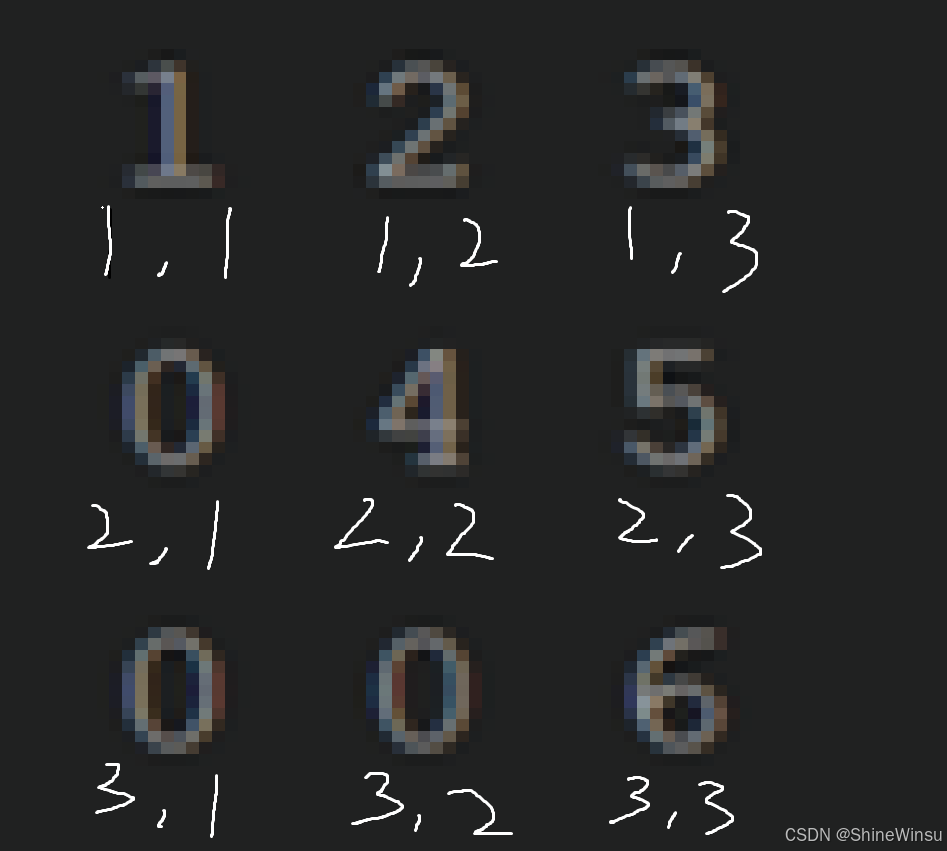
这么标注之后，大家应该就能清晰很多，接下来便让我们详细观察一下上三角矩阵的元素坐标以及主对角线元素的坐标，首先大家应该很清楚，本题的关键点便是上三角矩阵和主对角线，所以我们解答本题的关键也在于要找出上三角矩阵和主对角线的关系。
由于第一个元素1，它虽然也算是上三角矩阵，但是由于它也在主对角线上，所以我们不考虑它，我们从下面的0开始分析，元素4是主对角线在第二行的元素，坐标为（2，2），而第二行中的0，便算是上三角矩阵在第二行的元素，坐标为（2，1），大家对比这两个坐标，有没有发现什么，不错，它们两个的行坐标是相同的，而列坐标却是0的小于4，这是特例吗？
我们再看一下第三行的上三角矩阵和主对角线的元素坐标对比，即如上图，wow！！！，好像也是诶，是的，恭喜你，你找到了上三角矩阵和主对角线元素坐标的关系，那便是：在某一行中，二者行坐标相同，而列坐标一定是上三角矩阵元素的列坐标小于主对角线元素的列坐标。
发现了这一点之后，距离解决这道题就近在咫尺了，我们已经知道了二者的联系，但是我们要怎么用代码实现呢？首先，我们需要知道，我们需要对上三角矩阵的所有元素都进行遍历，只要有一个不为0，那就代表要表达出“NO”，而这便需要我们判断素数时的相同手段，设置一个标识变量flag，详见这篇博客：对于判断素数（质数）以及牛客网—语言学习篇—编程初学者入门训练—复合类型：字符/字符数组的题目解析-CSDN博客
这是关键一步，接下来我们便需要去找到上三角矩阵的所有元素了，经过上面的分析，我们知道了二者关系，那么我们便可以利用这个关系去进行遍历上三角矩阵的所有元素，首先最外层循环，也就是行i的循环，还是正常的，要从第一行遍历到最后一行，只是对于内部循环，即列j的循环，就不能跟平时遍历二维数组所有元素时的一样了，毕竟我们只遍历在主对角线之下的上三角矩阵的所有元素，行自然是没问题，列我们就得改了，那么要怎么改呢？
首先列j自然还是要从第一列开始进行遍历（毕竟第二行的上三角矩阵元素是在第一列），那么这也就说明，我们要对j的限制条件进行更改了，那么要从原本for (int j = 1; j <= n; j++)（这个是遍历到最后一列）改为什么呢？由于我们是要遍历上三角矩阵的所有元素，那么这很显然就需要用到上三角矩阵和主对角线的元素坐标关系了吗，上文我们知道了上三角矩阵和主对角线元素坐标的关系是在某一行中，二者行坐标相同，而列坐标一定是上三角矩阵元素的列坐标小于主对角线元素的列坐标，所以就说明上三角矩阵的列坐标要小于同一行的主对角线元素的列坐标，那么主对角线元素的列坐标又有什么特征呢？其实很明显：主对角线的元素的坐标中的行和列都是相同的，是的，对于在某一行的主对角线元素来说，它的列坐标是和行坐标一样的，
那么这么一来，我们也就知道了，上三角矩阵的元素遍历，其的列坐标要小于同一行的主对角线元素的列坐标本质就是上三角矩阵的元素的列坐标要小于其在所在的行坐标。
由此，本题的第一种解法便已经搞定了，剩下的一些其余代码，相信大家必定是手拿把掐，所以这里就不再赘述，直接上完整代码：
#include <stdio.h>int main()
{int n;scanf("%d",&n);int arr[100][100] = { 0 };for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){scanf("%d",&arr[i][j]);}}int flag = 1;for (int i = 1; i <= n; i++){for (int j = 1; j < i; j++){if (arr[i][j] != 0){flag = 0;break;//发现就终止循环，避免多余时间浪费}}}if (flag == 1){printf("YES");}else{printf("NO");}return 0;
}接下来我们讲一下方法二：
方法二：
其实这个方法二，本质还是在第一个方法的基础上，我们依然需要这幅图：
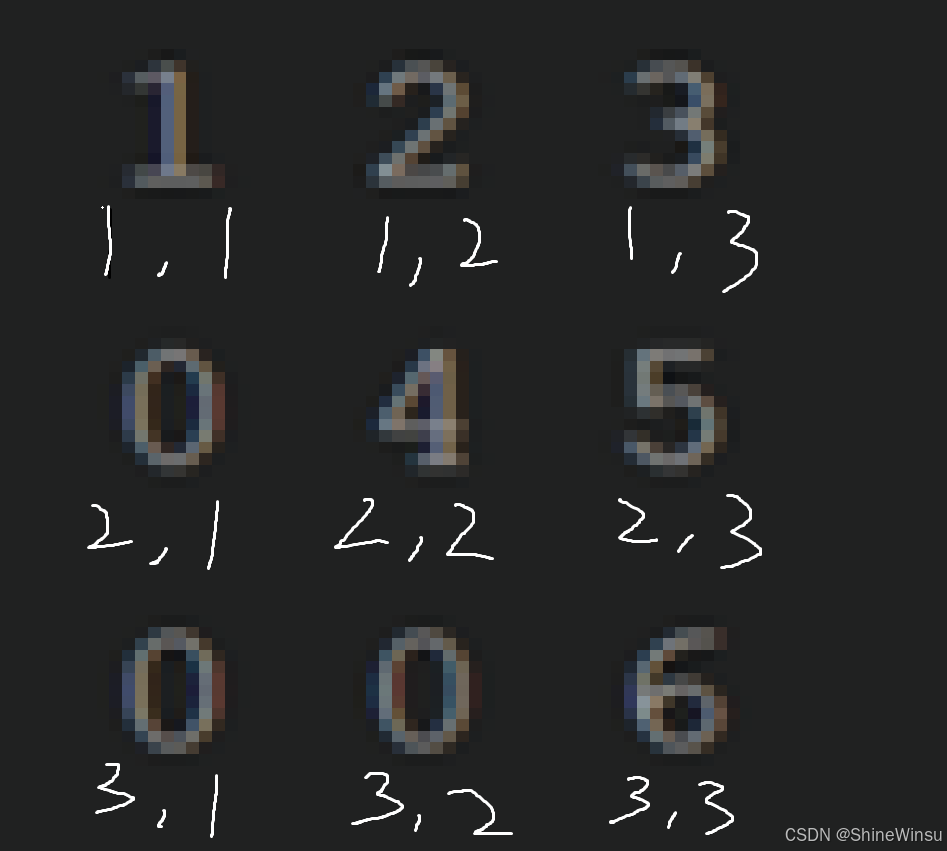
经过方法一我们知道，上三角矩阵的元素遍历，其的列坐标要小于同一行的主对角线元素的列坐标本质就是上三角矩阵的元素的列坐标要小于其在所在的行坐标。
而在方法一中，我们是通过修改列j的限制条件实现这一目的，那么有没有什么办法，不用修改列j的限制条件就能实现这一目的呢？有的有的，且看下文
既然我们知道上三角矩阵的元素的列坐标要小于其所在那一行的行坐标，那我们直接在遍历二维数组的所有元素时加一个判断条件，要求只有当某个元素的列坐标小于其行坐标时，在进行判断其是否为0，如此一来，便也可以实现我们的目的了，下面给出完整代码：
#include <stdio.h>int main() {int n = 0;int i = 0;int j = 0;int flag = 1; // 先假设是上三角矩阵，初始化为1scanf("%d", &n);int arr[n][n];for (i = 0; i < n; i++) {for (j = 0; j < n; j++) {scanf("%d", &arr[i][j]);}}for (i = 0; i < n; i++) {for (j = 0; j < n; j++) {if (i > j) {if (arr[i][j]!= 0) {flag = 0; // 发现不符合条件的元素，将标志变量设为0break; // 跳出内层循环，不用再检查这一行后面的元素了}}}if (flag == 0) { // 如果已经确定不是上三角矩阵，跳出外层循环，不用检查后面的行了break;}}if (flag == 1) {printf("YES\n");} else {printf("NO\n");}return 0;
}如上。
再给上一版详细注释：
#include <stdio.h> // 引入标准输入输出库，让程序能够使用scanf(输入)和printf(输出)函数// 主函数：C语言程序必须有一个main函数，程序从这里开始执行
int main() {// 定义变量并初始化：int n = 0; // 用于存储矩阵的阶数（行数和列数相同，因为是方阵）int i = 0; // 循环变量，用于表示行索引int j = 0; // 循环变量，用于表示列索引int flag = 1; // 标志变量：1表示"是上三角矩阵"，0表示"不是"，先假设是上三角矩阵// 读取矩阵的阶数n：// scanf函数格式：%d表示读取整数，&n表示将读取到的整数存入变量n的地址// 例如输入"3"，表示要判断的是3x3的方阵scanf("%d", &n);// 定义一个n行n列的二维数组arr，用于存储矩阵元素// 这里使用了C99标准的变长数组（VLA）特性，数组大小由运行时输入的n决定// 注意：如果编译器不支持VLA，可能需要改为固定大小（如int arr[100][100];）int arr[n][n];// 读取矩阵的所有元素：// 外层for循环：控制行数，i从0到n-1（C语言数组索引从0开始）// 例如n=3时，i会取0、1、2，分别对应第1行、第2行、第3行for (i = 0; i < n; i++) {// 内层for循环：控制列数，j从0到n-1// 例如n=3时，j会取0、1、2，分别对应第1列、第2列、第3列for (j = 0; j < n; j++) {// 读取一个整数，存入arr数组的第i行第j列// 例如i=0,j=1表示第1行第2列的位置scanf("%d", &arr[i][j]);}}// 核心逻辑：检查是否为上三角矩阵// 上三角矩阵的数学定义：主对角线（i==j的位置）以下的元素（i>j的位置）必须全为0// 主对角线：从左上角(0,0)到右下角(n-1,n-1)的对角线// 外层循环：遍历每一行for (i = 0; i < n; i++) {// 内层循环：遍历当前行的每一列for (j = 0; j < n; j++) {// 判断当前元素是否在主对角线下方：行索引i > 列索引j// 例如i=2,j=1：第3行第2列，在主对角线下方if (i > j) {// 检查主对角线下方的元素是否为0// 如果发现有一个元素不等于0，说明不是上三角矩阵if (arr[i][j]!= 0) {flag = 0; // 将标志变量设为0，表示"不是上三角矩阵"break; // 跳出内层循环，当前行剩余元素无需检查}}// 注意：主对角线（i==j）和上方（i<j）的元素可以是任意值，无需检查}// 如果已经确定不是上三角矩阵（flag=0），就跳出外层循环，无需检查后续行if (flag == 0) {break;}}// 根据flag的值输出判断结果：if (flag == 1) {// flag保持1，说明所有主对角线下方的元素都是0，是上三角矩阵printf("YES\n"); // 输出YES并换行} else {// flag变为0，说明存在主对角线下方的元素不为0，不是上三角矩阵printf("NO\n"); // 输出NO并换行}return 0; // main函数返回0，表示程序正常结束
}到这里，我们便对这一道题大功告成了。
BC139 矩阵交换：
这道题，说难不算难，说简单也算不上多简单，所以，我们还是先看题目：
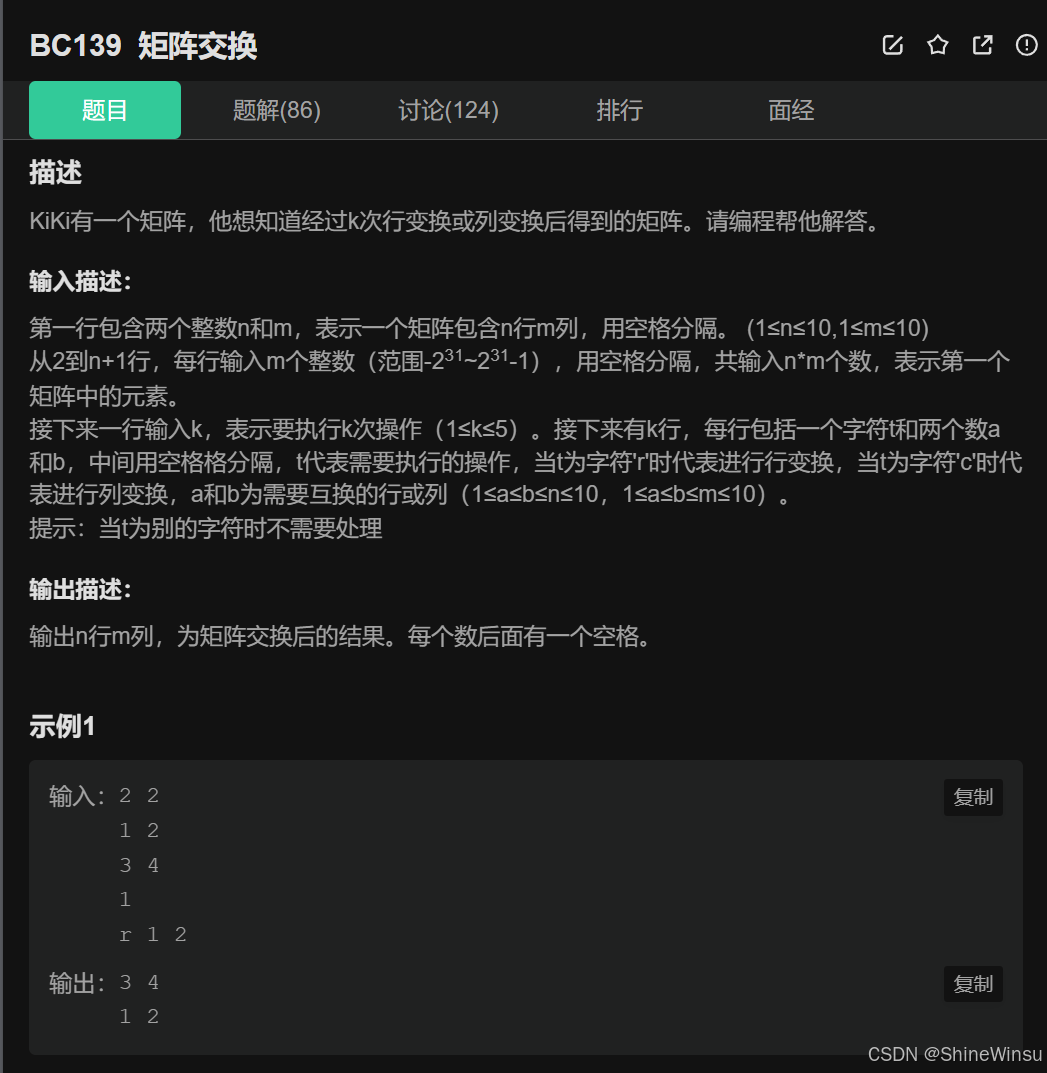
题意分析：
这道题的核心是对矩阵进行指定次数的行变换或列变换操作。
输入部分
- 首先输入两个整数 n 和 m，分别表示矩阵的行数和列数（1≤n≤10，1≤m≤10）。
- 接着输入 n 行，每行 m 个整数，构成原始矩阵。
- 然后输入一个整数 k，表示要执行的操作次数（1≤k≤5）。
- 最后输入 k 行操作指令，每行包含一个字符 t（代表操作类型，t=′r′ 为行变换，t=′c′ 为列变换）和两个整数 a、b（代表要交换的行或列，1≤a≤b≤n（行变换时），1≤a≤b≤m（列变换时））。
处理逻辑
根据每次操作的类型 t，对矩阵进行相应的行或列交换：
- 若 t=′r′，则交换矩阵的第 a 行和第 b 行。
- 若 t=′c′，则交换矩阵的第 a 列和第 b 列。
- 若 t 为其他字符，无需处理。
输出部分
输出经过 k 次操作变换后的矩阵，每行的每个数后有一个空格。
继续解答：
知道了题意之后，我们对于各个变量的输入应该已经烂熟于心了，我这里便直接给出输入各个参数的代码：
int n, m;
scanf("%d%d", &n, &m);
int arr[100][100] = {0};// 读取矩阵元素（行和列从1开始计数）
for (int i = 1; i <= n; i++)
{for (int j = 1; j <= m; j++) {scanf("%d", &arr[i][j]);}
}char t = 0;
int a, b;
int k = 0;
scanf("%d",&k);
while (k--)
{scanf(" %c %d %d", &t, &a, &b);
}在这里强调一下，由于我们有进行字符的输入，为了避免空格或者回车吸收为字符，我们要在%c前面加一个空格，表示忽略回车或者空格，详情见这篇博客：对字符、字符函数、scanf、sprintf的详细解析(对于实现字符串左旋以及右旋的分析暨判断字符串是否是某个字符串左旋或右旋所实现)-CSDN博客
接下来，我们的重头戏便是要解决对矩阵的行交换或者列交换。
我们先来解决行交换：
解决行交换：
还是那句话，当我们没有思路的时候，就去标元素坐标，这里也是，我们把没进行行交换的各个元素坐标标出，再去把进行了行交换的各个元素的坐标标出，然后再把这二者相同元素的坐标进行各自比较，如下是对题目所给示例进行1 2行交换：
| 元素值 | 交换前坐标 | 交换后坐标 | 坐标变化分析 |
|---|---|---|---|
| 1 | (1,1) | (2,1) | 行号从 1 变为 2，列号 1 保持不变 |
| 2 | (1,2) | (2,2) | 行号从 1 变为 2，列号 2 保持不变 |
| 3 | (2,1) | (1,1) | 行号从 2 变为 1，列号 1 保持不变 |
| 4 | (2,2) | (1,2) | 行号从 2 变为 1，列号 2 保持不变 |
我们观察一下，进行行交换的时候，元素的列坐标是不变的，而行坐标则是互相交换，你要就交换1 2行的元素，那就列坐标不变，行坐标互相交换，即由arr[1][j]变为arr[2][j]，不过大家要注意，arr[1][j]变为arr[2][j]这一步只是把第二行的元素变到第一行去，我们还得实现把第一行的元素变到第二行去呢，那么问题来了，众所周知，编译器运行代码是从上到下依次运行，而经过了arr[1][j]变为arr[2][j]之后，数组的第一行已经变成了原本数组的第二行，也就是说，此时的数组第一行和第二行都一样，之前的第一行已经烟消云散了，那我们还怎么进行把原本的第一行元素变到第二行去呢？
诶，大家不必忧愁，其实很简单，俗话说得好，此处不留爷，自有留爷处，我们再创建一个数组temp去1:1的拷贝原数组，然后再在进行交换的时候，改为arr[1][j]=temp[2][j]，这么一来，temp数组中的元素该是什么样还是什么样，并不会发生元素改变，不用担心会出现上面的情况，随后我们的arr[2][j]变为arr[1][j]也是可以借助temp数组轻松实现，就如这样：arr[2][j]=temp[1][j]，下面是实现行交换的完整代码：
if (t == 'r') // 行交换操作
{for (int j = 1; j <= m; j++){arr[a][j] = temp[b][j];arr[b][j] = temp[a][j];}
}解决了行交换之后，我们就要解决列交换了
解决列交换：
其实列交换和行交换类似，我们依然看比图：
| 元素值 | 交换前坐标 | 交换后坐标 | 坐标变化分析 |
|---|---|---|---|
| 1 | (1,1) | (2,1) | 行号从 1 变为 2，列号 1 保持不变 |
| 2 | (1,2) | (2,2) | 行号从 1 变为 2，列号 2 保持不变 |
| 3 | (2,1) | (1,1) | 行号从 2 变为 1，列号 1 保持不变 |
| 4 | (2,2) | (1,2) | 行号从 2 变为 1，列号 2 保持不变 |
我们观察一下，进行列交换的时候，元素的行坐标是不变的，而列坐标则是互相交换，你要交换1 2列的元素，那就行坐标不变，列坐标互相交换，即由arr[i][1]变为arr[i][2]，而对于列交换，我们要要使用temp数组进行交换，即与行交换类似。下面是实现列交换的完整代码：
if (t == 'c') // 列交换操作
{for (int i = 1; i <= n; i++) // 遍历每一行{// 交换第a列和第b列的元素arr[i][a] = temp[i][b];arr[i][b] = temp[i][a];}
}注意事项：
经过上文，我们已经知道了如何实现行交换以及列交换，并且知道了要通过临时数组temp去进避免进行交换一行/列后，无法继续交换的问题。
但是掘解决完上述这些，还不够，大家可以看到题目说可能会进行多次行/列交换，那么问题来了，当进行了一次行交换之后，我们的arr数组是变了，可是temp数组没变，而在进行下一次行/列交换时，我们依然需要temp数组，而按道理来说，进行下一次行/列交换时，要在上一次交换后的基础上，去进行新的交换，也就是要对改变后的arr数组进行交换，可是我们的temp数组却是没有变化，依旧是最开始的样子，没有相应的变为改变后的arr数组，那么我们要怎么解决这个问题呢？
其实也很简单，我们只需要在进行行/列交换之后，就再次把arr数组全盘拷贝到temp数组中，即进行一次交换之后，我们把temp数组中的元素也进行更新，令其等于交换后的arr数组，这么一来，我们便能完美解决这个问题，下面是完整代码：
// 处理行交换操作
if (t == 'r')
{// 交换第a行和第b行的所有元素for (int j = 1; j <= m; j++){arr[a][j] = temp[b][j];arr[b][j] = temp[a][j];}// 更新临时矩阵temp，保持与当前arr一致for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j];}}
}// 处理列交换操作
if (t == 'c')
{// 交换第a列和第b列的所有元素for (int i = 1; i <= n; i++){arr[i][a] = temp[i][b];arr[i][b] = temp[i][a];}// 更新临时矩阵temp，保持与当前arr一致for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j];}}
}大功告成：
到了这里，这一题便算是大功告成了，下面我便给出完整代码：
#include <stdio.h>int main()
{int n, m;scanf("%d%d",&n,&m);int arr[100][100] = { 0 };for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &arr[i][j]);}}int temp[100][100] = { 0 };//创建一个相同数组存储for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j];}}char t = 0;int a, b;int k = 0;scanf("%d",&k);while (k--){scanf(" %c %d %d", &t, &a, &b);if (t == 'r'){for (int j = 1; j <= m; j++){arr[a][j] = temp[b][j];arr[b][j] = temp[a][j];}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j];//进行一次更换后，就得对temp数组更新，不难temp一直是最初的arr}}}if (t == 'c'){for (int i = 1; i <= n; i++){arr[i][a] = temp[i][b];arr[i][b] = temp[i][a];}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j];}}}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%d ",arr[i][j]);}printf("\n");}return 0;
}再给上一版详细注释：
#include <stdio.h> // 引入标准输入输出库，用于实现数据的输入和输出功能// 主函数：程序从这里开始执行，是整个程序的入口
int main()
{// 定义两个整数变量n和m，分别用来存储矩阵的行数和列数// 变量命名规则：n是number of rows的缩写，m是number of columns的缩写int n, m;// 从键盘读取两个整数，分别存入n和m中// scanf函数的作用是从标准输入（通常是键盘）读取数据// "%d%d"是格式控制字符串，表示要读取两个十进制整数// &n和&m是变量的地址，表示将读取到的数据存储到n和m的内存地址中// 例如：如果输入"2 3"，则n的值会变成2（2行），m的值会变成3（3列）scanf("%d%d", &n, &m);// 定义一个二维数组arr，用于存储原始矩阵的数据// 数组大小为100x100，这是因为题目中规定n和m的最大值都是10// 100x100的大小远大于题目要求，这样定义可以确保数组不会越界// = {0}表示对数组进行初始化，将所有元素都设置为0（C语言特性）int arr[100][100] = {0};// 外层for循环：用于遍历矩阵的每一行，i表示当前行号// i从1开始，到n结束（因为题目中行列编号是从1开始计数的）// 例如：n=2时，i会取1和2，分别表示第1行和第2行for (int i = 1; i <= n; i++){// 内层for循环：用于遍历当前行的每一列，j表示当前列号// j从1开始，到m结束// 例如：m=3时，j会取1、2、3，分别表示第1列、第2列、第3列for (int j = 1; j <= m; j++){// 从键盘读取一个整数，存储到arr数组的第i行第j列// &arr[i][j]表示arr数组第i行第j列元素的内存地址// 例如：当i=1,j=2时，就是读取数据到第1行第2列的位置scanf("%d", &arr[i][j]);}}// 定义一个临时二维数组temp，作用是保存矩阵当前的状态// 为什么需要临时数组？// 因为在交换行或列时，如果直接操作原数组arr，会导致原始数据被覆盖// 例如：交换第1行和第2行时，如果先把第2行的数据放到第1行，// 那么第1行的原始数据就丢失了，再想把第1行数据放到第2行就做不到了// 所以需要先用temp保存当前状态，交换时从temp中读取原始数据int temp[100][100] = {0};// 将原始矩阵arr中的所有元素复制到临时矩阵temp中// 确保temp和arr在初始状态下完全相同for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j]; // 把arr[i][j]的值赋给temp[i][j]}}// 定义操作相关的变量：// t：字符类型，用于存储操作类型，'r'表示行交换，'c'表示列交换// a和b：整数类型，用于存储要交换的行号或列号（题目规定a≤b）// k：整数类型，用于存储需要执行的操作总次数char t = 0;int a, b;int k = 0;// 从键盘读取操作次数k// 例如：输入"2"表示接下来要执行2次交换操作scanf("%d", &k);// while循环：执行k次操作// k--是后置递减运算符，先判断k是否大于0，再将k的值减1// 例如：初始k=2时，第一次循环判断k=2>0，执行循环体，然后k变成1；// 第二次循环判断k=1>0，执行循环体，然后k变成0；// 第三次判断k=0，循环结束，正好执行2次操作while (k--){// 从键盘读取一次操作的指令// 格式字符串" %c %d %d"的含义：// - 开头的空格：用于跳过输入缓冲区中可能存在的换行符或空格// （因为上一次输入可能按下了回车键，缓冲区中会残留'\n'）// - %c：读取一个字符（操作类型t）// - %d：读取一个整数（a的值）// - %d：读取一个整数（b的值）// 例如：输入"r 1 2"，表示t='r'，a=1，b=2，即交换第1行和第2行scanf(" %c %d %d", &t, &a, &b);// 判断操作类型是否为行交换（t等于'r'）if (t == 'r'){// 行交换逻辑：交换第a行和第b行的所有元素// 循环遍历每一列（j从1到m），依次交换对应列的元素for (int j = 1; j <= m; j++){// 第一步：将temp中第b行第j列的元素值赋给arr中第a行第j列// 为什么用temp而不是arr？因为temp中保存的是交换前的原始数据arr[a][j] = temp[b][j];// 第二步：将temp中第a行第j列的元素值赋给arr中第b行第j列// 这时候即使arr[a][j]已经被修改，也不影响，因为我们用的是temp中的原始值arr[b][j] = temp[a][j];}// 行交换完成后，必须更新临时矩阵temp// 因为下一次操作需要基于当前最新的矩阵状态进行// 如果不更新temp，下一次交换会使用旧的矩阵数据，导致结果错误for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j]; // 把更新后的arr数据复制到temp}}}// 判断操作类型是否为列交换（t等于'c'）if (t == 'c'){// 列交换逻辑：交换第a列和第b列的所有元素// 循环遍历每一行（i从1到n），依次交换对应行的元素for (int i = 1; i <= n; i++){// 第一步：将temp中第i行第b列的元素值赋给arr中第i行第a列arr[i][a] = temp[i][b];// 第二步：将temp中第i行第a列的元素值赋给arr中第i行第b列arr[i][b] = temp[i][a];}// 列交换完成后，同样需要更新临时矩阵temp// 确保下一次操作使用的是最新的矩阵状态for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){temp[i][j] = arr[i][j]; // 把更新后的arr数据复制到temp}}}}// 所有操作执行完毕后，输出最终的矩阵// 外层for循环：遍历每一行for (int i = 1; i <= n; i++){// 内层for循环：遍历当前行的每一列for (int j = 1; j <= m; j++){// 输出arr[i][j]的值，后面跟一个空格// 题目要求"每行的每个数后有一个空格"，这里严格按照要求实现printf("%d ", arr[i][j]);}// 一行的所有元素输出完毕后，打印一个换行符// 确保下一行的元素从新的一行开始输出printf("\n");}// main函数返回0，表示程序正常结束。return 0;
}由此，本题完结撒花。
结语：
写到这里，BC136 和 BC139 这两道二维数组的中等题就彻底讲解完毕了。回头再看这两道题，从最初拿到题目时可能有的 “无从下手”，到一步步拆解题意、标注坐标找规律、用临时数组解决数据覆盖问题，其实整个过程就像在拆解一个复杂的拼图 —— 看似零散的知识点，只要耐心梳理，总能找到串联起来的逻辑线。
比如判断上三角矩阵时，我们从 “主对角线下方元素全为 0” 这个定义出发，先通过表格列出元素坐标，才发现 “i>j” 这个隐藏的遍历条件；而矩阵交换题里，最关键的 “临时数组更新” 问题，也是在想到 “第一次交换后原数组已改变，下次交换需基于新状态” 时才豁然开朗。这些细节其实都在告诉我们：编程里没有天生的 “难题”，只有没被拆解开的 “小问题”。
可能有同学会说，刚开始写这类题时，总会漏掉一些细节 —— 比如忘记在 %c 前加空格导致字符输入出错，或者交换行 / 列时没更新临时数组导致后续操作出错。但请别担心，这些 “踩坑” 的经历其实是最宝贵的。我在最初学二维数组时，也曾因为没搞懂 “0 行 0 列还是 1 行 1 列” 的索引问题，反复调试了好几遍代码；也曾因为没及时 break 跳出循环，导致程序做了很多无用功。但正是这些调试的过程，让我对 “如何让代码更高效、更严谨” 有了更深的理解。
二维数组作为编程入门阶段的 “小难点”，其实是在为我们后续学习更复杂的数据结构（比如二维链表、图）打基础。今天我们在这两道题里用到的 “通过坐标找规律”“用标志变量记录状态”“用临时变量保存原始数据” 的思路，未来在解决更难的问题时依然会用到。就像盖房子，现在掌握的这些 “小技巧”，都是将来搭建更复杂程序的 “砖瓦”
最后想跟大家说：学习编程从来不是 “一蹴而就” 的事情。可能今天看懂了这两道题，但下次遇到类似的变形题还是会卡顿；可能第一次写代码时要对着注释一步步走，但多写几遍就能熟练掌握。没关系，慢慢来就好。每一次对着题目发呆后的豁然开朗，每一次调试成功后的小小喜悦，都是在慢慢靠近 “会编程、能解决问题” 的目标。
下一篇博客，我们会继续讲解二维数组剩下的几道中等题，难度可能会稍有提升，但我相信，只要跟着 “拆解题意 — 找规律 — 写代码 — 调 bug” 的节奏走，大家一定能稳步拿下。也期待在评论区看到大家分享自己的解题思路，或者遇到的问题 —— 编程路上，我们一起加油，一起在代码的世界里慢慢成长！
诸君共勉！！！