使用AdaLoRA 自适应权重矩阵微调大模型介绍篇

前言：AdaLoRA解决了LoRA低秩参数r的人工选择问题，并且实现动态调整模型所有关键部分（包括FFN）,全面提升模型能力

LoRA的问题

​ LoRA可以不改变原始模型的参数，而是训练一个“小补丁”（低秩矩阵 ΔW），把它加在原来的模型上（W = W₀ + ΔW）。这样只需要训练这个小补丁，大大节省了计算资源。但存在问题待解决

• 固定秩（r）不够灵活：LoRA 要求你事先决定这个“小补丁”的复杂度（称为“秩 r”）。但不同层、不同任务需要不同的复杂度，统一设置可能要么浪费参数，要么导致无法微调出最好效果。统一分配参数预算不合理。
• 只调整 Attention 部分，忽略了 FFN（前馈网络）：LoRA 默认只对自注意力层（Attention）做微调，但模型中的前馈网络（FFN）也非常重要，忽略它可能限制模型的表现。

AdaLoRA介绍

AdaLoRA 的核心思想是：智能地、自适应地分配参数预算，把更多的参数用在“更重要的地方”，解决了LoRA存在的问题

具体实现原理包括：

• 使用 SVD 分解代替低秩矩阵：AdaLoRA 使用奇异值分解（SVD）来表示增量更新 ΔW，奇异值分解比人为的方法肯定好，SVD 可以将矩阵分解为三个部分： U Σ Vᵀ，其中 Σ 是一个对角矩阵，表示每个维度的重要性（奇异值越大越重要），这样我们就可以根据重要性动态调整每个参数，关于奇异值分解见文章末尾SVD推导介绍

• 重要性评分 + 动态剪枝：AdaLoRA 根据SVD奇异值和训练过程中的梯度信息为每个参数（或每组参数）计算一个“重要性分数”，判断它对新任务有多大贡献。像园丁修剪树枝一样：重要的保留甚至加强，不重要的剪掉（参数设为0）。这样就实现了在不同层、不同模块中动态分配参数预算，而不是一刀切。

• 同时微调 Attention 和 FFN：AdaLoRA 不再只关注 Attention，而是对模型中所有关键部分（包括 FFN）都进行微调，全面提升模型适应新任务的能力。

形象比喻：全参数微调，把整栋楼重新装修一遍，费时费钱。LoRA给每个房间都贴同一款墙纸，不管房间用途，AdaLoRA先评估每个房间的重要性：客厅用贵墙纸，卫生间用防水漆，储物间简单刷白——既省钱又效果好

SVD 分解代替低秩矩阵

1、计算重要性评分

AdaLoRA 对参数进行重要性建模，并将其与 SVD 分解结合起来的。这个过程是 AdaLoRA 相比 LoRA 更智能的核心所在。

AdaLoRA 认为，一个参数的重要性 s(w) 取决于两个方面：

1. 敏感性 I(w)：这个参数对最终效果的影响有多大？变化一点，损失函数会不会剧烈变化？
2. 不确定性 U(w)：我们对这个参数的敏感性评估有多大的把握？它的值是稳定还是波动很大？
   
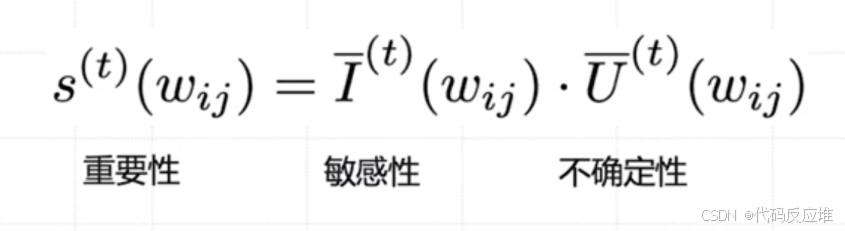
   敏感性衡量的是：改变这个参数，会对模型的损失函数造成多大影响。：敏感性 ≈ 权重值 * 梯度值。这就像评估一个员工的影响力，既要看他本身的职位高低，也要看他的工作是否处在关键路径上

为了防止训练过程中敏感性的剧烈波动，AdaLoRA 使用滑动平均来平滑每一轮的敏感性值，使其更稳定。这里的 β₁ 是一个超参数（如0.99），用于控制历史值的权重。

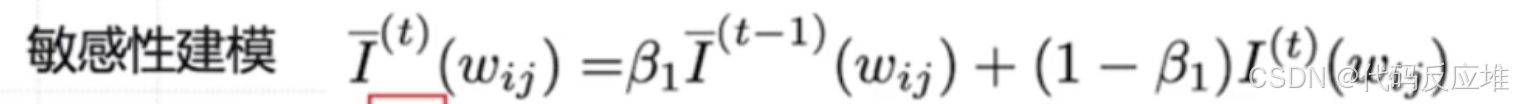
不确定性衡量的是：我们对上面计算的敏感性值有多大的信心。如果某一参数的敏感性在每次训练迭代中变化很大，说明我们的评估很不稳定，不确定性就高。如果它很稳定，不确定性就低。

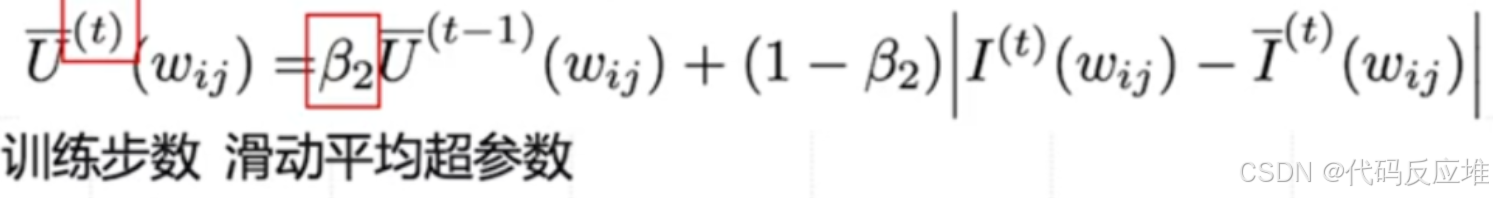
最终，将平滑后的敏感性 I(w) 和不确定性 U(w) 相乘，就得到了该参数的最终重要性评分 S(w)。

2、将重要性评分代入SVD

LoRA 将增量更新 ΔW 分解为两个小矩阵 B 和 A (ΔW = B A)，并平均地优化它们。

AdaLoRA 则更精细，AdaLoRA 使用SVD的三元组替代了LoRA的二元组，它将 ΔW 用 SVD 分解，AdaLoRA 不是平等地对待 SVD 分解后的所有参数，而是为每一个SVD三元组****计算一个总的重要性评分，这个总评分由以下三部分组成：**

• **奇异值 λ 本身的重要性评分。这是最重要的部分，因为奇异值直接代表了该维度的重要性。
• 左奇异向量 P 的所有参数的平均重要性评分
• 右奇异向量 Q 的所有参数的平均重要性评分
  
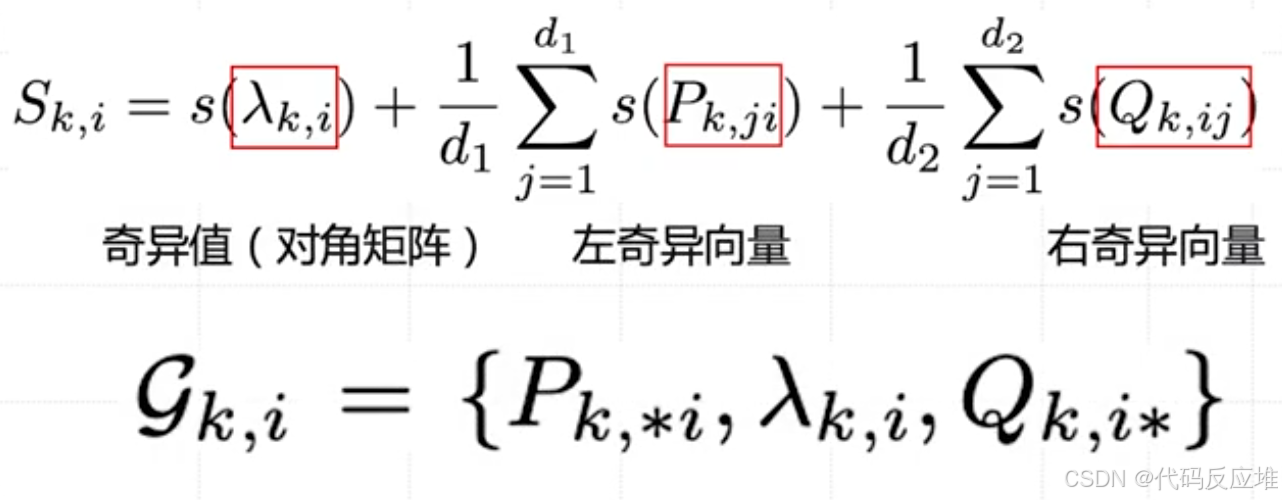
  这样做的目的是：不仅仅看奇异值 λ 本身重不重要，还要看支持这个“重要方向”的向量 P 和 Q 的参数们是否也重要。这是一个更全面、更稳健的评估。

动态剪枝微调

1、设定目标

AdaLoRA 不是在盲目地优化，而是在遵守数学规则（保持矩阵正交性）的前提下，努力降低模型的误差。

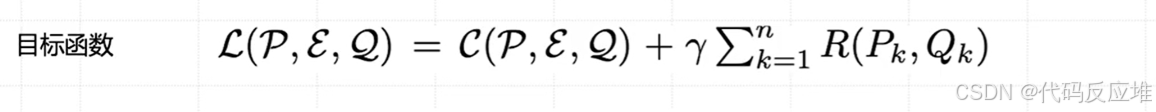
• L(P, E, Q)：是其整个优化过程的目标函数，代表了模型当前状态的“成本”或“不好”的程度
• 𝐶(𝑃,𝐸,𝑄)：主要目标，最小化模型预测损失。即损失函数Loss。这是一个在机器学习中非常标准的概念。
• 𝑅(𝑃𝑘,𝑄𝑘)：正则项，保证左奇异向量矩阵 P 和右奇异向量矩阵 Q 的正交性（团队协作规范），目的是维持数值稳定性，保证 SVD 分解的结构有效性，从而使得重要性评分和剪枝操作更加可靠。
• 𝛾：控制正则项权重的超参数。是一个权重系数。它控制了正则化项 R 相对于主损失 C 的重要性。
  • 如果 γ = 0，AdaLoRA 就完全不管正交性，只追求任务性能，这可能导致训练不稳定。
  • 如果 γ 太大，AdaLoRA 会过于强调保持正交性，可能会牺牲任务性能。
  • 因此，γ 需要一个合适的值来平衡两者。简单说：γ \* Σ R(P_k, Q_k) 回答的问题是——“模型参数的结构是否优雅、稳定？”

2、初始化训练(初始阶段)

在最初阶段，AdaLoRA 和 LoRA 差不多，都是在正常地训练和更新参数，即通过梯度下降来调整给它们的资源（奇异值 Λ）。

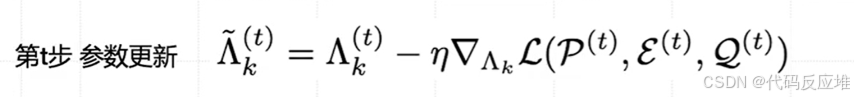
3、模型剪枝(中期阶段)

计算重要性评分S,评估了三元组的重要性（奇异值 λ 的大小）、稳定性（不确定性）和影响力（敏感性）。

对所有三元组按 评分 从大到小排序。

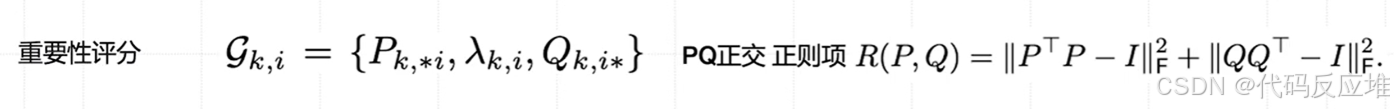
当到达时间t时，收集所有重要性评分，只保留排名在前 b^{(t)}，其他的进行资源回收 ,将排名靠后的、不重要的三元组整个移除（将其奇异值 λ 设为0）。这相当于收回了分配给这些方向的参数预算，再分配：将收回的预算重新分配给那些重要性评分高的三元组，甚至允许重要的矩阵创建新的三元组（增加秩 r）。

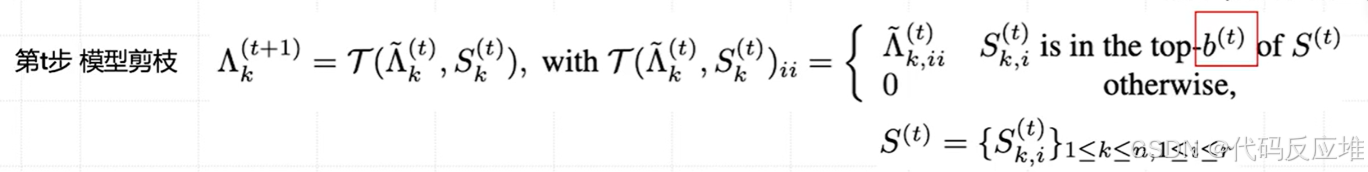
4、稳定阶段

预算会固定在一个较低的水平 b^{(T)}进行最后的冲刺和最终微调。这叫 稳定阶段。确保模型收敛并稳定性能。

5、各阶段的预算调度

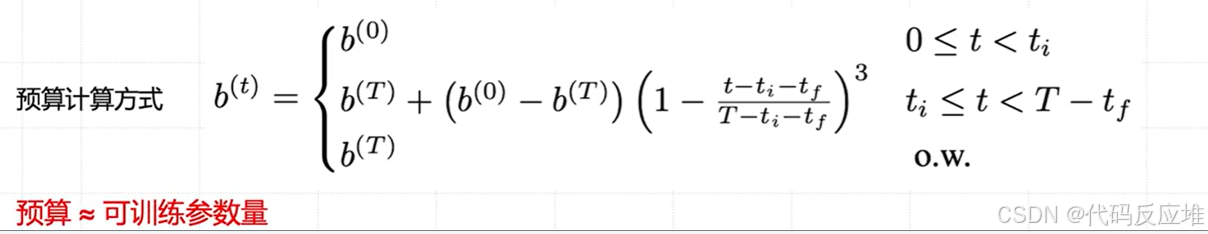
• 初始阶段（0≤𝑡<𝑡<ti）：高预算 𝑏(0)，广泛探索。
• 衰减阶段（𝑡𝑖≤𝑡<T−tf）：非线性缩减预算，聚焦重要方向，知道了哪些是重要方向，开始逐渐地、非线性地缩减总预算，淘汰的力度越来越大，越来越聚焦，自适应调整秩 r，增加重要方向其对应的奇异值 λ 的数值。由于不重要方向的奇异值被置零，其有效的“本征秩” r 降低了；而重要方向的奇异值变得更大，其有效的“重要性”提高了。这就实现了在不同权重矩阵间动态、自适应地分配参数预算。
• 稳定阶段（𝑡≥T−tf）：固定低预算 b(T)，最终微调，确保模型收敛并稳定性能。

AdaloRA实验数据

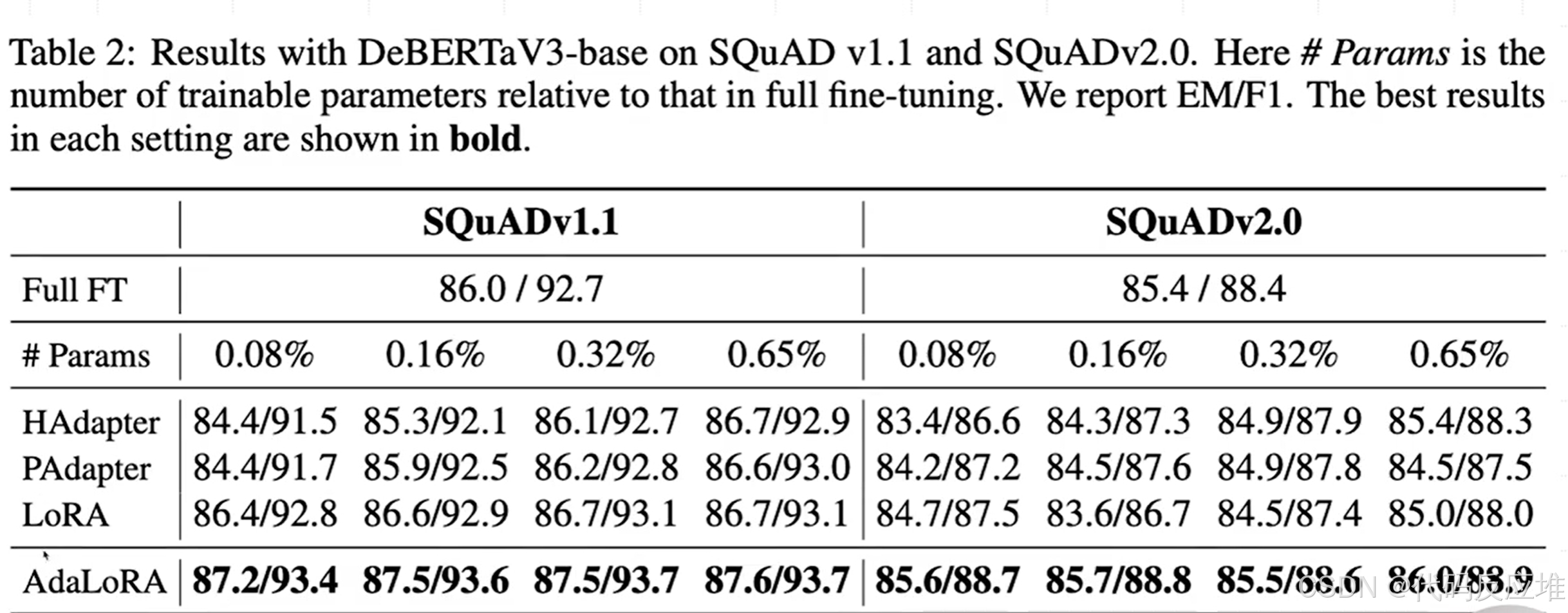
任务说明：SQuAD 是一个机器阅读理解任务，模型需要根据文章回答问题。EM (Exact Match) 和 F1 分数是评估指标，越高越好。

1. 碾压性优势：在所有参数量设置下（0.08%, 0.16%, 0.32%, 0.65%），AdaLoRA 的 EM 和 F1 分数全面超过了传统的全量微调 (Full FT) 和其他的高效微调方法（HAdapter, PAdapter, LoRA）。这在实践中是惊人的结果，意味着用不到 1% 的参数就能获得更好的性能。
2. 对比 LoRA：直接对比 AdaLoRA 和 LoRA 行，可以清晰看到 AdaLoRA 的稳定优势。例如，在 SQuADv1.1 上，即使 AdaLoRA 只用 0.08% 的参数（87.2/93.4），也显著优于使用 0.65% 参数的 LoRA（86.7/93.1）。这证明了自适应分配参数比简单固定秩分配要高效得多。
3. 参数利用效率：对于 AdaLoRA，增加参数量（从 0.08% 到 0.65%）带来的性能提升非常小，说明它在极低的参数量下就已经接近其性能上限。而其他方法（如 LoRA）则更需要依赖更多的参数来提升效果。

结论：在阅读理解任务上，AdaLoRA 在参数效率和最终效果方面都做到了最佳。

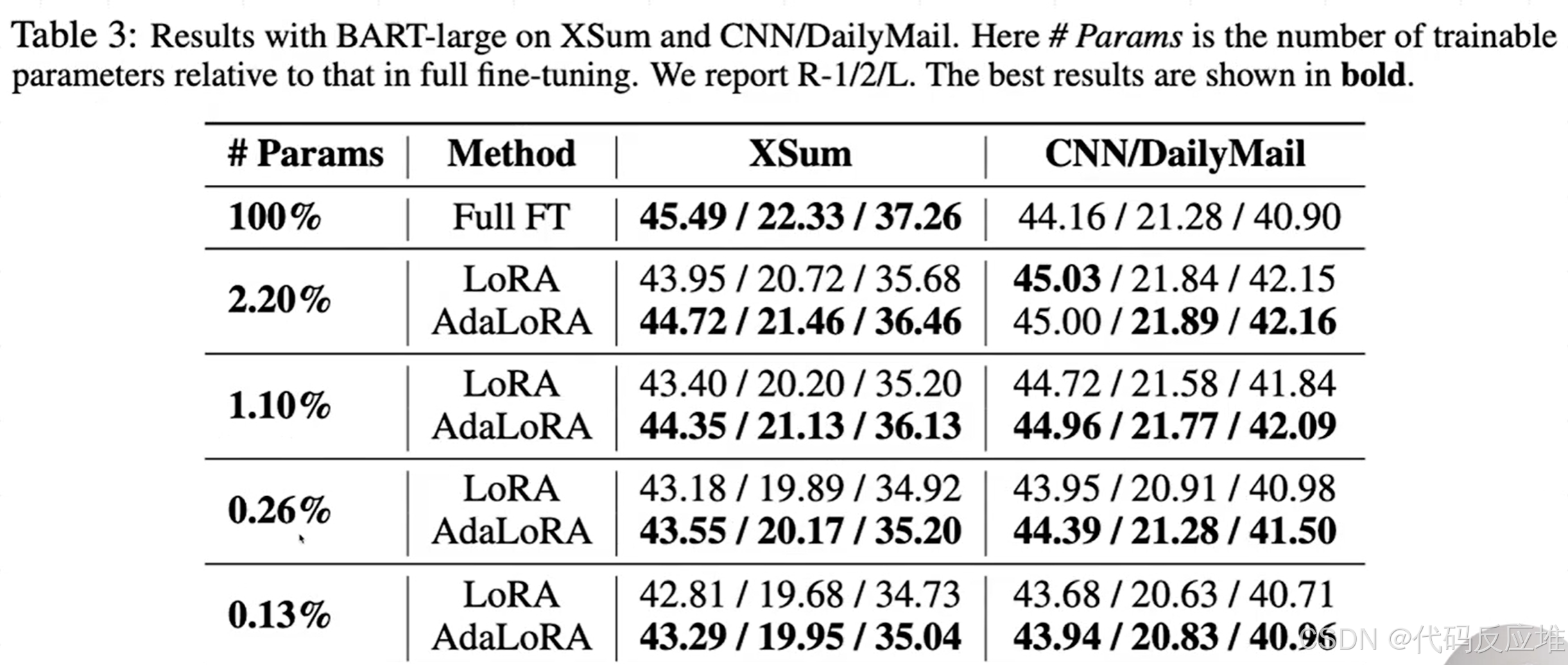
任务说明：文本摘要任务要求模型生成更短的精炼摘要。使用 ROUGE-1, ROUGE-2, ROUGE-L 作为评估指标，越高越好。

1. 全面领先：在与 LoRA 的直接对比中，AdaLoRA 在 几乎所有参数量设置和所有数据集上均取得了更高的 ROUGE 分数。这证明了 AdaLoRA 的优势不仅限于分类或阅读理解任务，在生成任务上同样有效。
2. 低预算下的显著优势：参数量越少，AdaLoRA 的优势往往越明显。例如，在 XSum 数据集上，当参数量仅为 0.13% 时，AdaLoRA 的 ROUGE-L 为 35.04，而 LoRA 为 34.73。这个差距在低资源场景下是非常有价值的提升。
3. 超越全量微调：在 CNN/DailyMail 数据集上，仅用 2.2% 参数的 AdaLoRA 和 LoRA 就已经超过了全量微调 (44.16/21.28/40.90) 的效果。这再次凸显了参数高效微调方法的巨大潜力。

结论：在文本摘要任务上，AdaLoRA 同样证明了其卓越的有效性和参数效率。

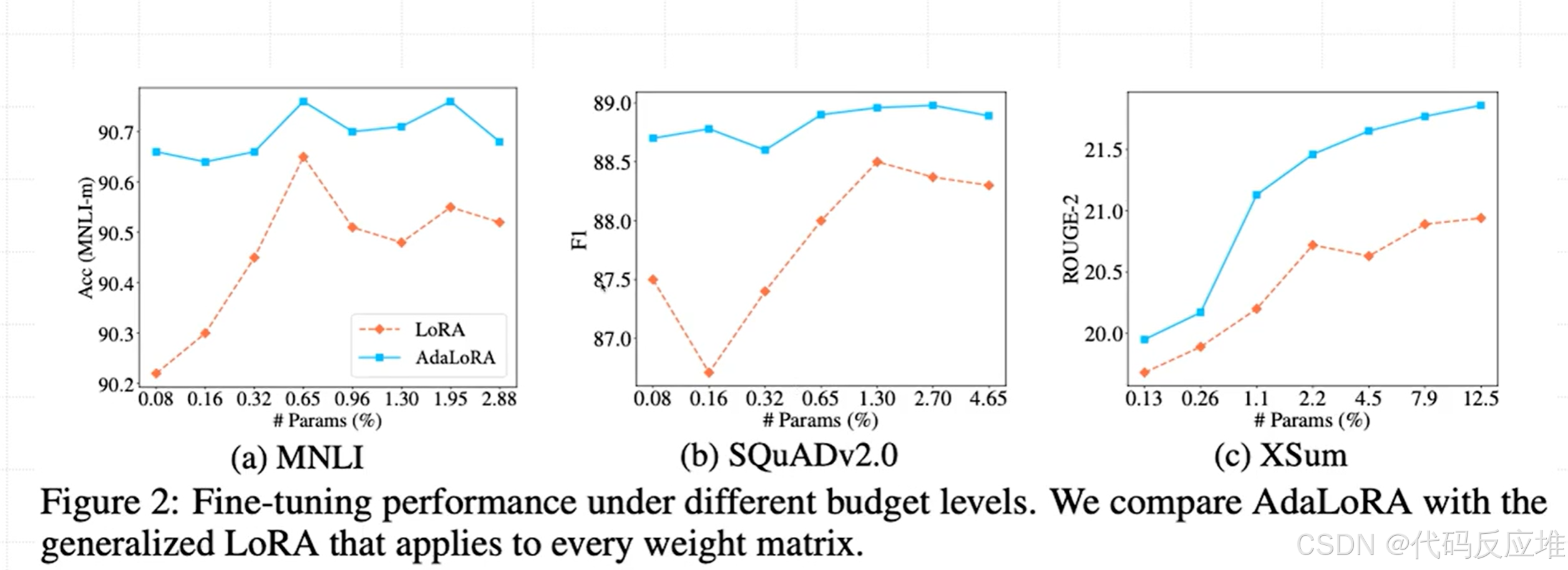
图表说明：这条曲线展示了随着可训练参数量（预算）的增加，模型性能（准确率/F1）的变化趋势。

数据解读：

1. 全局优势：AdaLoRA 的曲线始终位于 LoRA 曲线上方。这意味着在任何预算水平下，选择 AdaLoRA 都能获得比 LoRA 更好的性能。
2. 边际效益：可以看到，两条曲线在参数达到一定量后都会进入“平台期”，增加参数带来的收益变小。但 AdaLoRA 的平台期来得更早、位置更高。这说明 AdaLoRA 能用更少的参数达到“饱和性能”。
3. 低预算差距最大：在预算非常低的最左侧，两条曲线的差距最大。这证明 AdaLoRA 的自适应预算分配策略在参数极度受限的场景下优势最为明显，因为它能确保每一分参数都用在刀刃上。

结论：该图从趋势上直观证明了 AdaLoRA 相对于固定秩方法的全面优势。

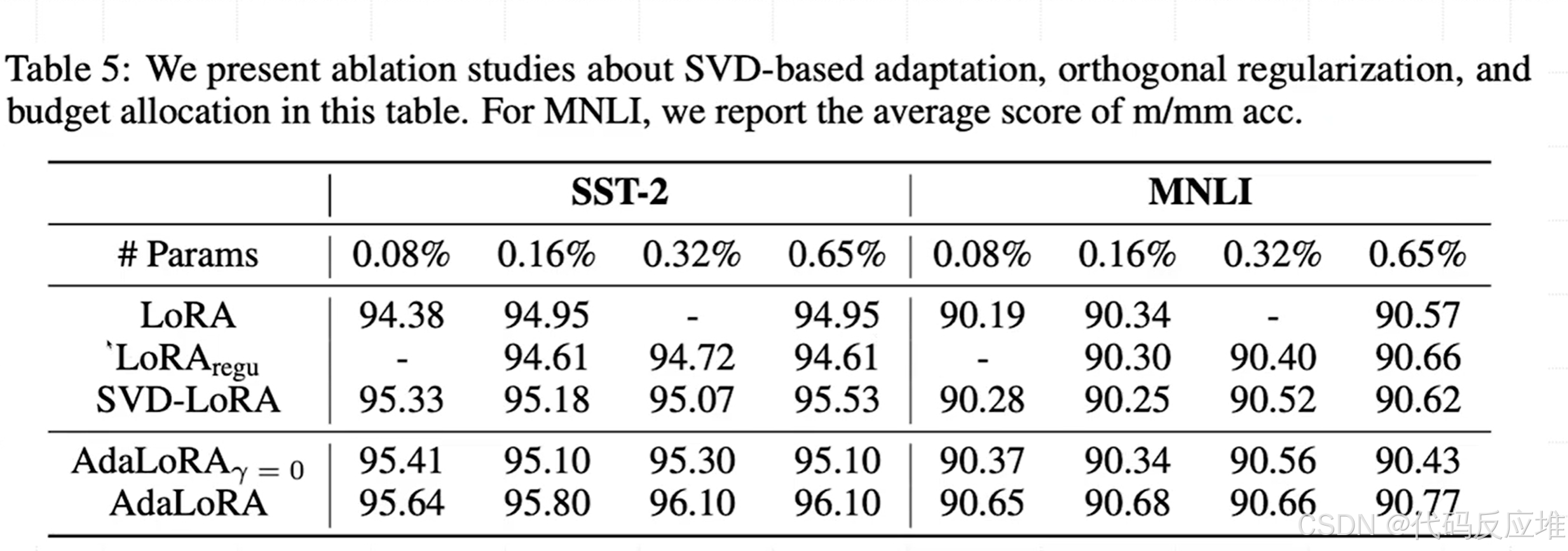
实验说明：消融实验是为了验证 AdaLoRA 各个设计组件（SVD形式、正交约束、动态预算分配）是否都是必要的，以及各自的贡献有多大。

• LoRA: 原始 LoRA 方法。
• LoRAregu: 给 LoRA 加上正交约束。
• SVD-LoRA: 使用 SVD 形式但不做动态分配（固定秩）。
• AdaLoRA(γ=0): 使用 SVD 形式和动态分配，但去掉正交约束。
• AdaLoRA: 完整版 AdaLoRA。

数据解读：

1. 正交约束的重要性：比较 AdaLoRA(γ=0) 和 AdaLoRA，可以看到加上正交约束 (γ≠0) 后，性能在大多数情况下都有稳定提升。这证明了维持奇异向量的正交性对于稳定性很重要。
2. 动态分配的核心作用：比较 SVD-LoRA 和 AdaLoRA，AdaLoRA 显著更强。这说明仅仅是使用 SVD 形式（而不是BA）带来的提升有限，真正的性能增益主要来自于动态的预算分配策略。
3. 组合的力量：完整的 AdaLoRA 几乎在所有设置下都是最好的，表明SVD形式、正交约束和动态分配三者结合才是最优解。

结论：消融实验证实了 AdaLoRA 的每一个设计都不是多余的，它们共同作用才达成了最佳效果。

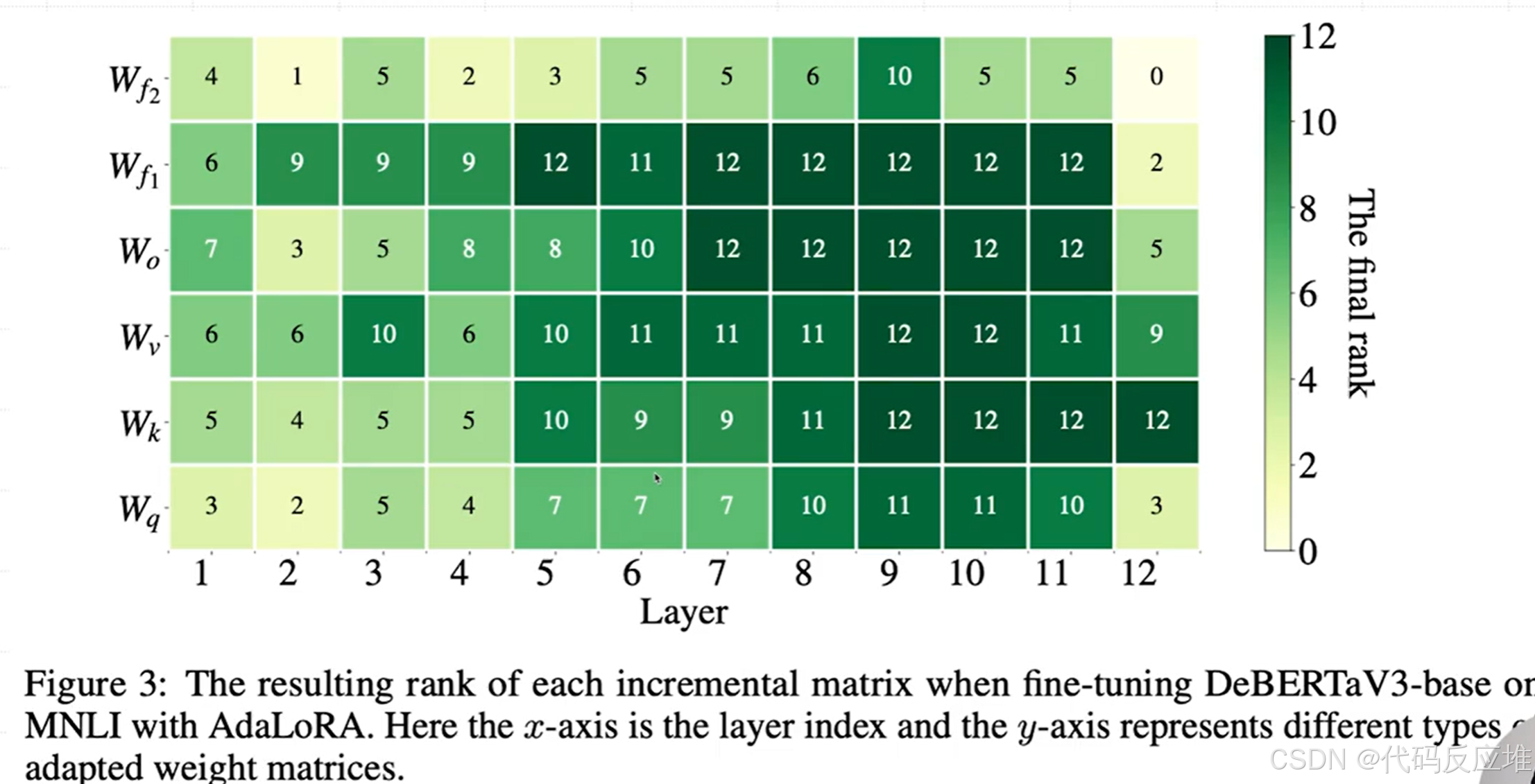
图表说明：这张热力图展示了在微调结束后，DeBERTa 模型不同层（x轴）、不同权重矩阵（y轴）最终分配到的秩（颜色越深，秩越大）。

数据解读：

1. 动态分配而非平均分配：AdaLoRA 没有为所有矩阵分配相同的秩。例如，W_f1 和 W_f2 (FFN层的两个权重矩阵) 获得的平均秩较高，而 W_q, W_k, W_v (注意力层的投影矩阵) 获得的平均秩较低。这符合一个普遍先验：FFN 层通常比注意力层蕴含更多任务特定知识。
2. 层间差异：同一类型的矩阵在不同层分配到的秩也不同。这说明了不同层对下游任务的重要性确实是有差异的，而 AdaLoRA 成功捕捉到了这种差异。
3. 可视化验证：这张图是 AdaLoRA 核心思想的直接证据。它直观地告诉我们，AdaLoRA 确实在实践中学到了“好钢用在刀刃上”的策略，而不是纸上谈兵。

结论：该图从实证角度证实了 AdaLoRA 能够智能地、自适应地为不同参数的增量矩阵分配不同的重要性（体现为不同的秩）。

SVD推导介绍

0、介绍

假设我们有2个用户（Alice, Bob）给2部电影（战狼1、战狼2）打分，可以看作是维度。

评分矩阵 A 则是一个n *n = 2x2 的矩阵, 这样nxn的矩阵又称为方阵，只有方阵才能计算特征值，如果是mxn的矩阵，SVD会拆解成两个方阵mxm、nxn去计算。

以下例子基于nxn方阵讲解

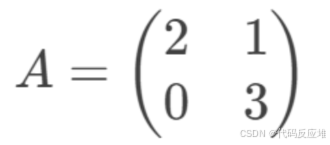
使用SVD进行分解该矩阵A = U Σ Vᵀ 。分析这个矩阵：每一行相当于是一个数据样本记录，这里就有两行样本

将每个值想象成某种特征（电影）的强度值（是否好看），如2代表的是战狼1好看度为2

1、Vᵀ 计算（右奇异向量）

含义：为在列空间坐标系上的最小单位上的一个基础单位矩阵

计算列空间矩阵（计算A的转置矩阵乘以A矩阵（矩阵相乘想象成 “行乘列” 的游戏，第一个矩阵的第一行和第二个矩阵的第一列数分别相乘后相加2×2+0×0=4得到结果矩阵里第一行第一列的数4，接着第一行乘以第二列2×1+0×3 = 2，以此类推））

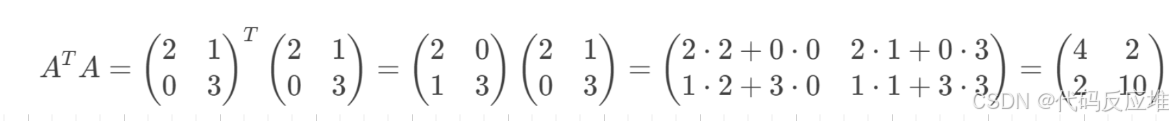
**根据列空间矩阵计算列空间上的基础单位矩阵Vᵀ **

**先计算特征值：**已知当满足A v = λ v，我们称λ 为矩阵A的特征值、v为矩阵A的特征向量
λ 是一个数，而 v 是一个nx1的n行1列矩阵。计算时需要将λ转换成矩阵形式，可以将它乘以一个单位矩阵（单位矩阵是主对角线上元素都是1，其余元素都是0）即可。
最终得到式子：(A−λI)v=0
要想使特征向量v存在，必须满足det(A−λI)=0称为特征方程，可求出λ

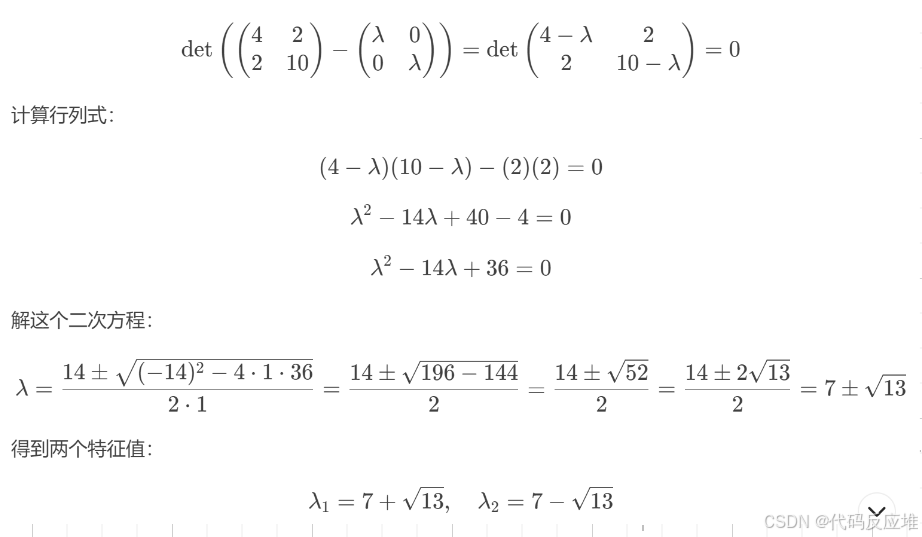
对于一个 n × n 的方阵，它的特征方程 det(A - λI) = 0 是一个关于 λ 的 n 次多项式方程（称为特征多项式）
根据代数基本定理，一个 n 次多项式方程在复数域内恰好有 n 个根因此，一个 n × n 的矩阵确实有 n 个特征值。

再计算对应的特征向量单位化最终得到基础单位矩阵Vᵀ：

​ 矩阵转置在乘以自己后生成的矩阵，称为实对称矩阵，其不同特征值所对应的特征向量，是相互正交的即在几何上是垂直的。如果将这些特征向量进行单位化，那么称它们为一组标准正交基，可以将标准正交的特征向量直接作为矩阵的列，构成的矩阵称为正交矩阵V，在AdaLoRA中，这个矩阵 V 的列指示了参数更新中重要的“方向”。

​ 单位化目的：就是把原来的特征向量变成长度为1的向量，1的模长利用勾股定理的思路，得出模后将矩阵中各数除以模值，其实就是等比例缩小值，比例是由类似勾股定理计算得出的

2、计算Σ（奇异值）

含义：每个特征的缩放操作，可以表示每个特征的重要性

构造奇异值矩阵Σ

3、计算U（左奇异向量）

含义: 为在行空间坐标系上的最小单位上的一个基础单位矩阵（特征之间的相似度），确保结果已正确的方式呈现以便使用

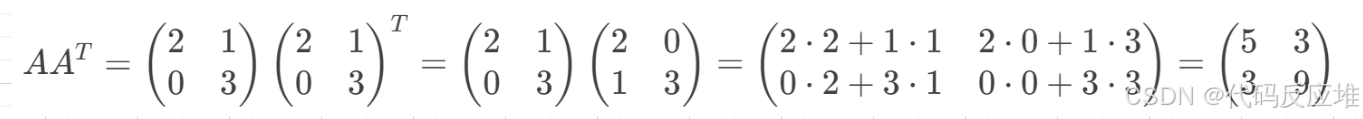
以上用记录的不同特征的所有强度相乘，如果值越接近，说明这两个记录对所有电影的评分非常相似，同理类似求正交矩阵转置Vᵀ一样计算，但是有一个关键的数学结论可以简便计算：数学结论得出AAᵀ和 AᵀA 拥有完全相同的非零特征值，一旦已知 vᵢ 和 σᵢ可以直接用如下公式计算得出单位向量

4、最终结果与验证

A = U Σ Vᵀ