当前位置：首页 > news >正文

线段树相关算法题（5）

news 2025/8/31 13:52:58

hello大家好，今天是2025年8月25日，我来给大家分享两道线段树相关的算法题。这两道算法题都涉及线段树 + 剪枝操作，学过线段树的朋友们可以来挑战一下。

前言（预备知识）

线段树在维护区间修改过程中，有些操作是无法“懒”下来的，比如：对整个区间的每一个数执行开根号操作。这时只能从上往下把所有的点全部修改。但是，如果在修改的过程中发现，整个区间在修改到一定程度的时候，整个区间就无需修改。那么，就可以通过剪枝操作，优化区间的修改。这样的线段树也叫势能线段树。

题目一：上帝造题的七分钟 2

题目链接：上帝造题的七分钟 2

1：题目描述

2：算法原理

分析题目：这道题涉及数组的区间修改和区间查询操作，我们往线段树上考虑。

但是，区间中所有的数开根号这一操作是没有办法“懒”下来的。

因为，修改之后的 sum 值和修改之前的 sum 值没有明显关系（推不出关系来）。

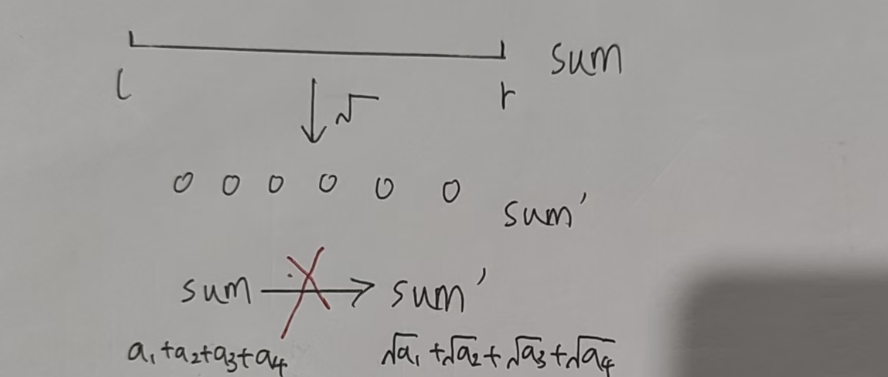
“懒”不下来的话我们只能老老实实地递归，但是这样的话时间复杂度就会过高。

每一次递归的话都要递归到叶子节点（只有一个数）才能进行修改操作。sum' = sqrt(sum);

这样的话，一共有 n 个叶子节点，树高为 log n 一次修改操作的时间复杂度就是O（n log n）

（还不如直接遍历区间修改O（n））m 次修改操作时间复杂度为 O（m n log n）。

但是我们发现：如果在递归的过程中出现了区间中最大值为 1 的区间，就没必要再递归下去了，

因为 sqrt（1）= 1。我们可以再这里进行剪枝操作。就可以极大的优化时间复杂度。

1e12 进行 6 次开根号操作也就变为1了，所以加上这一个剪枝操作之后，时间复杂度就降下来了。就按向下 6 层来算，时间复杂度也就仅仅为O（6 * n * log n）。

分析线段树：

结构体 node 中多存储一个 max 信息为后面的剪枝操作做准备。

其余基本上都是线段树的模板，这里就不再过多赘述了。

3：代码实现

#include <iostream>
#include <cmath>using namespace std;#define lc p << 1
#define rc p << 1 | 1
typedef long long LL;const int N = 1e5 + 10;int n, m;
LL a[N];struct node
{int l, r;LL sum, max;
}tr[N << 2];void pushup(int p)
{tr[p].sum = tr[lc].sum + tr[rc].sum;tr[p].max = max(tr[lc].max, tr[rc].max);
}void build(int p, int l, int r)
{tr[p] = {l, r, a[l], a[l]};if(l == r) return;int mid = (l + r) >> 1;build(lc, l, mid); build(rc, mid + 1, r);pushup(p);
}void modify(int p, int x, int y)
{//剪枝if(tr[p].max == 1) return;int l = tr[p].l, r = tr[p].r;//递归到叶子节点再修改 if(l == r){tr[p].sum = sqrt(tr[p].sum);tr[p].max = sqrt(tr[p].max); return;}int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, y);if(y > mid) modify(rc, x, y);pushup(p);
}LL query(int p, int x, int y)
{	 int l = tr[p].l, r = tr[p].r;if(x <= l && r <= y){return tr[p].sum;}int mid = (l + r) >> 1;LL ret = 0;if(x <= mid) ret += query(lc, x, y);if(y > mid) ret += query(rc, x, y);return ret;
}int main()
{cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];build(1, 1, n);cin >> m;while(m--){int op, l, r; cin >> op >> l >> r;if(l > r) swap(l, r);if(op == 0) modify(1, l, r);else cout << query(1, l, r) << endl;}return 0;
}

题目二：The Child and Sequence

题目链接：The Child and Sequence

1：题目描述

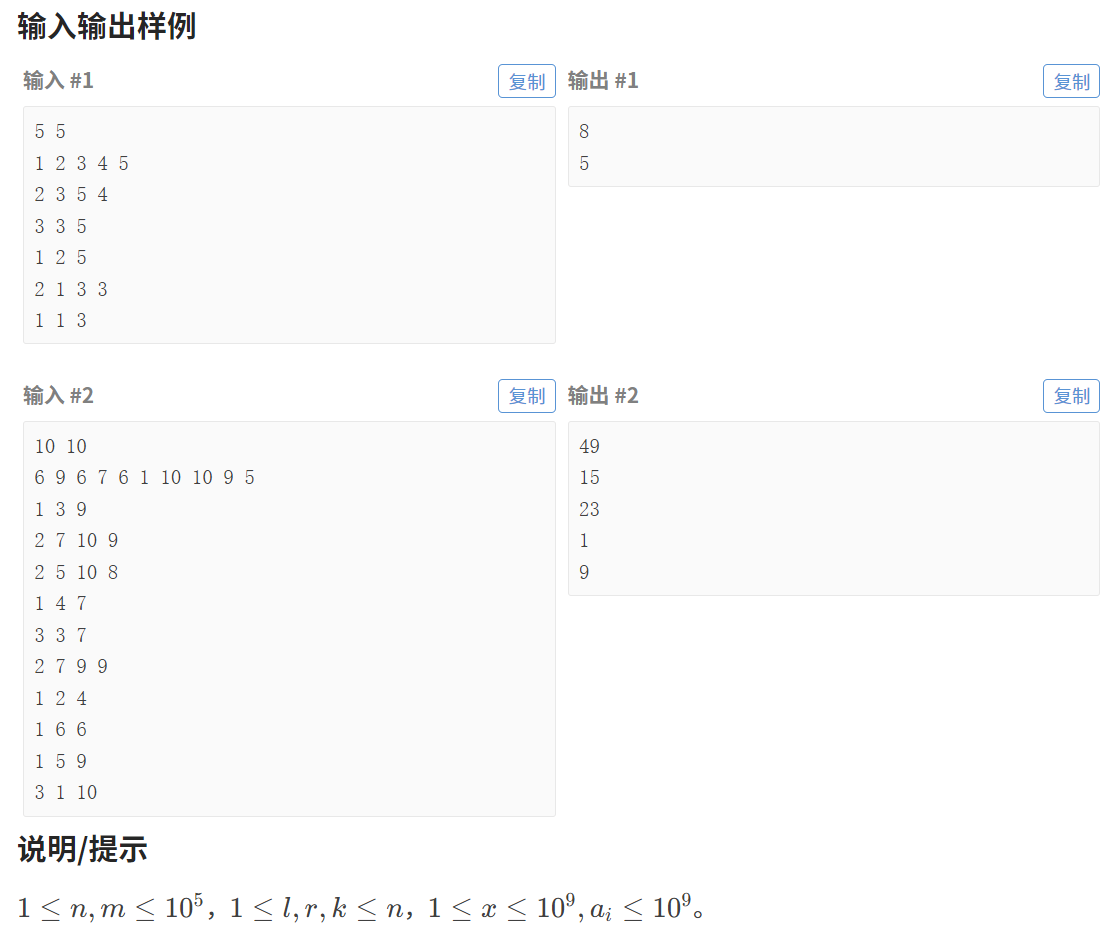
2：算法原理

这道题涉及区间修改、单点修改和区间查询操作，往线段树上考虑。

本题和上一题类似，同样是区间求该操作没有办法“拦下来”。我们仍然可以通过剪枝操作优化时间复杂度。

3：代码实现

#include <iostream>using namespace std;#define lc p << 1
#define rc p << 1 | 1
typedef long long LL;
const int N = 1e5 + 10;int n, m;
int a[N];struct node
{int l, r;LL sum, max;
}tr[N << 2];void pushup(int p)
{tr[p].sum = tr[lc].sum + tr[rc].sum;tr[p].max = max(tr[lc].max, tr[rc].max);
}void build(int p, int l, int r)
{tr[p] = {l, r, a[l], a[l]};if(l == r) return;int mid = (l + r) >> 1;build(lc, l, mid); build(rc, mid + 1, r);pushup(p);
}void modify(int p, int x, int y, int mod)
{//剪枝 if(tr[p].max < mod) return;int l = tr[p].l, r = tr[p].r;//递归到叶子节点修改 if(l == r){tr[p].max = tr[p].max % mod;tr[p].sum = tr[p].sum % mod;return;}int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, y, mod);if(y > mid) modify(rc, x, y, mod);pushup(p);
}void modify2(int p, int x, int y)
{//单点修改int l = tr[p].l, r = tr[p].r;if(l == x && r == x){tr[p].sum = y;tr[p].max = y; return;} int mid = (l + r) >> 1;if(x <= mid) modify2(lc, x, y);else modify2(rc, x, y);pushup(p);
}LL query(int p, int x, int y)
{int l = tr[p].l, r = tr[p].r;if(x <= l && r <= y){return tr[p].sum;}int mid = (l + r) >> 1;LL ret = 0;if(x <= mid) ret += query(lc, x, y);if(y > mid) ret += query(rc, x, y);return ret; 
} int main()
{cin >> n >> m;for(int i = 1; i <= n; i++) cin >> a[i];build(1, 1, n);while(m--){int op, l, r, x; cin >> op >> l >> r;if(op == 1) cout << query(1, l, r) << endl;else if(op == 2){cin >> x;modify(1, l, r, x);}else modify2(1, l, r);}return 0;
}

好的，今天的分享就先到这里了！！！如果大家有疑问的话，欢迎下来和我进行交流~~

查看全文

http://www.dtcms.com/a/359166.html