简说DDPM

---

1. 基础过程FP和RP

1.1 前向过程FP(forward process or diffusion process)

以图像为例，前向过程就是从一副干净的图像，逐步加噪最后变成一副近似完全噪声的图像；
这个过程认为是符合Markov过程的，所以从概率上来讲：
$$\begin{array}{c}q(x_T,x_{T-1}...x_1|x_0)=q(x_T|x_{T-1})q(x_{T-1}|x_{T-2})...q(x_1|x_0)=\prod _{t=1}^{T}q(x_t|x_{t-1})\end{array}$$

对于其中任意一步 $q(x_t|x_{t-1})$，根据加噪的方式，可以有明确的表达；当噪声符合Gaussian时，则
$$\begin{array}{c}{X}_t=\sqrt{1-{\beta }_t}{X}_{t-1}+{\sqrt{\beta }}_t{ϵ}_t\end{array}$$
其中${ϵ}_t$是Gaussian噪声，所以
$$\begin{gathered} X_t\sim N(\sqrt{1-{\beta }_t}{X}_{t-1},{\beta }_{t}I) \\ q(x_t|x_{t-1})=\frac{1}{\sqrt{2\pi {\beta }_t}}exp\left(-\frac{{\left(x_t-X_{t-1}\right)}^2}{2{\beta }_t}\right) \end{gathered}$$

1.1.1 FP 概率的递归

根据式(2)，为了表示方便，可以令 ${\alpha }_t=1-{\beta }_t$ ，递归代入可得
$$\begin{array}{c}\begin{array}{rl}{X}_t& =\sqrt{{\alpha }_t}{X}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =\sqrt{{\alpha }_t}(\sqrt{{\alpha }_{t-1}}{X}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{ϵ}_{t-1})+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{X}_{t-2}+\sqrt{{\alpha }_t(1-{\alpha }_{t-1})}{ϵ}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\end{array}\end{array}$$
观察公式(3)的后两项，可以令
$$\begin{array}{rl}Z& =\sqrt{{\alpha }_t(1-{\alpha }_{t-1})}{ϵ}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =\sqrt{1-{\alpha }_t{\alpha }_{t-1}}ϵ\end{array}$$

解释：两个Gaussian分布的叠加是一个新的Gaussion分布，且生成新的分布的方差为两个分布方差的和；有严格的证明，此处略

则依次递归可得
$$\begin{array}{rl}{X}_t& =\sqrt{{\alpha }_t}{X}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_t\\ & =...\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}...{\alpha }_1}{X}_{t0}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}...{\alpha }_1}{ϵ}_t\end{array}$$
为了表示方便，我们记 $\overline{{\alpha }_t}={\alpha }_t{\alpha }_{t-1}...{\alpha }_1$，则有
$$\begin{array}{c}{X}_t=\sqrt{\overline{{\alpha }_t}}{X}_0+\sqrt{1-\overline{{\alpha }_t}}{\widetilde{ϵ}}_t\end{array}$$

公式(4)表达了怎么直接获得第 t 次加噪效果的结果。

1.2 逆向过程RP(reverse process)

逆向过程表达了怎么通过去噪将一副噪声图逐步变成一副清晰的画面，类似的， 我们有以下表达：
$$\begin{array}{c}{p}_{\theta }(x_0,x_1...x_{T-1}|x_T)=p_{\theta }(x_{T-1}|x_T)p_{\theta }(x_{T-2}|x_{T-1})...p\theta (x_0|x_1)=\prod _{t=1}^T{p}_{\theta }(x_{t-1}|x_t)\end{array}$$

解释：$p_{\theta }$表达了由噪声图去噪的概率，下标$\theta$是未知参数，也就是我们需要获得的参数

2. Loss 计算

2.1 去噪目标

再思考一下Denoising的目的，是为了获得清晰的图片$x_0$，基于MLE的理论，也就是说，需要最大化$p_{\theta }(x_0)$的概率。这个时候我们一般会选择使用NLL作为loss，即
$$\tilde{\mathcal{L}}=\mathbb{E}[-log{p}_{\theta }(x_0)]$$
由于$x_0$的分布依赖$x_{1:T}$这些隐变量的分布，所以这里使用了常用的trick，即变分下界
$$\begin{array}{rl}\tilde{\mathcal{L}}& =\mathbb{E}[-log{p}_{\theta }(x_0)]\\ & \le {\mathbb{E}}_q\left[-\log \frac{p_{\theta }({\mathbf{x}}_{0:T})}{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}\right]\\ & ={\mathbb{E}}_q\left[-\log p({\mathbf{x}}_T)-\sum _{t\ge 1}\log \frac{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}{q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})}\right]=:\mathcal{L}\end{array}$$
我们对上式的Loss进行再变形，得到

$$\begin{array}{rl}\mathcal{L}& ={\mathbb{E}}_q\left[-\log \frac{p_{\theta }({\mathbf{x}}_{0:T})}{q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)}\right]\\ & ={\mathbb{E}}_q\left[-\log p({\mathbf{x}}_T)-\sum _{t\ge 1}\log \frac{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}{q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})}\right]\\ & ={\mathbb{E}}_q\left[-\log p({\mathbf{x}}_T)-\sum _{t>1}\log \frac{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}{q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})}-\log \frac{p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}{q({\mathbf{x}}_1|{\mathbf{x}}_0)}\right]\\ & ={\mathbb{E}}_q\left[-\log p({\mathbf{x}}_T)-\sum _{t>1}\log \frac{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)}\cdot \frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{q({\mathbf{x}}_t|{\mathbf{x}}_0)}-\log \frac{p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}{q({\mathbf{x}}_1|{\mathbf{x}}_0)}\right]\\ & ={\mathbb{E}}_q\left[-\log \frac{p({\mathbf{x}}_T)}{q({\mathbf{x}}_T|{\mathbf{x}}_0)}-\sum _{t>1}\log \frac{p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)}{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)}-\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)\right]\end{array}$$
再根据KL散度的定义，可以转化成
$$\begin{array}{c}\mathcal{L}={\mathbb{E}}_q\left[\underset{L_T}{\underbrace{D_{\mathrm{KL}}(q({\mathbf{x}}_T|{\mathbf{x}}_0)\parallel p({\mathbf{x}}_T))}}+\sum _{t>1}\underset{L_{t-1}}{\underbrace{D_{\mathrm{KL}}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t))}}\underset{L_0}{\underbrace{-\log p_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)}}\right]\end{array}$$

对于式(6)的通俗理解：

• $q({\mathbf{x}}_T|{\mathbf{x}}_0)$ 代表了已知的FP加噪过程，表示已知$x_0$得到$x_T$；
• 我们的目的是希望网络参数得到的概率分布 $p_{\theta }({\mathbf{x}}_{\mathbf{T}})$在未知${\mathbf{x}}_0$的条件下，与$q({\mathbf{x}}_T|{\mathbf{x}}_0)$尽可能接近
• 同理，$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$和$p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$也要尽可能接近；都表达了网络要学会在不知道$x_0$的前提下，学会估计出噪声分布

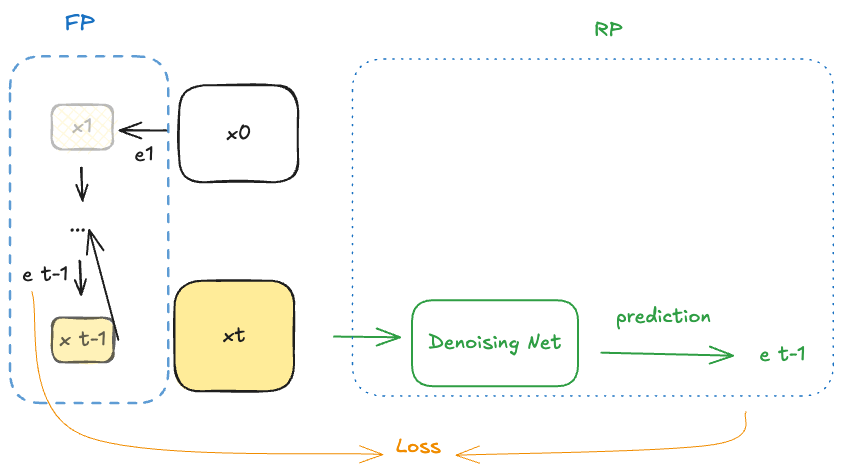
2.2 关键过程 $L_{t-1}$

在RP过程中，我们的重点是计算后验概率
$$p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))$$
其中的均值和方差是我们需要进行学习的，这里先忽略掉方差，先考虑均值。
令${\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t)={\sigma }_t^2$，则可以重写
$$\begin{array}{c}{L}_{t-1}={\mathbb{E}}_q\left[\frac{1}{2{\sigma }_t^2}\Vert {\tilde{\mathbf{\mu }}}_t({\mathbf{x}}_t,{\mathbf{x}}_0)-{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t){\Vert }^2\right]+C\end{array}$$
从上式可以看出一个基本点，就是我们的网络用来估计的均值${\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t)$的目标是尽可能的接近 ${\tilde{\mathbf{\mu }}}_t({\mathbf{x}}_t,{\mathbf{x}}_0)$，所以这个目标就是我们实际训练时的真值

继续，根据式(4)，可以将$x_0$替换为$x_t$的表达，即
$${\tilde{\mathbf{\mu }}}_t({\mathbf{x}}_t,{\mathbf{x}}_0)={\tilde{\mathbf{\mu }}}_t\left({\mathbf{x}}_t,\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ})\right)=\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)\right)$$
推导过程如下：
首先，$\tilde{\mu }$表示在已知$x_t,x_0$的情况下，$x_{t-1}$的分布或者概率，根据贝叶斯公式，有
$$q(x_{t-1}|x_t,x_0)=\frac{q(x_t,x_{t-1},x_0)}{q(x_t,x_0)}=\frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)\cancel{q(x_0)}}{q(x_t|x_0)\cancel{q(x_0)}}=\frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)}{q(x_t|x_0)}$$
而上式中的分子和分母都是已知的，并且根据加噪的假设，都是符合Gaussain分布的，以其中某一项举例
$$q(x_t|x_{t-1})=\frac{1}{\sqrt{2\pi {\beta }_t}}exp\left(-\frac{{\left(x_t-X_{t-1}\right)}^2}{2{\beta }_t}\right)$$
代入化简，可得均值即为
$${\tilde{\mu }}_t(x_t,x_0)=\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{{\beta }_t\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_t}{x}_0$$
所以，可有
$$\begin{array}{rl}{\tilde{\mu }}_t(x_t,x_0)& =\tilde{\mu }\left(x_t\left(x_0,ϵ\right),\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t(x_0,ϵ)-\sqrt{1-{\bar{\alpha }}_t}ϵ)\right)\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t\left(x_0,ϵ\right)+\frac{{\beta }_t\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t\left(x_0,ϵ\right)-\sqrt{1-{\bar{\alpha }}_t}ϵ)\\ & =\frac{{\alpha }_t(1-{\bar{\alpha }}_{t-1})}{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_t)}{x}_t\left(x_0,ϵ\right)+\frac{{\beta }_t(x_t\left(x_0,ϵ\right)-\sqrt{1-{\bar{\alpha }}_t}ϵ)}{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_t)}\\ & =\frac{1}{\sqrt{{\alpha }_t}}\left[\frac{({\alpha }_t-{\bar{\alpha }}_t+{\beta }_t)x_t\left(x_0,ϵ\right)}{1-{\bar{\alpha }}_t}-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}ϵ\right]\\ & =\frac{1}{\sqrt{{\alpha }_t}}\left[x_t\left(x_0,ϵ\right)-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}ϵ\right]\end{array}$$

经过以上的推导，我们的训练过程就可以表述为

2.3 深入理解$L_T$和$L_0$

（待完善）

---

---

Appendix A: 变分下界

可参考 变分下界

负对数似然（Negative Log-Likelihood, NLL）的变分下界（Variational Lower Bound），通常指的是证据下界（Evidence Lower BOund, ELBO）。它在变分推断（Variational Inference）中扮演着核心角色，用于近似复杂的概率分布。下面我将分步骤解释其概念、推导过程及直观理解。

1. 问题背景：为何需要变分下界？

假设我们有一个隐变量模型（如变分自编码器VAE），包含：

• 观测数据 $x$
• 隐变量 $z$（无法直接观测，如VAE中的潜在编码）

目标是最大化观测数据的对数似然 $\log p(x)$，但直接计算它通常不可行（因为需要积分：$p(x)=\int p(x|z)p(z)dz$）。因此，引入变分推断。

2. 变分下界的推导

为了近似真实的后验分布 $p(z|x)$，引入一个简单的可优化分布 $q_{\varphi }(z|x)$（如高斯分布），通过最小化两者的KL散度（$\text{KL}(q_{\varphi }(z|x)\Vert p(z|x))$）来逼近。

关键步骤：

从KL散度的定义出发：

$$\text{KL}(q_{\varphi }(z|x)\Vert p(z|x))={\mathbb{E}}_{q_{\varphi }(z|x)}\left[\log q_{\varphi }(z|x)-\log p(z|x)\right]$$

利用贝叶斯定理 $p(z|x)=\frac{p(x|z)p(z)}{p(x)}$，代入上式：

$$\begin{array}{rl}\text{KL}(q_{\varphi }(z|x)\Vert p(z|x))& ={\mathbb{E}}_{q_{\varphi }}\left[\log q_{\varphi }(z|x)-\log p(x|z)-\log p(z)+\log p(x)\right]\\ & ={\mathbb{E}}_{q_{\varphi }}\left[\log q_{\varphi }(z|x)-\log p(x|z)-\log p(z)\right]+\log p(x)\end{array}$$

整理后得到：

$$\log p(x)-\text{KL}(q_{\varphi }(z|x)\Vert p(z|x))={\mathbb{E}}_{q_{\varphi }}\left[\log p(x|z)+\log p(z)-\log q_{\varphi }(z|x)\right]$$

由于KL散度非负（$\text{KL}\ge 0$），因此：

$$\log p(x)\ge \underset{\text{ELBO}}{\underbrace{{\mathbb{E}}_{q_{\varphi }}\left[\log p(x|z)+\log p(z)-\log q_{\varphi }(z|x)\right]}}$$

这个下界就是ELBO（变分下界），即：

$$\text{ELBO}={\mathbb{E}}_{q_{\varphi }(z|x)}\left[\log p(x|z)\right]-\text{KL}(q_{\varphi }(z|x)\Vert p(z))$$

3. 如何理解ELBO？

ELBO由两部分组成：

1. 重构项 ${\mathbb{E}}_{q_{\varphi }}[\log p(x|z)]$：
   衡量从隐变量 $z$ 重构数据 $x$ 的质量（类似VAE中的解码器损失）。
2. KL正则项 $-\text{KL}(q_{\varphi }(z|x)\Vert p(z))$：
   迫使变分分布 $q_{\varphi }(z|x)$ 接近先验 $p(z)$（如标准高斯），防止过拟合。

直观解释：

• 最大化ELBO 等价于 最小化 $-\text{ELBO}$（即负对数似然的变分上界）。
• 由于 $\log p(x)\ge \text{ELBO}$，优化ELBO间接优化了真实的对数似然。

4. 与负对数似然的关系

• 直接最小化负对数似然 $-\log p(x)$ 不可行时，通过最大化ELBO来逼近。
• 在VAE中，损失函数 $\mathcal{L}=-\text{ELBO}$ 就是重构误差 + KL散度。

5. 总结

负对数似然的变分下界（ELBO）是一个可优化的目标函数，通过引入简单的分布 $q_{\varphi }(z|x)$ 来近似复杂后验，从而解决隐变量模型的学习问题。其核心思想是用可计算的ELBO代替不可计算的对数似然，并通过优化ELBO平衡数据拟合（重构）和模型复杂度（KL正则）。

---

参考

• 狗都能看懂的DDPM论文
• DDPM论文解读1
• DDPM论文解读2