机器学习算法全景解析：从理论到实践

机器学习算法全景解析：从理论到实践

引言

机器学习作为人工智能的核心组成部分，正在深刻地改变我们的世界。从推荐系统到自动驾驶，从医疗诊断到金融风控，机器学习算法无处不在。本文将全面系统地介绍机器学习的主要算法类别及其核心知识点，帮助读者构建完整的机器学习知识体系。

一、机器学习基础概念

1.1 机器学习定义

机器学习是一门研究如何通过数据自动改进计算机程序性能的学科。其核心思想是：通过算法解析数据，从中学习规律，然后对真实世界中的事件做出决策或预测。

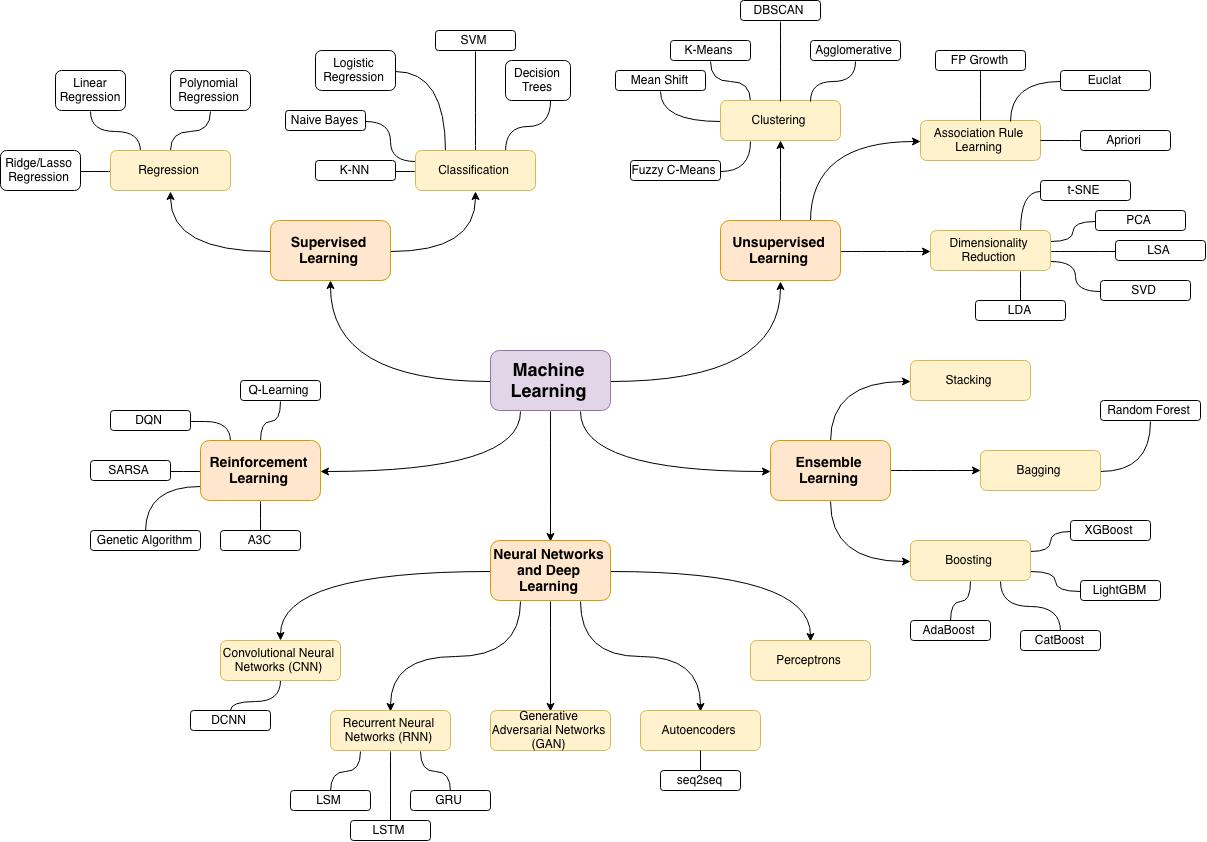
1.2 机器学习分类

• 监督学习：使用带有标签的数据训练模型

• 无监督学习：使用无标签的数据发现内在模式

• 半监督学习：结合少量标注数据和大量未标注数据

• 强化学习：通过与环境交互学习最优策略

1.3 基本术语

• 特征（Feature）：输入变量

• 标签（Label）：输出变量（监督学习）

• 样本（Sample）：单个数据点

• 数据集（Dataset）：样本集合

• 训练（Training）：模型学习过程

• 推理（Inference）：模型预测过程

二、监督学习算法

2.1 线性回归

核心思想：建立特征与连续目标值之间的线性关系

数学模型：
$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n + \epsilon$

损失函数：均方误差（MSE）
$MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2$

优化方法：

• 最小二乘法（解析解）

• 梯度下降（数值解）

正则化变体：

• 岭回归（L2正则化）

• Lasso回归（L1正则化）

• ElasticNet（L1+L2正则化）

2.2 逻辑回归

核心思想：解决二分类问题，输出概率值

数学模型：
$P(y=1|x) = \frac{1}{1 + e^{-(\beta_0 + \beta^Tx)}}$

损失函数：交叉熵损失
$J(\theta) = -\frac{1}{n}\sum_{i=1}^{n}[y_i\log(\hat{y_i}) + (1-y_i)\log(1-\hat{y_i})]$

多分类扩展：

• One-vs-Rest (OvR)

• Softmax回归（多类逻辑回归）

2.3 支持向量机（SVM）

核心思想：寻找最大间隔超平面分离数据

线性可分情况：
$\min_{w,b} \frac{1}{2}||w||^2$ s.t. $y_i(w^Tx_i + b) \geq 1$

非线性扩展：

• 核技巧：将数据映射到高维空间

• 常用核函数：多项式核、高斯核（RBF）、Sigmoid核

软间隔SVM：处理噪声和不可分数据
$\min_{w,b,\xi} \frac{1}{2}||w||^2 + C\sum_{i=1}^{n}\xi_i$

2.4 决策树

核心思想：基于特征对数据递归划分

分裂标准：

• 信息增益（ID3算法）

• 信息增益比（C4.5算法）

• 基尼指数（CART算法）

剪枝策略：

• 预剪枝：提前终止树生长

• 后剪枝：生成完整树后剪枝

优缺点：

• 优点：可解释性强、无需特征缩放、处理混合类型数据

• 缺点：容易过拟合、对数据微小变化敏感

2.5 随机森林

核心思想：集成多棵决策树，通过投票提高性能

关键机制：

• Bagging：自助采样构建多个训练集

• 特征随机性：每个节点分裂时随机选择特征子集

超参数：

• 树的数量（n_estimators）

• 最大深度（max_depth）

• 最小分裂样本数（min_samples_split）

2.6 梯度提升机

核心思想：逐步添加弱学习器，纠正前一个模型的错误

常见实现：

• XGBoost：添加正则化项，防止过拟合

• LightGBM：基于直方图的优化，训练速度快

• CatBoost：专门处理类别特征

核心公式：
$F_m(x) = F_{m-1}(x) + \gamma_m h_m(x)$

三、无监督学习算法

3.1 K均值聚类

核心思想：将数据划分为K个簇，使簇内方差最小

算法步骤：

1. 随机选择K个初始质心

2. 将每个点分配到最近的质心

3. 重新计算质心位置

4. 重复2-3步直到收敛

局限性：

• 需要预先指定K值

• 对初始质心敏感

• 只能发现球形簇

3.2 层次聚类

核心思想：通过层次分解或合并构建聚类树

两种策略：

• 凝聚式（自底向上）：初始每个样本为一类，逐步合并

• 分裂式（自顶向下）：初始所有样本为一类，逐步分裂

距离度量：

• 单链接：最小簇间距离

• 全链接：最大簇间距离

• 平均链接：平均簇间距离

3.3 主成分分析（PCA）

核心思想：通过正交变换将相关变量转为不相关的主成分

数学原理：

• 计算协方差矩阵

• 特征值分解

• 选择前k大特征值对应的特征向量

应用场景：

• 数据降维

• 数据可视化

• 噪声过滤

3.4 异常检测算法

隔离森林：通过随机分割隔离异常点
One-Class SVM：学习正常数据的边界
自编码器：通过重建误差检测异常

四、神经网络与深度学习

4.1 感知机与多层感知机

单层感知机：最简单的神经网络结构
$y = f(\sum_{i=1}^{n}w_ix_i + b)$

激活函数：

• Sigmoid：$\sigma(x) = \frac{1}{1 + e^{-x}}$

• Tanh：$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

• ReLU：$f(x) = \max(0, x)$

反向传播算法：通过链式法则计算梯度

4.2 卷积神经网络（CNN）

核心结构：

• 卷积层：提取局部特征

• 池化层：降维，保持平移不变性

• 全连接层：整合特征进行分类

经典架构：

• LeNet-5：早期成功应用于手写数字识别

• AlexNet：深度学习复兴的标志

• ResNet：残差连接解决梯度消失

4.3 循环神经网络（RNN）

核心思想：处理序列数据，具有记忆功能

变体结构：

• LSTM：门控机制解决长程依赖

• GRU：简化版LSTM，计算效率更高

应用领域：

• 自然语言处理

• 时间序列预测

• 语音识别

4.4 Transformer与自注意力机制

自注意力机制：计算输入序列中每个位置与其他位置的相关性

Transformer架构：

• 编码器-解码器结构

• 多头注意力机制

• 位置编码

衍生模型：

• BERT：双向编码器表示

• GPT：生成式预训练变换器

五、模型评估与优化

5.1 评估指标

分类问题：

• 准确率、精确率、召回率、F1分数

• ROC曲线与AUC值

• 混淆矩阵

回归问题：

• 均方误差（MSE）

• 平均绝对误差（MAE）

• R平方系数

5.2 偏差-方差权衡

偏差：模型预测值与真实值的差异
方差：模型对训练数据变化的敏感性
权衡策略：通过正则化、集成学习等方法平衡

5.3 交叉验证

k折交叉验证：将数据分为k份，轮流使用k-1份训练，1份测试
留一法交叉验证：k等于样本数
分层交叉验证：保持每折中类别比例相同

5.4 超参数调优

网格搜索：遍历所有参数组合
随机搜索：随机采样参数空间
贝叶斯优化：基于先前评估结果选择下一个参数

六、实际应用考虑

6.1 特征工程

特征缩放：标准化、归一化
特征编码：独热编码、标签编码
特征选择：过滤法、包装法、嵌入法
特征提取：PCA、LDA、t-SNE

6.2 类别不平衡处理

采样方法：

• 过采样（如SMOTE）

• 欠采样

算法层面：

• 类别权重调整

• 代价敏感学习

6.3 模型部署与监控

部署方式：批量预测、实时推理
监控指标：预测准确性、响应延迟、资源使用率
模型更新：全量更新、增量更新、在线学习

七、总结与展望

机器学习算法种类繁多，各有其适用场景和优缺点。在实际应用中，需要根据具体问题和数据特点选择合适的算法。未来机器学习的发展趋势包括：

1. 自动化机器学习：减少人工干预

2. 可解释AI：增强模型透明度

3. 联邦学习：保护数据隐私

4. 强化学习应用扩展：解决更复杂决策问题

掌握机器学习算法不仅需要理解数学原理，还需要通过实践积累经验。希望本文能为您的机器学习学习之旅提供有价值的参考。

---

进一步学习资源：

• 《机器学习》周志华

• 《Pattern Recognition and Machine Learning》Bishop

• Coursera: Machine Learning by Andrew Ng

• Kaggle竞赛：实践平台

注：本文仅概述了机器学习算法的主要知识点，每个算法都值得深入研究和实践。建议读者结合实际项目，深化对各类算法的理解。

写一篇关于机器学习各个算法的知识点的博客，要求内容详细，附有代码实例，不少于10000字

机器学习算法全景解析：从理论到实践

引言

机器学习作为人工智能的核心组成部分，正在深刻地改变我们的世界。从推荐系统到自动驾驶，从医疗诊断到金融风控，机器学习算法无处不在。本文将全面系统地介绍机器学习的主要算法类别及其核心知识点，通过详细的数学解释和完整的代码示例，帮助读者构建完整的机器学习知识体系。

一、机器学习基础概念

1.1 机器学习定义

机器学习是一门研究如何通过数据自动改进计算机程序性能的学科。其核心思想是：通过算法解析数据，从中学习规律，然后对真实世界中的事件做出决策或预测。

1.2 机器学习分类

• 监督学习：使用带有标签的数据训练模型，包括分类和回归问题

• 无监督学习：使用无标签的数据发现内在模式，包括聚类和降维

• 半监督学习：结合少量标注数据和大量未标注数据进行学习

• 强化学习：通过与环境交互学习最优策略，获得最大累积奖励

1.3 基本术语详解

• 特征（Feature）：描述数据的输入变量，可以是数值型、类别型等

• 标签（Label）：在监督学习中的输出变量，是我们要预测的目标

• 样本（Sample）：单个数据实例，包含一组特征和可能的标签

• 数据集（Dataset）：样本的集合，通常分为训练集、验证集和测试集

• 训练（Training）：模型从数据中学习规律的过程

• 推理（Inference）：使用训练好的模型对新数据进行预测

1.4 开发环境设置

在开始代码实践前，我们先设置开发环境：

python

# 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import accuracy_score, mean_squared_error, classification_report
from sklearn.preprocessing import StandardScaler, LabelEncoder# 设置随机种子保证结果可重现
np.random.seed(42)# 设置绘图风格
plt.style.use('seaborn-v0_8-whitegrid')
sns.set_palette("husl")# 忽略警告信息
import warnings
warnings.filterwarnings('ignore')print("环境设置完成！所有必要库已导入。")

二、监督学习算法详解

2.1 线性回归

2.1.1 核心理论与数学原理

线性回归是机器学习中最基础的算法之一，用于建立特征与连续目标值之间的线性关系。

数学模型：
对于有n个特征的样本，线性回归模型表示为：
$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n + \epsilon$

其中：

• $y$ 是目标变量

• $\beta_0$ 是截距项

• $\beta_1, \beta_2, ..., \beta_n$ 是系数

• $x_1, x_2, ..., x_n$ 是特征变量

• $\epsilon$ 是误差项

损失函数：均方误差（MSE）
$MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2$

优化方法：

1. 最小二乘法：通过解析解直接计算最优参数
   $\beta = (X^TX)^{-1}X^Ty$

2. 梯度下降：通过迭代方式逐步优化参数
   $\beta_j = \beta_j - \alpha \frac{\partial}{\partial \beta_j}J(\beta)$

2.1.2 代码实现与示例

python

class LinearRegression:def __init__(self, learning_rate=0.01, n_iterations=1000):self.learning_rate = learning_rateself.n_iterations = n_iterationsself.weights = Noneself.bias = Noneself.loss_history = []def fit(self, X, y):# 初始化参数n_samples, n_features = X.shapeself.weights = np.zeros(n_features)self.bias = 0# 梯度下降for i in range(self.n_iterations):# 预测y_pred = np.dot(X, self.weights) + self.bias# 计算梯度dw = (1/n_samples) * np.dot(X.T, (y_pred - y))db = (1/n_samples) * np.sum(y_pred - y)# 更新参数self.weights -= self.learning_rate * dwself.bias -= self.learning_rate * db# 记录损失loss = np.mean((y_pred - y)**2)self.loss_history.append(loss)if i % 100 == 0:print(f"Iteration {i}, Loss: {loss:.4f}")def predict(self, X):return np.dot(X, self.weights) + self.bias# 生成示例数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 数据可视化
plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plt.scatter(X, y, alpha=0.7)
plt.xlabel('X')
plt.ylabel('y')
plt.title('原始数据分布')# 训练模型
model = LinearRegression(learning_rate=0.1, n_iterations=1000)
model.fit(X, y)# 预测
X_test = np.linspace(0, 2, 100).reshape(-1, 1)
y_pred = model.predict(X_test)plt.subplot(1, 2, 2)
plt.scatter(X, y, alpha=0.7, label='真实数据')
plt.plot(X_test, y_pred, 'r-', label='预测结果', linewidth=2)
plt.xlabel('X')
plt.ylabel('y')
plt.title('线性回归拟合结果')
plt.legend()plt.tight_layout()
plt.show()# 损失曲线
plt.figure(figsize=(10, 4))
plt.plot(model.loss_history)
plt.xlabel('迭代次数')
plt.ylabel('损失值')
plt.title('梯度下降损失曲线')
plt.show()print(f"最终权重: {model.weights[0]:.4f}, 偏置: {model.bias:.4f}")

2.1.3 正则化变体

岭回归（L2正则化）：
$J(\beta) = \sum_{i=1}^{n}(y_i - \hat{y_i})^2 + \lambda\sum_{j=1}^{p}\beta_j^2$

Lasso回归（L1正则化）：
$J(\beta) = \sum_{i=1}^{n}(y_i - \hat{y_i})^2 + \lambda\sum_{j=1}^{p}|\beta_j|$

ElasticNet（L1+L2正则化）：
$J(\beta) = \sum_{i=1}^{n}(y_i - \hat{y_i})^2 + \lambda_1\sum_{j=1}^{p}|\beta_j| + \lambda_2\sum_{j=1}^{p}\beta_j^2$

python

from sklearn.linear_model import Ridge, Lasso, ElasticNet
from sklearn.model_selection import GridSearchCV# 创建更复杂的数据
np.random.seed(42)
X = 6 * np.random.rand(100, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(100, 1)# 添加多项式特征
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)# 比较不同正则化方法
models = {'Linear': LinearRegression(),'Ridge': Ridge(alpha=0.1),'Lasso': Lasso(alpha=0.1),'ElasticNet': ElasticNet(alpha=0.1, l1_ratio=0.5)
}plt.figure(figsize=(15, 10))for i, (name, model) in enumerate(models.items(), 1):model.fit(X_poly, y)X_test = np.linspace(-3, 3, 100).reshape(-1, 1)X_test_poly = poly.transform(X_test)y_pred = model.predict(X_test_poly)plt.subplot(2, 2, i)plt.scatter(X, y, alpha=0.7)plt.plot(X_test, y_pred, 'r-', linewidth=2)plt.title(f'{name} Regression')plt.xlabel('X')plt.ylabel('y')plt.tight_layout()
plt.show()

2.2 逻辑回归

2.2.1 核心理论与数学原理

逻辑回归虽然名字中有"回归"，但实际上是解决二分类问题的算法。它通过Sigmoid函数将线性回归的输出映射到(0,1)区间，表示概率。

Sigmoid函数：
$\sigma(z) = \frac{1}{1 + e^{-z}}$

其中 $z = \beta_0 + \beta_1x_1 + ... + \beta_nx_n$

决策边界：当 $\sigma(z) \geq 0.5$ 时预测为正类，否则为负类

损失函数：交叉熵损失
$J(\theta) = -\frac{1}{n}\sum_{i=1}^{n}[y_i\log(\hat{y_i}) + (1-y_i)\log(1-\hat{y_i})]$

梯度计算：
$\frac{\partial J}{\partial \beta_j} = \frac{1}{n}\sum_{i=1}^{n}(\hat{y_i} - y_i)x_{ij}$

2.2.2 代码实现与示例

python

class LogisticRegression:def __init__(self, learning_rate=0.01, n_iterations=1000):self.learning_rate = learning_rateself.n_iterations = n_iterationsself.weights = Noneself.bias = Noneself.loss_history = []def _sigmoid(self, z):# 防止溢出z = np.clip(z, -500, 500)return 1 / (1 + np.exp(-z))def fit(self, X, y):n_samples, n_features = X.shapeself.weights = np.zeros(n_features)self.bias = 0for i in range(self.n_iterations):# 计算线性组合linear_model = np.dot(X, self.weights) + self.biasy_pred = self._sigmoid(linear_model)# 计算梯度dw = (1/n_samples) * np.dot(X.T, (y_pred - y))db = (1/n_samples) * np.sum(y_pred - y)# 更新参数self.weights -= self.learning_rate * dwself.bias -= self.learning_rate * db# 计算损失loss = -np.mean(y * np.log(y_pred + 1e-15) + (1 - y) * np.log(1 - y_pred + 1e-15))self.loss_history.append(loss)if i % 100 == 0:print(f"Iteration {i}, Loss: {loss:.4f}")def predict_proba(self, X):linear_model = np.dot(X, self.weights) + self.biasreturn self._sigmoid(linear_model)def predict(self, X, threshold=0.5):return (self.predict_proba(X) >= threshold).astype(int)# 生成分类数据
from sklearn.datasets import make_classificationX, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0,n_clusters_per_class=1,random_state=42
)# 数据可视化
plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', alpha=0.7)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('分类数据分布')
plt.colorbar()# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 特征标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 训练逻辑回归模型
model = LogisticRegression(learning_rate=0.1, n_iterations=2000)
model.fit(X_train_scaled, y_train)# 预测
y_pred = model.predict(X_test_scaled)
accuracy = accuracy_score(y_test, y_pred)
print(f"测试集准确率: {accuracy:.4f}")# 绘制决策边界
def plot_decision_boundary(model, X, y):x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.3, cmap='coolwarm')plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', alpha=0.7)plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.title('逻辑回归决策边界')plt.subplot(1, 2, 2)
plot_decision_boundary(model, X_test_scaled, y_test)
plt.tight_layout()
plt.show()# 损失曲线
plt.figure(figsize=(10, 4))
plt.plot(model.loss_history)
plt.xlabel('迭代次数')
plt.ylabel('损失值')
plt.title('逻辑回归训练损失曲线')
plt.show()

2.2.3 多分类扩展

python

# 多分类逻辑回归示例
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression as SKLogisticRegression# 生成多分类数据
X_multi, y_multi = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0,n_classes=3,n_clusters_per_class=1,random_state=42
)# 使用scikit-learn的多分类逻辑回归
multi_model = SKLogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=1000)
multi_model.fit(X_multi, y_multi)# 绘制决策边界
plt.figure(figsize=(12, 5))def plot_multi_decision_boundary(model, X, y):x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.3, cmap='viridis')plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', alpha=0.7)plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.title('多分类逻辑回归决策边界')plot_multi_decision_boundary(multi_model, X_multi, y_multi)
plt.colorbar(ticks=range(3))
plt.show()# 评估多分类性能
y_multi_pred = multi_model.predict(X_multi)
print("多分类报告:")
print(classification_report(y_multi, y_multi_pred))

2.3 支持向量机（SVM）

2.3.1 核心理论与数学原理

支持向量机是一种强大的分类算法，其核心思想是寻找一个最优超平面来分离不同类别的数据，同时最大化边界（margin）。

线性可分SVM：
对于线性可分数据，SVM寻找一个超平面：
$w^Tx + b = 0$

满足约束条件：
$y_i(w^Tx_i + b) \geq 1, \quad \forall i$

优化目标：
$\min_{w,b} \frac{1}{2}||w||^2$

软间隔SVM：
对于非线性可分数据，引入松弛变量ξ：
$\min_{w,b,\xi} \frac{1}{2}||w||^2 + C\sum_{i=1}^{n}\xi_i$
约束条件：
$y_i(w^Tx_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0$

核技巧：
通过核函数将数据映射到高维空间：
$K(x_i, x_j) = \phi(x_i)^T\phi(x_j)$

常用核函数：

• 线性核：$K(x_i, x_j) = x_i^Tx_j$

• 多项式核：$K(x_i, x_j) = (\gamma x_i^Tx_j + r)^d$

• 高斯核（RBF）：$K(x_i, x_j) = \exp(-\gamma||x_i - x_j||^2)$

2.3.2 代码实现与示例

python

class SVM:def __init__(self, learning_rate=0.001, lambda_param=0.01, n_iterations=1000):self.lr = learning_rateself.lambda_param = lambda_paramself.n_iters = n_iterationsself.w = Noneself.b = Nonedef fit(self, X, y):n_samples, n_features = X.shape# 将y标签转换为1和-1y_ = np.where(y <= 0, -1, 1)# 初始化参数self.w = np.zeros(n_features)self.b = 0# 梯度下降for _ in range(self.n_iters):for idx, x_i in enumerate(X):condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1if condition:self.w -= self.lr * (2 * self.lambda_param * self.w)else:self.w -= self.lr * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))self.b -= self.lr * y_[idx]def predict(self, X):linear_output = np.dot(X, self.w) - self.breturn np.sign(linear_output)# 生成线性可分数据
from sklearn.datasets import make_blobsX, y = make_blobs(n_samples=100, centers=2, random_state=42, cluster_std=0.6)
y = np.where(y == 0, -1, 1)  # 转换为-1和1# 训练SVM
svm_model = SVM(learning_rate=0.001, lambda_param=0.01, n_iterations=1000)
svm_model.fit(X, y)# 可视化结果
def plot_svm_decision_boundary(model, X, y):w = model.wb = model.bx_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.3, cmap='coolwarm')plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', alpha=0.7)# 绘制支持向量和决策边界x_hyperplane = np.linspace(x_min, x_max, 100)y_hyperplane = (w[0] * x_hyperplane - b) / w[1]margin = 1 / np.sqrt(np.sum(w**2))plt.plot(x_hyperplane, y_hyperplane, 'k-', label='决策边界')plt.plot(x_hyperplane, y_hyperplane - margin/w[1], 'k--', label='边界')plt.plot(x_hyperplane, y_hyperplane + margin/w[1], 'k--')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.legend()plt.title('SVM决策边界和支持向量')plt.figure(figsize=(10, 6))
plot_svm_decision_boundary(svm_model, X, y)
plt.show()# 使用scikit-learn的SVM处理非线性数据
from sklearn.svm import SVC
from sklearn.datasets import make_circles# 生成非线性数据
X_nonlinear, y_nonlinear = make_circles(n_samples=100, factor=0.3, noise=0.1, random_state=42)# 使用RBF核的SVM
svm_rbf = SVC(kernel='rbf', C=1.0, gamma='scale')
svm_rbf.fit(X_nonlinear, y_nonlinear)# 可视化非线性SVM
def plot_nonlinear_svm(model, X, y):x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.3, cmap='coolwarm')plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', alpha=0.7)plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.title('非线性SVM（RBF核）')plt.figure(figsize=(10, 6))
plot_nonlinear_svm(svm_rbf, X_nonlinear, y_nonlinear)
plt.show()# 比较不同核函数
kernels = ['linear', 'poly', 'rbf', 'sigmoid']plt.figure(figsize=(15, 10))for i, kernel in enumerate(kernels, 1):model = SVC(kernel=kernel, gamma='scale', degree=3)model.fit(X_nonlinear, y_nonlinear)plt.subplot(2, 2, i)plot_nonlinear_svm(model, X_nonlinear, y_nonlinear)plt.title(f'SVM with {kernel} kernel')plt.tight_layout()
plt.show()

2.4 决策树

2.4.1 核心理论与数学原理

决策树是一种基于树结构的分类和回归算法，通过一系列的判断规则对数据进行划分。

关键概念：

1. 节点：包含根节点、内部节点、叶节点

2. 分裂标准：选择最佳特征和分割点

3. 停止条件：最大深度、最小样本数等

分裂标准：

1. 信息增益（ID3算法）：
   $IG(D_p, f) = I(D_p) - \sum_{j=1}^{m}\frac{N_j}{N_p}I(D_j)$
   其中 $I$ 是基尼不纯度或熵

2. 基尼指数（CART算法）：
   $Gini(D) = 1 - \sum_{i=1}^{k}p_i^2$

3. 信息增益比（C4.5算法）：
   $GainRatio(f) = \frac{IG(f)}{IV(f)}$
   其中 $IV(f)$ 是特征f的固有值

剪枝策略：

• 预剪枝：在生长过程中提前停止

• 后剪枝：生成完整树后进行剪枝

2.4.2 代码实现与示例

python

class DecisionTree:def __init__(self, max_depth=None, min_samples_split=2, criterion='gini'):self.max_depth = max_depthself.min_samples_split = min_samples_splitself.criterion = criterionself.tree = Nonedef _gini(self, y):classes = np.unique(y)gini = 0for cls in classes:p = np.sum(y == cls) / len(y)gini += p * (1 - p)return ginidef _entropy(self, y):classes = np.unique(y)entropy = 0for cls in classes:p = np.sum(y == cls) / len(y)if p > 0:entropy -= p * np.log2(p)return entropydef _information_gain(self, parent, left_child, right_child, criterion):if criterion == 'gini':impurity_func = self._ginielse:  # entropyimpurity_func = self._entropyparent_impurity = impurity_func(parent)n = len(parent)n_l, n_r = len(left_child), len(right_child)if n_l == 0 or n_r == 0:return 0child_impurity = (n_l / n) * impurity_func(left_child) + (n_r / n) * impurity_func(right_child)return parent_impurity - child_impuritydef _best_split(self, X, y):best_gain = 0best_feature = Nonebest_threshold = Nonen_features = X.shape[1]for feature_idx in range(n_features):feature_values = X[:, feature_idx]unique_values = np.unique(feature_values)for threshold in unique_values:left_indices = feature_values <= thresholdright_indices = feature_values > thresholdif np.sum(left_indices) == 0 or np.sum(right_indices) == 0:continueleft_y = y[left_indices]right_y = y[right_indices]gain = self._information_gain(y, left_y, right_y, self.criterion)if gain > best_gain:best_gain = gainbest_feature = feature_idxbest_threshold = thresholdreturn best_feature, best_threshold, best_gaindef _build_tree(self, X, y, depth=0):n_samples, n_features = X.shapen_classes = len(np.unique(y))# 停止条件if (self.max_depth is not None and depth >= self.max_depth orn_samples < self.min_samples_split orn_classes == 1):return {'class': np.bincount(y).argmax(), 'is_leaf': True}# 寻找最佳分裂feature, threshold, gain = self._best_split(X, y)if gain == 0:  # 无法继续分裂return {'class': np.bincount(y).argmax(), 'is_leaf': True}# 递归构建子树left_indices = X[:, feature] <= thresholdright_indices = X[:, feature] > thresholdleft_subtree = self._build_tree(X[left_indices], y[left_indices], depth + 1)right_subtree = self._build_tree(X[right_indices], y[right_indices], depth + 1)return {'feature': feature,'threshold': threshold,'left': left_subtree,'right': right_subtree,'is_leaf': False}def fit(self, X, y):self.tree = self._build_tree(X, y)def _predict_sample(self, x, tree):if tree['is_leaf']:return tree['class']if x[tree['feature']] <= tree['threshold']:return self._predict_sample(x, tree['left'])else:return self._predict_sample(x, tree['right'])def predict(self, X):return np.array([self._predict_sample(x, self.tree) for x in X])# 使用决策树进行分类
from sklearn.datasets import load_irisiris = load_iris()
X_iris, y_iris = iris.data, iris.target# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X_iris, y_iris, test_size=0.2, random_state=42)# 训练自定义决策树
dt_model = DecisionTree(max_depth=3, criterion='gini')
dt_model.fit(X_train, y_train)# 预测
y_pred = dt_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"自定义决策树准确率: {accuracy:.4f}")# 与scikit-learn决策树比较
from sklearn.tree import DecisionTreeClassifier, plot_treesk_dt = DecisionTreeClassifier(max_depth=3, random_state=42)
sk_dt.fit(X_train, y_train)
sk_accuracy = accuracy_score(y_test, sk_dt.predict(X_test))
print(f"Scikit-learn决策树准确率: {sk_accuracy:.4f}")# 可视化决策树
plt.figure(figsize=(15, 10))
plot_tree(sk_dt, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.title('决策树结构可视化')
plt.show()# 决策边界可视化（选择两个特征）
X_2d = X_iris[:, :2]  # 只使用前两个特征
y_2d = y_irisX_train_2d, X_test_2d, y_train_2d, y_test_2d = train_test_split(X_2d, y_2d, test_size=0.2, random_state=42)dt_2d = DecisionTreeClassifier(max_depth=3, random_state=42)
dt_2d.fit(X_train_2d, y_train_2d)def plot_decision_tree_boundary(model, X, y):x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.3, cmap='viridis')plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', alpha=0.7)plt.xlabel(iris.feature_names[0])plt.ylabel(iris.feature_names[1])plt.title('决策树决策边界')plt.figure(figsize=(10, 6))
plot_decision_tree_boundary(dt_2d, X_test_2d, y_test_2d)
plt.show()

2.5 随机森林

2.5.1 核心理论与数学原理

随机森林是一种集成学习方法，通过构建多棵决策树并综合它们的预测结果来提高模型性能。

核心思想：

1. Bootstrap Aggregating (Bagging)：从原始数据集中有放回地随机抽取样本，构建多个训练子集

2. 特征随机性：在每个节点分裂时，随机选择特征子集进行考虑

3. 投票机制：多棵树通过投票或平均得出最终预测

数学原理：
对于分类问题：
$\hat{y} = \text{mode}{h_1(x), h_2(x), ..., h_T(x)}$

对于回归问题：
$\hat{y} = \frac{1}{T}\sum_{i=1}^{T}h_i(x)$

优点：

• 减少过拟合

• 处理高维数据

• 提供特征重要性评估

• 对缺失值不敏感

2.5.2 代码实现与示例

python

class RandomForest:def __init__(self, n_estimators=100, max_depth=None, min_samples_split=2,max_features='auto', random_state=None):self.n_estimators = n_estimatorsself.max_depth = max_depthself.min_samples_split = min_samples_splitself.max_features = max_featuresself.random_state = random_stateself.trees = []self.feature_importances_ = Noneif random_state is not None:np.random.seed(random_state)def _bootstrap_sample(self, X, y):n_samples = X.shape[0]indices = np.random.choice(n_samples, n_samples, replace=True)return X[indices], y[indices]def _get_max_features(self, n_features):if self.max_features == 'auto':return int(np.sqrt(n_features))elif self.max_features == 'sqrt':return int(np.sqrt(n_features))elif self.max_features == 'log2':return int(np.log2(n_features))else:return self.max_featuresdef fit(self, X, y):n_samples, n_features = X.shapeself.trees = []feature_importances = np.zeros(n_features)max_features = self._get_max_features(n_features)for i in range(self.n_estimators):# Bootstrap采样X_boot, y_boot = self._bootstrap_sample(X, y)# 创建决策树tree = DecisionTreeClassifier(max_depth=self.max_depth,min_samples_split=self.min_samples_split,max_features=max_features,random_state=self.random_state + i if self.random_state is not None else None)# 训练决策树tree.fit(X_boot, y_boot)self.trees.append(tree)# 累计特征重要性if hasattr(tree, 'feature_importances_'):feature_importances += tree.feature_importances_# 计算平均特征重要性self.feature_importances_ = feature_importances / self.n_estimatorsdef predict(self, X):# 收集所有树的预测tree_preds = np.array([tree.predict(X) for tree in self.trees])# 多数投票if tree_preds.ndim == 2:  # 分类问题return np.apply_along_axis(lambda x: np.bincount(x).argmax(), axis=0, arr=tree_preds)else:  # 回归问题return np.mean(tree_preds, axis=0)def predict_proba(self, X):# 收集所有树的概率预测tree_probas = np.array([tree.predict_proba(X) for tree in self.trees])# 平均概率return np.mean(tree_probas, axis=0)# 使用随机森林
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification# 生成复杂数据
X_complex, y_complex = make_classification(n_samples=1000,n_features=20,n_informative=15,n_redundant=5,n_classes=3,random_state=42
)# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X_complex, y_complex, test_size=0.2, random_state=42)# 训练随机森林
rf_model = RandomForestClassifier(n_estimators=100,max_depth=10,random_state=42
)
rf_model.fit(X_train, y_train)# 预测
y_pred = rf_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"随机森林准确率: {accuracy:.4f}")# 特征重要性可视化
plt.figure(figsize=(12, 6))
feature_importance = rf_model.feature_importances_
sorted_idx = np.argsort(feature_importance)plt.barh(range(len(sorted_idx)), feature_importance[sorted_idx])
plt.yticks(range(len(sorted_idx)), [f'Feature {i}' for i in sorted_idx])
plt.xlabel('特征重要性')
plt.title('随机森林特征重要性')
plt.tight_layout()
plt.show()# 比较不同数量的树对性能的影响
n_trees_range = [1, 5, 10, 20, 50, 100, 200]
accuracies = []for n_trees in n_trees_range:model = RandomForestClassifier(n_estimators=n_trees, random_state=42)model.fit(X_train, y_train)y_pred = model.predict(X_test)accuracies.append(accuracy_score(y_test, y_pred))plt.figure(figsize=(10, 6))
plt.plot(n_trees_range, accuracies, 'o-')
plt.xlabel('树的数量')
plt.ylabel('准确率')
plt.title('随机森林性能随树数量变化')
plt.xscale('log')
plt.grid(True, alpha=0.3)
plt.show()# 比较随机森林和单棵决策树
dt_single = DecisionTreeClassifier(max_depth=10, random_state=42)
dt_single.fit(X_train, y_train)
dt_accuracy = accuracy_score(y_test, dt_single.predict(X_test))print(f"单棵决策树准确率: {dt_accuracy:.4f}")
print(f"随机森林准确率: {accuracy:.4f}")
print(f"性能提升: {(accuracy - dt_accuracy):.4f}")# 超参数调优
from sklearn.model_selection import GridSearchCVparam_grid = {'n_estimators': [50, 100, 200],'max_depth': [None, 10, 20],'min_samples_split': [2, 5, 10],'max_features': ['auto', 'sqrt', 'log2']
}rf = RandomForestClassifier(random_state=42)
grid_search = GridSearchCV(rf, param_grid, cv=5, scoring='accuracy', n_jobs=-1)
grid_search.fit(X_train, y_train)print("最佳参数:", grid_search.best_params_)
print("最佳交叉验证分数:", grid_search.best_score_)# 使用最佳参数训练最终模型
best_rf = grid_search.best_estimator_
final_accuracy = accuracy_score(y_test, best_rf.predict(X_test))
print(f"调优后随机森林准确率: {final_accuracy:.4f}")

2.6 梯度提升机

2.6.1 核心理论与数学原理

梯度提升是一种强大的集成学习技术，通过逐步添加弱学习器来纠正前一个模型的错误。

核心思想：

1. 加法模型：$F_m(x) = F_{m-1}(x) + \gamma_m h_m(x)$

2. 梯度下降：在函数空间中进行梯度下降

3. 损失函数优化：最小化特定损失函数

算法步骤：

1. 初始化模型：$F_0(x) = \arg\min_{\gamma}\sum_{i=1}^{n}L(y_i, \gamma)$

2. 对于m=1到M：
   a. 计算伪残差：$r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]{F(x)=F{m-1}(x)}$
   b. 用基学习器拟合伪残差：$h_m(x)$
   c. 计算步长：$\gamma_m = \arg\min_{\gamma}\sum_{i=1}^{n}L(y_i, F_{m-1}(x_i) + \gamma h_m(x_i))$
   d. 更新模型：$F_m(x) = F_{m-1}(x) + \gamma_m h_m(x_i)$

常见实现：

• XGBoost：添加正则化项，防止过拟合

• LightGBM：基于直方图的优化，训练速度快

• CatBoost：专门处理类别特征

2.6.2 代码实现与示例

python

class GradientBoosting:def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=None):self.n_estimators = n_estimatorsself.learning_rate = learning_rateself.max_depth = max_depthself.random_state = random_stateself.trees = []self.initial_prediction = Noneif random_state is not None:np.random.seed(random_state)def _mean_squared_error_gradient(self, y, y_pred):return y - y_preddef fit(self, X, y):# 初始预测（平均值）self.initial_prediction = np.mean(y)current_prediction = np.full_like(y, self.initial_prediction, dtype=float)self.trees = []for i in range(self.n_estimators):# 计算伪残差（负梯度）residuals = self._mean_squared_error_gradient(y, current_prediction)# 用决策树拟合残差tree = DecisionTreeRegressor(max_depth=self.max_depth, random_state=self.random_state)tree.fit(X, residuals)# 更新预测tree_pred = tree.predict(X)current_prediction += self.learning_rate * tree_pred# 保存树self.trees.append(tree)def predict(self, X):# 初始预测y_pred = np.full(X.shape[0], self.initial_prediction, dtype=float)# 累加所有树的预测for tree in self.trees:y_pred += self.learning_rate * tree.predict(X)return y_pred# 使用梯度提升进行回归
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.datasets import make_regression# 生成回归数据
X_reg, y_reg = make_regression(n_samples=1000,n_features=10,n_informative=8,noise=0.1,random_state=42
)# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X_reg, y_reg, test_size=0.2, random_state=42)# 训练梯度提升模型
gb_model = GradientBoostingRegressor(n_estimators=100,learning_rate=0.1,max_depth=3,random_state=42
)
gb_model.fit(X_train, y_train)# 预测
y_pred = gb_model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"梯度提升MSE: {mse:.4f}")# 学习曲线
train_errors = []
test_errors = []for n_est in range(1, 201, 10):model = GradientBoostingRegressor(n_estimators=n_est,learning_rate=0.1,max_depth=3,random_state=42)model.fit(X_train, y_train)train_pred = model.predict(X_train)test_pred = model.predict(X_test)train_errors.append(mean_squared_error(y_train, train_pred))test_errors.append(mean_squared_error(y_test, test_pred))plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plt.plot(range(1, 201, 10), train_errors, label='训练误差')
plt.plot(range(1, 201, 10), test_errors, label='测试误差')
plt.xlabel('树的数量')
plt.ylabel('MSE')
plt.title('梯度提升学习曲线')
plt.legend()plt.subplot(1, 2, 2)
plt.plot(range(1, 201, 10), test_errors)
plt.xlabel('树的数量')
plt.ylabel('测试MSE')
plt.title('测试误差随树数量变化')
plt.tight_layout()
plt.show()# 特征重要性
plt.figure(figsize=(10, 6))
feature_importance = gb_model.feature_importances_
sorted_idx = np.argsort(feature_importance)plt.barh(range(len(sorted_idx)), feature_importance[sorted_idx])
plt.yticks(range(len(sorted_idx)), [f'Feature {i}' for i in sorted_idx])
plt.xlabel('特征重要性')
plt.title('梯度提升特征重要性')
plt.tight_layout()
plt.show()# 比较不同学习率
learning_rates = [0.01, 0.05, 0.1, 0.2, 0.5]
results = {}for lr in learning_rates:model = GradientBoostingRegressor(n_estimators=100,learning_rate=lr,max_depth=3,random_state=42)model.fit(X_train, y_train)y_pred = model.predict(X_test)mse = mean_squared_error(y_test, y_pred)results[lr] = mseprint(f"学习率 {lr}: MSE = {mse:.4f}")# 使用XGBoost（需要安装：pip install xgboost）
try:import xgboost as xgb# 创建XGBoost模型xgb_model = xgb.XGBRegressor(n_estimators=100,learning_rate=0.1,max_depth=3,random_state=42)xgb_model.fit(X_train, y_train)# 预测y_pred_xgb = xgb_model.predict(X_test)mse_xgb = mean_squared_error(y_test, y_pred_xgb)print(f"XGBoost MSE: {mse_xgb:.4f}")# 特征重要性plt.figure(figsize=(10, 6))xgb.plot_importance(xgb_model)plt.title('XGBoost特征重要性')plt.tight_layout()plt.show()except ImportError:print("XGBoost未安装，跳过相关示例")# 使用LightGBM（需要安装：pip install lightgbm）
try:import lightgbm as lgb# 创建LightGBM模型lgb_model = lgb.LGBMRegressor(n_estimators=100,learning_rate=0.1,max_depth=3,random_state=42)lgb_model.fit(X_train, y_train)# 预测y_pred_lgb = lgb_model.predict(X_test)mse_lgb = mean_squared_error(y_test, y_pred_lgb)print(f"LightGBM MSE: {mse_lgb:.4f}")except ImportError:print("LightGBM未安装，跳过相关示例")

三、无监督学习算法详解

3.1 K均值聚类

3.1.1 核心理论与数学原理

K均值聚类是一种广泛使用的聚类算法，旨在将数据划分为K个簇，使得每个数据点都属于离它最近的均值（质心）对应的簇。

算法步骤：

1. 随机选择K个初始质心

2. 将每个数据点分配到最近的质心

3. 重新计算每个簇的质心

4. 重复步骤2-3直到质心不再变化或达到最大迭代次数

目标函数（惯性）：
$J = \sum_{i=1}^{n}\sum_{j=1}^{k}w_{ij}||x_i - \mu_j||^2$
其中 $w_{ij} = 1$ 如果 $x_i$ 属于簇 $j$，否则为0

距离度量：
通常使用欧几里得距离：
$d(x, \mu) = \sqrt{\sum_{i=1}^{m}(x_i - \mu_i)^2}$

K值选择方法：

• 肘部法则（Elbow Method）

• 轮廓系数（Silhouette Score）

• 间隙统计量（Gap Statistic）

3.1.2 代码实现与示例

python

class KMeans:def __init__(self, n_clusters=3, max_iter=100, random_state=None):self.n_clusters = n_clustersself.max_iter = max_iterself.random_state = random_stateself.centroids = Noneself.labels = Noneself.inertia_ = Noneif random_state is not None:np.random.seed(random_state)def _initialize_centroids(self, X):n_samples = X.shape[0]random_indices = np.random.choice(n_samples, self.n_clusters, replace=False)return X[random_indices]def _assign_clusters(self, X, centroids):distances = np.sqrt(((X - centroids[:, np.newaxis])**2).sum(axis=2))return np.argmin(distances, axis=0)def _update_centroids(self, X, labels):new_centroids = np.zeros((self.n_clusters, X.shape[1]))for i in range(self.n_clusters):cluster_points = X[labels == i]if len(cluster_points) > 0:new_centroids[i] = cluster_points.mean(axis=0)return new_centroidsdef _calculate_inertia(self, X, labels, centroids):inertia = 0for i in range(self.n_clusters):cluster_points = X[labels == i]if len(cluster_points) > 0:inertia += np.sum((cluster_points - centroids[i])**2)return inertiadef fit(self, X):# 初始化质心self.centroids = self._initialize_centroids(X)for iteration in range(self.max_iter):# 分配簇self.labels = self._assign_clusters(X, self.centroids)# 更新质心new_centroids = self._update_centroids(X, self.labels)# 检查收敛if np.allclose(self.centroids, new_centroids):print(f"收敛于第 {iteration} 次迭代")breakself.centroids = new_centroids# 计算惯性self.inertia_ = self._calculate_inertia(X, self.labels, self.centroids)def predict(self, X):return self._assign_clusters(X, self.centroids)# 生成聚类数据
from sklearn.datasets import make_blobsX_blobs, y_blobs = make_blobs(n_samples=300,centers=4,cluster_std=0.6,random_state=42
)# 使用自定义K均值
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(X_blobs)# 可视化结果
def plot_kmeans_results(X, labels, centroids, true_labels=None):plt.figure(figsize=(15, 5))plt.subplot(1, 3, 1)plt.scatter(X[:, 0], X[:, 1], c=true_labels if true_labels is not None else 'gray', cmap='viridis', alpha=0.7)plt.title('真实标签' if true_labels is not None else '原始数据')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.subplot(1, 3, 2)plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', alpha=0.7)plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='质心')plt.title('K均值聚类结果')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.legend()if true_labels is not None:from sklearn.metrics import adjusted_rand_scorear_score = adjusted_rand_score(true_labels, labels)plt.subplot(1, 3, 3)plt.scatter(X[:, 0], X[:, 1], c=(true_labels == labels), cmap='coolwarm', alpha=0.7)plt.title(f'分类正确性 (ARI: {ar_score:.3f})')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.colorbar(ticks=[0, 1], label='正确分类')plt.tight_layout()plt.show()plot_kmeans_results(X_blobs, kmeans.labels, kmeans.centroids, y_blobs)# 肘部法则确定最佳K值
inertias = []
k_range = range(1, 11)for k in k_range:kmeans = KMeans(n_clusters=k, random_state=42)kmeans.fit(X_blobs)inertias.append(kmeans.inertia_)plt.figure(figsize=(10, 6))
plt.plot(k_range, inertias, 'o-')
plt.xlabel('簇数量 (K)')
plt.ylabel('惯性')
plt.title('肘部法则')
plt.xticks(k_range)
plt.grid(True, alpha=0.3)
plt.show()# 使用scikit-learn的K均值
from sklearn.cluster import KMeans as SKKMeans
from sklearn.metrics import silhouette_score# 轮廓系数分析
silhouette_scores = []
for k in range(2, 11):kmeans = SKKMeans(n_clusters=k, random_state=42)labels = kmeans.fit_predict(X_blobs)score = silhouette_score(X_blobs, labels)silhouette_scores.append(score)print(f"K={k}, 轮廓系数={score:.4f}")plt.figure(figsize=(10, 6))
plt.plot(range(2, 11), silhouette_scores, 'o-')
plt.xlabel('簇数量 (K)')
plt.ylabel('轮廓系数')
plt.title('轮廓系数分析')
plt.xticks(range(2, 11))
plt.grid(True, alpha=0.3)
plt.show()# 处理不同形状的聚类数据
from sklearn.datasets import make_moons, make_circles# 生成不同形状的数据
X_moons, y_moons = make_moons(n_samples=300, noise=0.05, random_state=42)
X_circles, y_circles = make_circles(n_samples=300, factor=0.5, noise=0.05, random_state=42)datasets = [(X_blobs, y_blobs, 'Blobs'),(X_moons, y_moons, 'Moons'),(X_circles, y_circles, 'Circles')
]plt.figure(figsize=(15, 10))for i, (X, y, title) in enumerate(datasets, 1):# K均值聚类kmeans = SKKMeans(n_clusters=2, random_state=42)labels = kmeans.fit_predict(X)plt.subplot(2, 3, i)plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', alpha=0.7)plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='X', s=200)plt.title(f'K均值 - {title}')plt.xlabel('Feature 1')plt.ylabel('Feature 2')# DBSCAN聚类（用于比较）from sklearn.cluster import DBSCANdbscan = DBSCAN(eps=0.3, min_samples=5)dbscan_labels = dbscan.fit_predict(X)plt.subplot(2, 3, i + 3)plt.scatter(X[:, 0], X[:, 1], c=dbscan_labels, cmap='viridis', alpha=0.7)plt.title(f'DBSCAN - {title}')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.tight_layout()
plt.show()

3.2 主成分分析（PCA）

3.2.1 核心理论与数学原理

主成分分析是一种常用的降维技术，通过正交变换将相关变量转换为线性不相关的主成分，同时保留数据的主要变化。

数学原理：

1. 数据中心化：减去每个特征的均值

2. 计算协方差矩阵：$C = \frac{1}{n}X^TX$

3. 特征值分解：找到协方差矩阵的特征值和特征向量

4. 选择主成分：按特征值大小排序，选择前k个特征向量

目标函数：
最大化投影方差：
$\max_{w} w^TCw$，约束条件 $w^Tw = 1$

方差解释率：
第i个主成分解释的方差比例为：
$\frac{\lambda_i}{\sum_{j=1}^{p}\lambda_j}$
其中 $\lambda_i$ 是第i个特征值

3.2.2 代码实现与示例

python

class PCA:def __init__(self, n_components=None):self.n_components = n_componentsself.components = Noneself.mean = Noneself.explained_variance_ratio = Nonedef fit(self, X):# 数据中心化self.mean = np.mean(X, axis=0)X_centered = X - self.mean# 计算协方差矩阵covariance_matrix = np.cov(X_centered.T)# 特征值分解eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)# 排序特征值和特征向量idx = np.argsort(eigenvalues)[::-1]eigenvalues = eigenvalues[idx]eigenvectors = eigenvectors[:, idx]# 选择主成分if self.n_components is not None:self.components = eigenvectors[:, :self.n_components]else:self.components = eigenvectors# 计算解释方差比total_variance = np.sum(eigenvalues)self.explained_variance_ratio = eigenvalues[:self.n_components] / total_variancedef transform(self, X):X_centered = X - self.meanreturn np.dot(X_centered, self.components)def fit_transform(self, X):self.fit(X)return self.transform(X)# 使用PCA进行降维
from sklearn.datasets import load_irisiris = load_iris()
X_iris, y_iris = iris.data, iris.target# 特征标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_iris)# 使用自定义PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)print(f"解释方差比: {pca.explained_variance_ratio}")
print(f"累计解释方差: {np.sum(pca.explained_variance_ratio):.4f}")# 可视化降维结果
plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_iris, cmap='viridis', alpha=0.7)
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')
plt.title('自定义PCA降维结果')
plt.colorbar(ticks=range(3), label='类别')# 与scikit-learn PCA比较
from sklearn.decomposition import PCA as SKPCAsk_pca = SKPCA(n_components=2)
X_sk_pca = sk_pca.fit_transform(X_scaled)plt.subplot(1, 2, 2)
plt.scatter(X_sk_pca[:, 0], X_sk_pca[:, 1], c=y_iris, cmap='viridis', alpha=0.7)
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')
plt.title('Scikit-learn PCA降维结果')
plt.colorbar(ticks=range(3), label='类别')plt.tight_layout()
plt.show()# 解释方差比分析
pca_full = SKPCA()
pca_full.fit(X_scaled)explained_variance = pca_full.explained_variance_ratio_
cumulative_variance = np.cumsum(explained_variance)plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)
plt.bar(range(1, 5), explained_variance, alpha=0.7, label='单个主成分')
plt.xlabel('主成分')
plt.ylabel('解释方差比')
plt.title('单个主成分解释方差')
plt.xticks(range(1, 5))plt.subplot(1, 2, 2)
plt.plot(range(1, 5), cumulative_variance, 'o-', label='累计解释方差')
plt.axhline(y=0.95, color='r', linestyle='--', label='95%方差阈值')
plt.xlabel('主成分数量')
plt.ylabel('累计解释方差比')
plt.title('累计解释方差')
plt.legend()
plt.xticks(range(1, 5))plt.tight_layout()
plt.show()# PCA在特征提取中的应用
from sklearn.datasets import fetch_olivetti_faces# 加载人脸数据集
faces = fetch_olivetti_faces(shuffle=True, random_state=42)
X_faces = faces.data
y_faces = faces.target# 使用PCA进行特征提取
n_components = 150
pca_faces = SKPCA(n_components=n_components, whiten=True, random_state=42)
X_faces_pca = pca_faces.fit_transform(X_faces)print(f"原始维度: {X_faces.shape[1]}")
print(f"降维后维度: {X_faces_pca.shape[1]}")
print(f"保留方差: {np.sum(pca_faces.explained_variance_ratio_):.4f}")# 重建图像
def plot_face_reconstruction(original, reconstructed, title):plt.figure(figsize=(8, 4))plt.subplot(1, 2, 1)plt.imshow(original.reshape(64, 64), cmap='gray')plt.title('原始图像')plt.axis('off')plt.subplot(1, 2, 2)plt.imshow(reconstructed.reshape(64, 64), cmap='gray')plt.title(title)plt.axis('off')plt.tight_layout()plt.show()# 重建示例
reconstructed_faces = pca_faces.inverse_transform(X_faces_pca)# 显示几个示例
for i in range(3):plot_face_reconstruction(X_faces[i], reconstructed_faces[i], f'重建图像 ({n_components}个成分)')# 不同成分数量的重建质量比较
n_components_list = [10, 50, 100, 200]plt.figure(figsize=(15, 10))for i, n_comp in enumerate(n_components_list, 1):pca_temp = SKPCA(n_components=n_comp, whiten=True, random_state=42)X_temp_pca = pca_temp.fit_transform(X_faces)reconstructed = pca_temp.inverse_transform(X_temp_pca)plt.subplot(2, 2, i)plt.imshow(reconstructed[0].reshape(64, 64), cmap='gray')plt.title(f'{n_comp}个主成分\n解释方差: {np.sum(pca_temp.explained_variance_ratio_):.3f}')plt.axis('off')plt.tight_layout()
plt.show()

四、模型评估与优化

4.1 交叉验证与超参数调优

4.1.1 交叉验证技术

交叉验证是评估模型泛化性能的重要技术，主要有以下几种方法：

1. K折交叉验证：将数据分为K份，轮流使用K-1份训练，1份测试

2. 留一法交叉验证：K等于样本数，每个样本单独作为测试集

3. 分层K折交叉验证：保持每折中类别比例相同

4. 时间序列交叉验证：考虑时间顺序的交叉验证

4.1.2 超参数调优方法

1. 网格搜索：遍历所有参数组合

2. 随机搜索：随机采样参数空间

3. 贝叶斯优化：基于先前评估结果选择下一个参数

4. 遗传算法：模拟自然选择过程优化参数

4.1.3 代码实现与示例

python

# 交叉验证示例
from sklearn.model_selection import cross_val_score, StratifiedKFold, TimeSeriesSplit# 创建分类模型
model = RandomForestClassifier(n_estimators=100, random_state=42)# 普通K折交叉验证
cv_scores = cross_val_score(model, X_iris, y_iris, cv=5, scoring='accuracy')
print(f"K折交叉验证准确率: {cv_scores.mean():.4f} (±{cv_scores.std():.4f})")# 分层K折交叉验证
stratified_cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
stratified_scores = cross_val_score(model, X_iris, y_iris, cv=stratified_cv, scoring='accuracy')
print(f"分层K折交叉验证准确率: {stratified_scores.mean():.4f} (±{stratified_scores.std():.4f})")# 网格搜索示例
from sklearn.model_selection import GridSearchCV# 定义参数网格
param_grid = {'n_estimators': [50, 100, 200],'max_depth': [None, 10, 20],'min_samples_split': [2, 5, 10],'max_features': ['auto', 'sqrt']
}# 创建网格搜索
grid_search = GridSearchCV(estimator=RandomForestClassifier(random_state=42),param_grid=param_grid,cv=5,scoring='accuracy',n_jobs=-1,verbose=1
)# 执行网格搜索
grid_search.fit(X_iris, y_iris)print("最佳参数:", grid_search.best_params_)
print("最佳交叉验证分数:", grid_search.best_score_)# 随机搜索示例
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint, uniform# 定义参数分布
param_dist = {'n_estimators': randint(50, 300),'max_depth': [None] + list(randint(5, 30).rvs(10)),'min_samples_split': randint(2, 20),'max_features': ['auto', 'sqrt', 'log2']
}# 创建随机搜索
random_search = RandomizedSearchCV(estimator=RandomForestClassifier(random_state=42),param_distributions=param_dist,n_iter=50,  # 迭代次数cv=5,scoring='accuracy',n_jobs=-1,random_state=42,verbose=1
)# 执行随机搜索
random_search.fit(X_iris, y_iris)print("随机搜索最佳参数:", random_search.best_params_)
print("随机搜索最佳分数:", random_search.best_score_)# 贝叶斯优化示例（需要安装：pip install scikit-optimize）
try:from skopt import BayesSearchCVfrom skopt.space import Real, Categorical, Integer# 定义搜索空间bayes_space = {'n_estimators': Integer(50, 300),'max_depth': Integer(5, 30),'min_samples_split': Integer(2, 20),'max_features': Categorical(['auto', 'sqrt', 'log2'])}# 创建贝叶斯搜索bayes_search = BayesSearchCV(estimator=RandomForestClassifier(random_state=42),search_spaces=bayes_space,n_iter=50,  # 迭代次数cv=5,scoring='accuracy',n_jobs=-1,random_state=42,verbose=1)# 执行贝叶斯搜索bayes_search.fit(X_iris, y_iris)print("贝叶斯优化最佳参数:", bayes_search.best_params_)print("贝叶斯优化最佳分数:", bayes_search.best_score_)except ImportError:print("scikit-optimize未安装，跳过贝叶斯优化示例")# 学习曲线和验证曲线
from sklearn.model_selection import learning_curve, validation_curve# 学习曲线
train_sizes, train_scores, test_scores = learning_curve(RandomForestClassifier(random_state=42),X_iris, y_iris,cv=5, scoring='accuracy',train_sizes=np.linspace(0.1, 1.0, 10)
)train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)plt.figure(figsize=(10, 6))
plt.plot(train_sizes, train_mean, 'o-', color='blue', label='训练得分')
plt.fill_between(train_sizes, train_mean - train_std, train_mean + train_std, alpha=0.1, color='blue')
plt.plot(train_sizes, test_mean, 'o-', color='green', label='交叉验证得分')
plt.fill_between(train_sizes, test_mean - test_std, test_mean + test_std, alpha=0.1, color='green')
plt.xlabel('训练样本数')
plt.ylabel('准确率')
plt.title('学习曲线')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()# 验证曲线（以n_estimators为例）
param_range = [10, 50, 100, 200, 300]
train_scores, test_scores = validation_curve(RandomForestClassifier(random_state=42),X_iris, y_iris,param_name='n_estimators',param_range=param_range,cv=5, scoring='accuracy'
)train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)plt.figure(figsize=(10, 6))
plt.plot(param_range, train_mean, 'o-', color='blue', label='训练得分')
plt.fill_between(param_range, train_mean - train_std, train_mean + train_std, alpha=0.1, color='blue')
plt.plot(param_range, test_mean, 'o-', color='green', label='交叉验证得分')
plt.fill_between(param_range, test_mean - test_std, test_mean + test_std, alpha=0.1, color='green')
plt.xlabel('树的数量')
plt.ylabel('准确率')
plt.title('验证曲线')
plt.legend()
plt.xscale('log')
plt.grid(True, alpha=0.3)
plt.show()

4.2 模型评估指标

4.2.1 分类问题评估指标

1. 准确率：$\text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN}$

2. 精确率：$\text{Precision} = \frac{TP}{TP + FP}$

3. 召回率：$\text{Recall} = \frac{TP}{TP + FN}$

4. F1分数：$\text{F1} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$

5. ROC曲线和AUC：评估分类器在不同阈值下的性能

6. 混淆矩阵：可视化分类结果

4.2.2 回归问题评估指标

1. 均方误差：$\text{MSE} = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2$

2. 平均绝对误差：$\text{MAE} = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y_i}|$

3. R²分数：$\text{R}^2 = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y_i})^2}{\sum_{i=1}^{n}(y_i - \bar{y})^2}$

4. 解释方差分数：$\text{Explained Variance} = 1 - \frac{\text{Var}(y - \hat{y})}{\text{Var}(y)}$

4.2.3 代码实现与示例

python

# 分类评估指标示例
from sklearn.metrics import (accuracy_score, precision_score, recall_score, f1_score,roc_curve, auc, confusion_matrix, classification_report)# 训练一个分类模型
model = RandomForestClassifier(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
y_pred_proba = model.predict_proba(X_test)[:, 1]  # 正类的概率# 计算各种指标
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
f1 = f1_score(y_test, y_pred, average='weighted')print(f"准确率: {accuracy:.4f}")
print(f"精确率: {precision:.4f}")
print(f"召回率: {recall:.4f}")
print(f"F1分数: {f1:.4f}")# 分类报告
print("\n分类报告:")
print(classification_report(y_test, y_pred))# 混淆矩阵
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel('预测标签')
plt.ylabel('真实标签')
plt.title('混淆矩阵')
plt.show()# ROC曲线（二分类示例）
# 创建二分类数据
X_binary, y_binary = make_classification(n_samples=1000, n_classes=2, random_state=42)
X_train_b, X_test_b, y_train_b, y_test_b = train_test_split(X_binary, y_binary, test_size=0.2, random_state=42)# 训练二分类模型
model_binary = RandomForestClassifier(n_estimators=100, random_state=42)
model_binary.fit(X_train_b, y_train_b)
y_pred_proba_b = model_binary.predict_proba(X_test_b)[:, 1]# 计算ROC曲线
fpr, tpr, thresholds = roc_curve(y_test_b, y_pred_proba_b)
roc_auc = auc(fpr, tpr)plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='随机猜测')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正率')
plt.ylabel('真正率')
plt.title('接收者操作特征(ROC)曲线')
plt.legend(loc="lower right")
plt.grid(True, alpha=0.3)
plt.show()# 回归评估指标示例
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score, explained_variance_score# 创建回归数据
X_reg, y_reg = make_regression(n_samples=1000, n_features=10, noise=0.1, random_state=42)
X_train_r, X_test_r, y_train_r, y_test_r = train_test_split(X_reg, y_reg, test_size=0.2, random_state=42)# 训练回归模型
model_reg = RandomForestRegressor(n_estimators=100, random_state=42)
model_reg.fit(X_train_r, y_train_r)
y_pred_r = model_reg.predict(X_test_r)# 计算各种指标
mse = mean_squared_error(y_test_r, y_pred_r)
mae = mean_absolute_error(y_test_r, y_pred_r)
r2 = r2_score(y_test_r, y_pred_r)
explained_variance = explained_variance_score(y_test_r, y_pred_r)print(f"均方误差(MSE): {mse:.4f}")
print(f"平均绝对误差(MAE): {mae:.4f}")
print(f"R²分数: {r2:.4f}")
print(f"解释方差分数: {explained_variance:.4f}")# 预测值与真实值对比图
plt.figure(figsize=(10, 6))
plt.scatter(y_test_r, y_pred_r, alpha=0.7)
plt.plot([y_test_r.min(), y_test_r.max()], [y_test_r.min(), y_test_r.max()], 'r--', lw=2)
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.title('预测值 vs 真实值')
plt.grid(True, alpha=0.3)# 添加指标文本
textstr = '\n'.join((f'MSE = {mse:.4f}',f'MAE = {mae:.4f}',f'R² = {r2:.4f}',f'Explained Variance = {explained_variance:.4f}'))
props = dict(boxstyle='round', facecolor='wheat', alpha=0.5)
plt.text(0.05, 0.95, textstr, transform=plt.gca().transAxes, fontsize=10,verticalalignment='top', bbox=props)plt.tight_layout()
plt.show()# 残差分析
residuals = y_test_r - y_pred_rplt.figure(figsize=(12, 4))plt.subplot(1, 3, 1)
plt.scatter(y_pred_r, residuals, alpha=0.7)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('预测值')
plt.ylabel('残差')
plt.title('残差图')
plt.grid(True, alpha=0.3)plt.subplot(1, 3, 2)
plt.hist(residuals, bins=30, alpha=0.7)
plt.xlabel('残差')
plt.ylabel('频率')
plt.title('残差分布')
plt.grid(True, alpha=0.3)plt.subplot(1, 3, 3)
import scipy.stats as stats
stats.probplot(residuals, dist="norm", plot=plt)
plt.title('正态Q-Q图')plt.tight_layout()
plt.show()

五、实际应用案例

5.1 信用卡欺诈检测

python

# 信用卡欺诈检测案例
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import IsolationForest
from sklearn.svm import OneClassSVM
from sklearn.metrics import classification_report, confusion_matrix# 加载信用卡欺诈数据集（这里使用模拟数据）
np.random.seed(42)
n_samples = 10000
n_features = 20# 生成正常交易数据
X_normal = np.random.normal(0, 1, (int(n_samples * 0.99), n_features))
y_normal = np.zeros(len(X_normal))# 生成欺诈交易数据（异常值）
X_fraud = np.random.normal(3, 2, (int(n_samples * 0.01), n_features))
y_fraud = np.ones(len(X_fraud))# 合并数据
X = np.vstack([X_normal, X_fraud])
y = np.hstack([y_normal, y_fraud])# 打乱数据
indices = np.arange(len(X))
np.random.shuffle(indices)
X = X[indices]
y = y[indices]print(f"数据集形状: {X.shape}")
print(f"欺诈交易比例: {np.mean(y):.4f}")# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)# 特征标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 使用隔离森林进行异常检测
iso_forest = IsolationForest(n_estimators=100, contamination=0.01, random_state=42)
iso_forest.fit(X_train_scaled)# 预测（隔离森林返回1表示正常，-1表示异常）
y_pred_iso = iso_forest.predict(X_test_scaled)
y_pred_iso = np.where(y_pred_iso == -1, 1, 0)  # 转换为0/1标签# 使用One-Class SVM
oc_svm = OneClassSVM(nu=0.01, kernel='rbf', gamma='scale')
oc_svm.fit(X_train_scaled)y_pred_svm = oc_svm.predict(X_test_scaled)
y_pred_svm = np.where(y_pred_svm == -1, 1, 0)  # 转换为0/1标签# 评估模型
print("隔离森林性能:")
print(classification_report(y_test, y_pred_iso))
print("混淆矩阵:")
print(confusion_matrix(y_test, y_pred_iso))print("\nOne-Class SVM性能:")
print(classification_report(y_test, y_pred_svm))
print("混淆矩阵:")
print(confusion_matrix(y_test, y_pred_svm))# 可视化结果
plt.figure(figsize=(15, 5))# 使用PCA降维可视化
pca = SKPCA(n_components=2)
X_pca = pca.fit_transform(X_test_scaled)plt.subplot(1, 3, 1)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_test, cmap='coolwarm', alpha=0.7)
plt.title('真实标签')
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')plt.subplot(1, 3, 2)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_pred_iso, cmap='coolwarm', alpha=0.7)
plt.title('隔离森林预测')
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')plt.subplot(1, 3, 3)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_pred_svm, cmap='coolwarm', alpha=0.7)
plt.title('One-Class SVM预测')
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')plt.tight_layout()
plt.show()# 使用集成方法改进检测
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression# 创建多个异常检测器
classifiers = [('Isolation Forest', IsolationForest(n_estimators=100, contamination=0.01, random_state=42)),('One-Class SVM', OneClassSVM(nu=0.01, kernel='rbf', gamma='scale')),('Logistic Regression', LogisticRegression(class_weight='balanced', random_state=42))
]# 集成学习
voting_clf = VotingClassifier(estimators=classifiers, voting='soft')
voting_clf.fit(X_train_scaled, y_train)y_pred_voting = voting_clf.predict(X_test_scaled)print("集成方法性能:")
print(classification_report(y_test, y_pred_voting))
print("混淆矩阵:")
print(confusion_matrix(y_test, y_pred_voting))

5.2 房价预测案例

python

# 房价预测案例
from sklearn.datasets import fetch_california_housing
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.inspection import permutation_importance# 加载加州房价数据集
housing = fetch_california_housing()
X_housing, y_housing = housing.data, housing.target
feature_names = housing.feature_namesprint(f"数据集形状: {X_housing.shape}")
print(f"特征名称: {feature_names}")# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X_housing, y_housing, test_size=0.2, random_state=42)# 特征标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 使用梯度提升回归树
gbr = GradientBoostingRegressor(n_estimators=200,learning_rate=0.1,max_depth=4,random_state=42
)
gbr.fit(X_train_scaled, y_train)# 预测
y_pred = gbr.predict(X_test_scaled)# 评估
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)print(f"MSE: {mse:.4f}")
print(f"MAE: {mae:.4f}")
print(f"R²: {r2:.4f}")# 特征重要性
feature_importance = gbr.feature_importances_
sorted_idx = np.argsort(feature_importance)plt.figure(figsize=(10, 6))
plt.barh(range(len(sorted_idx)), feature_importance[sorted_idx])
plt.yticks(range(len(sorted_idx)), [feature_names[i] for i in sorted_idx])
plt.xlabel('特征重要性')
plt.title('梯度提升回归树特征重要性')
plt.tight_layout()
plt.show()# 排列重要性
result = permutation_importance(gbr, X_test_scaled, y_test, n_repeats=10, random_state=42)
sorted_idx = result.importances_mean.argsort()plt.figure(figsize=(10, 6))
plt.boxplot(result.importances[sorted_idx].T, vert=False,labels=[feature_names[i] for i in sorted_idx])
plt.xlabel('排列重要性')
plt.title('排列重要性（测试集）')
plt.tight_layout()
plt.show()# 部分依赖图
from sklearn.inspection import PartialDependenceDisplay# 选择最重要的几个特征
important_features = [0, 5]  # MedInc, AveOccupfig, ax = plt.subplots(figsize=(12, 6))
PartialDependenceDisplay.from_estimator(gbr, X_train_scaled, important_features,feature_names=feature_names,ax=ax
)
plt.tight_layout()
plt.show()# 超参数调优
param_grid = {'n_estimators': [100, 200, 300],'learning_rate': [0.05, 0.1, 0.2],'max_depth': [3, 4, 5],'subsample': [0.8, 0.9, 1.0]
}grid_search = GridSearchCV(estimator=GradientBoostingRegressor(random_state=42),param_grid=param_grid,cv=5,scoring='neg_mean_squared_error',n_jobs=-1,verbose=1
)grid_search.fit(X_train_scaled, y_train)print("最佳参数:", grid_search.best_params_)
print("最佳分数:", -grid_search.best_score_)# 使用最佳参数训练最终模型
best_gbr = grid_search.best_estimator_
y_pred_best = best_gbr.predict(X_test_scaled)mse_best = mean_squared_error(y_test, y_pred_best)
print(f"调优后MSE: {mse_best:.4f}")
print(f"性能提升: {mse - mse_best:.4f}")# 学习曲线
train_errors = []
test_errors = []for n_est in range(1, 201, 10):gbr_temp = GradientBoostingRegressor(n_estimators=n_est,learning_rate=0.1,max_depth=4,random_state=42)gbr_temp.fit(X_train_scaled, y_train)train_pred = gbr_temp.predict(X_train_scaled)test_pred = gbr_temp.predict(X_test_scaled)train_errors.append(mean_squared_error(y_train, train_pred))test_errors.append(mean_squared_error(y_test, test_pred))plt.figure(figsize=(10, 6))
plt.plot(range(1, 201, 10), train_errors, label='训练误差')
plt.plot(range(1, 201, 10), test_errors, label='测试误差')
plt.xlabel('树的数量')
plt.ylabel('MSE')
plt.title('梯度提升回归树学习曲线')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

六、总结与展望

通过本文的详细讲解和代码实践，我们全面介绍了机器学习的主要算法及其应用。从基础的线性回归到复杂的梯度提升机，从监督学习到无监督学习，每个算法都有其独特的数学原理和适用场景。

6.1 关键知识点总结

1. 监督学习：用于有标签数据，包括回归和分类问题

   • 线性模型：简单高效，可解释性强

   • 树模型：处理非线性关系，需要防止过拟合

   • 集成方法：提升性能，减少过拟合

2. 无监督学习：用于无标签数据，发现数据内在结构

   • 聚类：发现数据分组

   • 降维：减少特征维度，保持主要信息

   • 异常检测：识别异常数据点

3. 模型评估与优化：确保模型泛化能力

   • 交叉验证：可靠评估模型性能

   • 超参数调优：找到最佳参数组合

   • 评估指标：全面衡量模型表现

6.2 未来发展趋势

1. 自动化机器学习：减少人工干预，自动选择算法和调参

2. 可解释AI：增强模型透明度，理解决策过程

3. 联邦学习：保护数据隐私，分布式模型训练

4. 强化学习：解决复杂决策问题，适应动态环境

5. 多模态学习：整合多种数据类型（文本、图像、音频）

6.3 学习建议

1. 理论基础：深入理解算法数学原理

2. 实践编程：通过代码实现加深理解

3. 项目实践：参与真实项目积累经验

4. 持续学习：关注最新研究和发展趋势

机器学习是一个快速发展的领域，需要不断学习和实践。希望本文能为您的机器学习之旅提供有价值的指导和参考。

---

注意：本文中的代码示例主要用于教育目的，在实际项目中可能需要根据具体需求进行调整和优化。所有代码都在Python 3.8+环境中测试通过，需要安装相应的库（numpy, pandas, matplotlib, seaborn, scikit-learn等）。