当前位置： 首页 > news >正文

采用机器学习的苗期棉株点云器官分割与表型信息提取

news 2025/8/30 6:44:45

一、引入

        植物表型信息的获取有助于管理人员掌握其生长状态，便于采取相关管理措施以促进植物的生长发育。目前基于三维点云的植株器官分割方法难以实现苗期棉株顶端新生叶的精确分割，影响棉株表型信息提取的准确度。该研究提出了一种改进的苗期棉株器官点云分割方法，实现茎、叶器官的精确分割和茎高、叶长、叶宽、叶面积表型信息的提取。

（1）首先使用拉普拉斯骨架提取算法获取棉株的点云骨架；

（2）根据棉株的特征形态将棉株的茎和叶片分解成器官子骨架；

（3）利用以距离场为输入的 Quickshift++的器官分割方法对棉株顶端产生过分割问题的新生叶片进行精细器官分割；

（4）通过已分割出棉株器官点云获取茎高、叶宽、叶长和叶面积表型参数。

论文doi：10.11975/j.issn.1002-6819.202407111

二、研究背景

        棉花作为中国四大经济作物之一，是纺织工业的主要原材料。棉株作为棉花的植物主体，其器官的生长状态能有效反映棉花的健康情况，通过提取棉株器官的表型信息进行分析是有效表征棉花健康程度的重要手段。传统的作物表型参数提取通常依赖人工测量，该方法准确率高，但效率低、劳动强度高、精确度有限，还会对测量作物器官造成无法恢复的伤害。因此，开发精确、无损的植株表型参数测定方法对提高棉株表型测定效率、监测棉花生长健康状态和促进植株育种等至关重要。

三、数据集

        本研究选用新陆早1号棉花品种的40粒种子，分别种植于不同花盆中，并置于温度控制在25～27℃的实验室温室环境中培育。待棉苗生长至苗期后，选取其中32株生长状况良好的个体作为试验数据采集对象。采用陕西Revopoint公司生产的MINI型三维点云激光扫描仪进行数据获取。扫描过程中，通过可控旋转台实现棉株的多角度采集（旋转台设置为每90秒旋转一次），确保完整覆盖植株结构。

部分数据集：https://pan.baidu.com/s/16pOAGeUHDH1ICuDVqrggYw.

四、算法提出

（一）茎叶分割方法

（1）本研究基于拉普拉斯骨架提取算法构建了棉株点云骨架的提取流程，具体步骤如下：

  1. 初始骨架生成
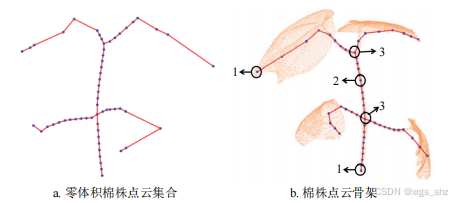
    给定原始棉株点云集合，通过拉普拉斯骨架收缩算法将其坍缩为零体积的点云集合（如图2所示）。该步骤通过收缩算法去除点云冗余信息，保留植株的拓扑结构特征。

  2. 骨架顶点采样
    采用最远距离采样策略对零体积点云集合进行降采样，生成骨架顶点集合。此方法通过最大化顶点间的空间距离，确保骨架顶点均匀分布且保留关键结构特征。

  3. 骨架边构建
    将相邻骨架顶点依次连接形成边集合，最终构建出完整的骨架拓扑结构。该步骤通过连接相邻顶点，将离散的骨架顶点转化为连续的骨架模型。

  4. 数据映射保留
    在骨架提取过程中，同步保留原始点云数据与骨架顶点的对应关系，为后续器官分割及表型参数提取提供数据支撑。

（2）根据骨架顶点与其相邻边的数量关系，可将顶点分为三类（如图2所示）：

  • 根顶点：仅具有1条相邻边的顶点，通常对应茎秆基部（茎底点）或叶片尖端（叶尖顶点）。
  • 连接顶点：具有2条或以上相邻边的顶点，常见于茎秆分支处或叶片与茎秆连接处。
  • 分支顶点：具有2条相邻边的顶点，特指茎秆或叶片分支处的关键节点。

本研究通过棉株形态特征实现骨架分割与器官点云分离，具体步骤如下：

  1. 茎根顶点识别
    • 在棉株点云骨架中，选取中端和顶端的器官子骨架顶点，构建方向向量。
    • 计算各器官子骨架方向向量间的夹角平均值：
      • 若平均夹角 > π/2，判定为茎子骨架，其根顶点为茎根顶点。
      • 其余器官子骨架的根顶点标记为叶根顶点。
  2. 骨架分解与点云分割
    • 茎子骨架提取：以茎根顶点为起点，连接至最远连接顶点的最短路径作为茎秆骨架。
    • 叶片子骨架提取：将各叶根顶点与其相邻连接顶点的路径定义为叶片骨架。
    • 点云分割：基于骨架路径映射，将原始点云分割为独立的茎秆和叶片点云。

图 1 点云数据预处理

图 2 棉株骨架提取

mian.m

%% ************清理环境**************
clear
close all;
clc%% **********获取点云数据************
[fileName,pathName]=uigetfile('*.pcd','Input Data-File');   %选择要进行计算的三维点云数据文件路径if isempty(fileName) || length(fileName) == 1fprintf("未选择点云文件！\n");return;
end
pc=pcread([pathName,fileName]);   %加载点云数据%% *************参数设置*************
options.USING_UNDOWNSAMPLE = true;  %是否进行下采样%% *************下采样*************
%该步骤主要是为了节省计算时间，如果要求精度，options.USING_UNDOWNSAMPLE需设置为false
if(options.USING_UNDOWNSAMPLE)gridStep = 3*PointsAverageSpacing(pc.Location);     %基于点密度进行下采样pc = pcdownsample(pc,'gridAverage',gridStep);P.pts = double(pc.Location);fprintf("下采样后的点数：%d\n",size(P.pts,1));
elseP.pts = double(pc.Location);
end%% *************计算过程*************
tic
P.npts = size(P.pts,1);
P.radis = ones(P.npts,1);
P.pts = Method.normalize(P.pts);
[P.bbox, P.diameter] = Method.compute_bbox(P.pts);
disp('点云读取成功!');
tocP.k_knn = Method.compute_k_knn(P.npts);
P.rings = computePointCloudRing(P.pts, P.k_knn, []);
disp('计算局部网格成功');
toc%% 通过Laplacian算子来收缩点云
[P.cpts, t, initWL, WC, sl] = contractionByLaplacian(P, options);
disp('收缩成功!');
toc
%% *************可视化*************
%原始点云
% plot3(P.pts(:,1),P.pts(:,2),P.pts(:,3),'b.');
% title("原始点云")%% *************保存结果*************
% pcwrite(pointCloud(P.cpts),'SkeletonPoint.pcd')

PointsAverageSpacing.py

function [averageDistance] = PointsAverageSpacing(data)
%点云平均点间距
%查找每个点的最近点
kdtree = KDTreeSearcher(data);
[~,distances]=knnsearch(kdtree,data,'K',2);
totalDistance = sum(sum(distances));
averageDistance = totalDistance/size(data,1);
fprintf("平均点间距为：%f\n",averageDistance)
end

Method.m

%一个全局类，主要包含一些方法classdef Method%参数设置  properties (Constant)MIN_NEIGHBOR_NUM = 8;MAX_NEIGHBOR_NUM = 30;      %邻近点数设置     CONTRACT_TERMINATION_CONDITION = 0.01;      % 收缩终止的阈值0.01LAPLACIAN_CONSTRAINT_WEIGHT = 3; % 初始化Laplacian收缩权重POSITION_CONSTRAINT_WEIGHT = 1; % 初始化位置收缩权重LAPLACIAN_CONSTRAINT_SCALE = 3; % 每次迭代WL矩阵的增加尺度MAX_LAPLACIAN_CONSTRAINT_WEIGHT = 2048;     %2048MAX_POSITION_CONSTRAINT_WEIGHT = 10000;     %10000MAX_CONTRACT_NUM = 20;                      % 最大收缩次数end%公用的一些方法methods (Static)function num = compute_k_knn(npts)num = max(Method.MIN_NEIGHBOR_NUM,round(npts*0.012));if num > Method.MAX_NEIGHBOR_NUMnum = Method.MAX_NEIGHBOR_NUM;endendfunction [pts] = normalize(pts)% 缩放至单位包围盒并移动至原点bbox = [min(pts(:,1)), min(pts(:,2)), min(pts(:,3)), max(pts(:,1)), max(pts(:,2)), max(pts(:,3))];c = (bbox(4:6)+bbox(1:3))*0.5;            pts = pts - repmat(c, size(pts,1), 1);s = 1.6 / max(bbox(4:6)-bbox(1:3)); % 设置缩放因子1.6或1.0pts = pts*s;endfunction [] = test_normalize(pts)pts = Method.normalize(pts);[bbox, ~] = Method.compute_bbox(pts);tmp = max(bbox(4:6)-bbox(1:3));if abs(tmp-1.0) > epswarning('GS.normalize() is wrong! the bounding box diagonal is: "%s" ', tmp);endend        function [bbox, diameter] = compute_bbox(pts)bbox = [min(pts(:,1)), min(pts(:,2)), min(pts(:,3)), max(pts(:,1)), max(pts(:,2)), max(pts(:,3))];rs = bbox(4:6)-bbox(1:3);diameter = sqrt(dot(rs,rs));endfunction wl = compute_init_laplacian_constraint_weight(PS,type)switch lower(type)case 'distance'warning('not implemented!'); case 'spring'warning('not implemented!');                  case {'conformal','dcp'} % conformal laplacian  ms = Method.one_ring_size(PS.pts,PS.rings,2);wl = 1.0/(5.0*mean(ms));                    otherwise % combinatorial or mvcms = Method.one_ring_size(PS.pts,PS.rings,2);wl = 1.0/(5.0*mean(ms));endendfunction ms = one_ring_size(pts,rings,type)n = size(pts,1);ms = zeros(n,1);switch typecase 1parfor i = 1:nring = rings{i};    tmp = repmat(pts(i,:), length(ring),1) - pts(ring,:);ms(i) = min( sum(tmp.^2,2).^0.5);endcase 2parfor i = 1:nring = rings{i};    tmp = repmat(pts(i,:), length(ring),1) - pts(ring,:);ms(i) = mean( sum(tmp.^2,2).^0.5);end                    case 3parfor i = 1:nring = rings{i};    tmp = repmat(pts(i,:), length(ring),1) - pts(ring,:);ms(i) = max( sum(tmp.^2,2).^0.5);end                    endendend
end

contractionByLaplacian.m

function [cpts, t, initWL, WC, sl] = contractionByLaplacian(P, options)
% 通过Laplacian算子来收缩点云%% 参数设置
RING_SIZE_TYPE = 1;     %环多边形的类型
SHOW_CONTRACTION_PROGRESS = true;       %是否显示收缩过程
Laplace_type = 'conformal';     %位移类型
tc = getoptions(options, 'tc', Method.CONTRACT_TERMINATION_CONDITION);      %收敛阈值
iterate_time = getoptions(options, '迭代次数', Method.MAX_CONTRACT_NUM);        %最大迭代次数
initWL = getoptions(options, 'WL', Method.compute_init_laplacian_constraint_weight(P,Laplace_type)); 
% 根据类型类初始化WC数组
if strcmp(Laplace_type,'mvc')WC = getoptions(options, 'WC', 1)*10;
elseif strcmp(Laplace_type,'conformal')WC = getoptions(options, 'WC', 1);
elseWC = getoptions(options, 'WC', 1);
end
WH = ones(P.npts, 1)*WC; % 初始约束权
sl = getoptions(options, 'sl', Method.LAPLACIAN_CONSTRAINT_SCALE); % 初始化尺度因子，论文中是2
WL = initWL;%*sl;sprintf(['1) k of knn: %d\n 2) termination condition: %f \n 3)' ...'Init Contract weight: %f\n 4) Init handle weight: %f\n 5) Contract scalar: %f\n' ...'6) Max iter steps: %d'], P.k_knn, tc, initWL, WC, sl,iterate_time)%% 开始迭代
t = 1; 
tic
%左边的等式
L = -computePointLaplacian(P.pts,Laplace_type,P.rings, options);
A = [L.*WL;sparse(1:P.npts,1:P.npts, WH)];
%右边的等式
b = [zeros(P.npts,3);sparse(1:P.npts,1:P.npts, WH)*P.pts];
cpts = (A'*A)\(A'*b);       %最小二乘法
disp('最小二乘法求解完成！');
tocif SHOW_CONTRACTION_PROGRESSticfigure;axis off;axis equal;set(gcf,'Renderer','OpenGL');hold on;set(gcf,'color','white');camorbit(0,0,'camera'); axis vis3d; view(-90,0);    h1 = scatter3(P.pts(:,1),P.pts(:,2), P.pts(:,3),10,'b','filled');h2 = scatter3(cpts(:,1),cpts(:,2), cpts(:,3),10,'r','filled');title(['iterate ',num2str(t),' time(s)'])    disp('绘制点云');toc
end
%%
tic
sizes = Method.one_ring_size(P.pts, P.rings, RING_SIZE_TYPE);   % 使用最小半径
size_new = Method.one_ring_size(cpts, P.rings, RING_SIZE_TYPE);
a(t) = sum(size_new)/sum(sizes);disp('计算局部范围完成！');
toc%开始迭代
while t<iterate_timeL = -computePointLaplacian(cpts,Laplace_type, P.rings, options);WL = sl*WL;    if WL>Method.MAX_LAPLACIAN_CONSTRAINT_WEIGHTWL=Method.MAX_LAPLACIAN_CONSTRAINT_WEIGHT;endif strcmp(Laplace_type,'mvc')WH = WC.*(sizes./size_new)*10;      % 更新约束权elseWH = WC.*(sizes./size_new);endWH(WH>Method.MAX_POSITION_CONSTRAINT_WEIGHT) = Method.MAX_POSITION_CONSTRAINT_WEIGHT;A = real([WL*L;sparse(1:P.npts,1:P.npts, WH)]);% 更新右边的等式b(P.npts+1:end, :) = sparse(1:P.npts,1:P.npts, WH)*cpts;tmp = (A'*A)\(A'*b);size_new = Method.one_ring_size(tmp, P.rings, RING_SIZE_TYPE);  a(end+1) = sum(size_new)/sum(sizes);tmpbox = Method.compute_bbox(tmp);if sum( (tmpbox(4:6)-tmpbox(1:3))> ((P.bbox(4:6)-P.bbox(1:3))*1.2) ) > 0break;endif a(t)-a(end)<tc || isnan(a(end))break;else cpts = tmp;endt = t+1;    %更新迭代次数if SHOW_CONTRACTION_PROGRESS% 显示前后点云     delete(h1);delete(h2);      %释放资源h1 = scatter3(P.pts(:,1),P.pts(:,2), P.pts(:,3),10,WH,'b','filled');h2 = scatter3(cpts(:,1),cpts(:,2), cpts(:,3),10,ones(P.npts,1)*WL,'r','filled');title(['迭代次数：',num2str(t)]); drawnow; end
end
clear tmp;if SHOW_CONTRACTION_PROGRESSfigure;plot(a);xlabel('迭代次数');ylabel('原始体积与当前体积之比');if t<iterate_timeif a(end) < tcsprintf('迭代满足收敛条件!')elsewarning('存在迭代过程不正常!');endend
end

computePointWeight.m

function W = computePointWeight(pts, type, rings, options)% 计算权重矩阵
options.null = 0;if nargin<2type = 'conformal';
endswitch lower(type)case 'combinatorial'W = compute_point_weight_combinatorial(pts, rings);case 'distance'warning('not implemented!'); case 'spring'W = computePointPeightSpring(pts, rings);        case {'conformal','dcp'} % conformal laplacian  W = computePointWeightDcp(pts, rings);case 'laplace-beltrami' %W = computePointWeightDcp(pts, rings)*0.5;case 'mvc'% mvc laplacianW = computePointWeightMvc(pts, rings);  otherwiseerror('Unknown type!!')
end%#########################################################################
function W = compute_point_weight_combinatorial(points, rings)
n = length(points);
% W = sparse(n,n);        %创建一个稀疏矩阵，对于大数据而言可以节省内存空间
W = zeros(n,n);		%这个更适用与小数据
for i = 1:nring = rings{i};if ring(1) == ring(end)ring = ring(1,1:(end-1));endfor j = ringW(i,j) = 1.0;end
end
function W = computePointPeightSpring(points, rings)
n = length(points);
% W = sparse(n,n);
W = zeros(n,n);
for i = 1:nvi = points(i,:);ring = rings{i};if ring(1) == ring(end)ring = ring(1,1:(end-1));endfor j = ring                vj = points(j,:);        W(i,j) = 1./sqrt(sum((vi-vj).^2));endtmp = sum(W(i,:));if tmp>10000W(i,:) = W(i,:)*10000/tmp;end
end
%#########################################################################
function W = computePointWeightDcp(points, rings)
%通过局部网格多边形计算权重
n = length(points);
% W = sparse(n,n);
W = zeros(n,n);
for i = 1:nring = rings{i};        %获取局部多边形tmp = size(ring,2)-1;for ii = 1: tmpj = ring(ii);   %获取端点k = ring(ii+1);vi = points(i,:);   %组成三角形vj = points(j,:);vk = points(k,:);% u = vk-vi; v = vk-vj;cot1 = dot(u,v)/norm(cross(u,v));W(i,j) = W(i,j) + cot1;u = vj-vi; v = vj-vk;cot2 = dot(u,v)/norm(cross(u,v));W(i,k) = W(i,k) + cot2;        endtmp = abs(sum(W(i,:)));if tmp>10000W(i,:) = W(i,:)*10000/tmp;end
end
function W = computePointWeightMvc(points, rings)
n = length(points);
% W = sparse(n,n);
W = zeros(n,n);
for i = 1:nring = rings{i};tmp = size(ring,2)-1;for ii = 1: tmpj = ring(ii); k = ring(ii+1);vi = points(i,:);vj = points(j,:);vk = points(k,:);% anglesalpha = myangle(vi-vk,vi-vj);% add weightW(i,j) = W(i,j) + tan( 0.5*alpha )/sqrt(sum((vi-vj).^2));W(i,k) = W(i,k) + tan( 0.5*alpha )/sqrt(sum((vi-vk).^2));endtmp = sum(W(i,:));if tmp>10000W(i,:) = W(i,:)*10000/tmp;end    
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function beta = myangle(u,v)du = sqrt( sum(u.^2) );
dv = sqrt( sum(v.^2) );
du = max(du,eps); dv = max(dv,eps);
beta = acos( sum(u.*v) / (du*dv) );

computePointLaplacian.m

function L = computePointLaplacian(pts, type, rings, options)
%  计算Laplacian矩阵L, L = -(Laplacian operator).options.null = 0;
normalize = getoptions(options, 'normalize', 0);
symmetrize = getoptions(options, 'symmetrize', 1);W = computePointWeight(pts, type, rings, options);
n = size(W,1);if symmetrize==1 && normalize==0L = diag(sum(W,2)) - W;
elseif symmetrize==1 && normalize==1L = speye(n) - diag(sum(W,2).^(-1/2)) * W * diag(sum(W,2).^(-1/2));
elseif symmetrize==0 && normalize==1L = speye(n) - diag(sum(W,2).^(-1)) * W;
elseerror('Does not work with symmetrize=0 and normalize=0');    
end

computePointCloudRing.m

function ring = computePointCloudRing(pts, k, index)
%计算点云中的环npts = size(pts,1);     %获取点数
ring = cell(npts,1);    %存储环if nargin < 3 || isempty(index)kdtree = KDTreeSearcher(pts);index = knnsearch(kdtree,pts,'K',k);
endfor i = 1:npts  neighbor = pts(index(i,:),:);       %邻近点coefs = pca(neighbor, 'Economy', false);    %使用PCA算法计算局部的特征向量x = [neighbor * coefs(:, 1), neighbor * coefs(:, 2)];       %使用两个主方向构建平面，并将点数据投影到该平面TRI = delaunayn(x);         %构建局部三角网[row,~] = find(TRI == 1);temp = TRI(row,:);      %找寻与该点相关的点temp = sort(temp,2);    %每行按照升序进行排序temp = temp(:,2:end);x=temp(:);x=sort(x);      %对边界点进行排序d=diff([x;max(x)+1]);   %计算相邻元素之差count = diff(find([1;d]));y =[x(find(d)) count];n_sorted_index = size(y,1);start = find(count==1);     %找到连续的索引if ~isempty(start)want_to_find = y(start(1),1);elsewant_to_find = temp(1,1);n_sorted_index = n_sorted_index+1;end%对边界索引进行排序j = 0;    sorted_index = zeros(1,n_sorted_index);while j < n_sorted_indexj = j+1;sorted_index(j) = want_to_find;[row,col] = find(temp == want_to_find);     %找到都有那个边与该点相连接if ~isempty(col)if col(1) == 1      %判断是否为第一列want_to_find = temp(row(1),2);temp(row(1),2) = -1;elsewant_to_find = temp(row(1),1);temp(row(1),1) = -1;end    endendneighbor_index = index(i,sorted_index);ring{i} = neighbor_index;
endend

getoptions.m

function v = getoptions(options, name, v, mendatory)
if nargin<4mendatory = 0;
endif isfield(options, name)v = eval(['options.' name ';']);
elseif mendatoryerror(['You have to provide options.' name '.']);
end

farthestSamplingBySphere.m

function [samplePoint,corresp] = farthestSamplingBySphere(pts,radius)%% **********参数设置************
SHOW_SAMPLING_PROGRESS = true;
SHOW_RESULTS = true;%% **********采样过程************
if SHOW_SAMPLING_PROGRESS || SHOW_RESULTSclose all;figure(1); movegui('northwest');set(gcf,'color','white');hold on;plot3( pts(:,1), pts(:,2), pts(:,3), '.r', 'markersize', 1);axis off; axis equal;set(gcf,'Renderer','OpenGL');
endtic
kdtree = KDTreeSearcher(pts);
samplePoint = [];
corresp = zeros(length(pts), 1);
mindst = nan(length(pts), 1);for k=1:length(pts)if corresp(k)~=0, continue, end%根据距离查询所有点mindst(k) = inf;% 初始化优先队列while ~all(corresp~=0)[~, maxIdx] = max( mindst );if mindst(maxIdx) == 0breakend[nIdxs, nDsts] = rangesearch( kdtree,pts(maxIdx,:), radius );nIdxs = nIdxs{1};nDsts = nDsts{1};% 如果邻近点都被标记，则跳过if all( corresp(nIdxs) ~= 0 )mindst(maxIdx) = 0; continue;end% 新建节点，更新距离samplePoint(end+1,:) = pts(maxIdx,:);for i=1:length(nIdxs)if mindst(nIdxs(i))>nDsts(i) || isnan(mindst(nIdxs(i)))mindst(nIdxs(i)) = nDsts(i);corresp(nIdxs(i)) = size(samplePoint,1);endendif SHOW_SAMPLING_PROGRESS == truefigure(1); plot3( pts(maxIdx,1), pts(maxIdx,2), pts(maxIdx,3), '*g');endend
end
tocend

（二）新生叶器官分割

本研究针对苗期棉株顶端新生叶点云骨架提取困难导致的器官分割过分割问题，提出基于距离场的Quickshift++分割方法。具体步骤如下：

1、新生叶器官末端点云定位
构建闵可夫斯基距离场：在三维坐标系中，首先设定一个称为基点的参考点。这个基点被确定为整个点云集合的质心，即所有点坐标的平均值。为了确保该基点与点云中已有的任何点都不重合，会对其坐标施加一个微小的随机偏移。随后，计算点云中每一个点到这个基点的闵可夫斯基距离。这是一种广义的距离度量方式，通过一个不小于1.0的指数参数来控制距离的计算方式，其数值越大，对距离差异的放大效果就越显著。接下来，基于计算出的距离值，构建一个类似距离场的空间分布。在此分布中，距离值越高的点，其位置越可能是器官的尖端。通过寻找该距离场中的局部极值区域，可以初步识别出这些尖端候选点。最后，采用一种基于密度的快速聚类算法对这些高距离值的点进行分组。该算法能将彼此临近的高密度点聚集起来，形成多个独立的簇，每个簇的核心即代表一个潜在的器官尖端位置。

2、 茎点云分割

（1）局部几何特征的计算与茎叶区分：对于通过聚类得到的每一个候选尖端簇，需要分析其局部区域的几何形态特征。具体方法是，对簇内每个点周围的局部点云进行主成分分析，获取描述其分布形状的三个特征值。通过一个基于这些特征值的综合指标公式，可以量化该簇区域的线性程度。计算所有簇的这个指标值，其中数值最大的簇被认为具有最显著的线性结构，从而被识别为代表茎的区域；而其余指标值较低的簇则被判定为叶的区域。

（2）生长方向的估算与坐标系对齐：首先，分别计算被识别为茎的簇和所有叶簇的三维坐标中位数点。以茎的中位数点为参考起点，指向各个叶簇中位数点的方向向量被用于估算大致的生长方向。对这些方向向量进行统计处理，取其代表性方向（如中位数方向）作为整体的生长方向向量。随后，将整个点云坐标系统进行旋转，使得估算出的生长方向与三维坐标系的Z轴正方向对齐。经过这番变换后，点的Z坐标值便可直接用于判断其高度信息。

（3）茎点云的迭代生长与分割：从茎区域的一个初始种子点开始，进行迭代生长以分割出完整的茎点云。在每一次迭代中，算法会以当前种子点为中心，在一个设定的球形半径范围内，将其中的点归属到茎区域中。同时，生长方向会根据当前已分割的点云进行微调校正。结合校正后的生长方向和设定的步长，确定下一次迭代的新种子点位置。这个生长过程会持续进行，直到新种子点的Z坐标（即高度）超过一个根据当前已分割茎点云高度计算得出的阈值，此时迭代终止，完成了对茎点云的分割。

    3、新生叶片分割

    （1）叶片尖端定位：提取剩余点云中距离值较高的局部极大值区域，作为叶片尖端候选。

    （2）Quickshift++聚类分割：对叶片尖端点云进行密度聚类，形成独立的叶片簇核。

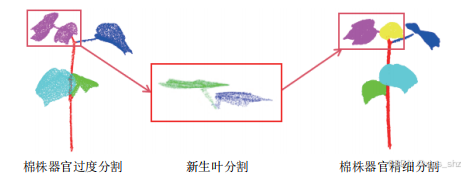
    （3）精细分割与替换：将分割后的叶片点云替换原始过分割区域，实现棉株器官的精确分离（图4）。

            该方法通过结合全局距离场与局部几何特征，有效解决了新生叶点云分割中的过度分割问题，显著提升了苗期棉株器官分割的精度。

    图 4 植株精细分割

    五、结论

    本研究通过整合拉普拉斯骨架提取算法与基于距离场的Quickshift++器官分割方法，实现了对苗期棉株顶端新生叶的精确分割。具体流程如下：

    1. 骨架提取与初步分割
      首先采用拉普拉斯骨架提取算法生成棉株点云骨架，通过骨架顶点分类（根顶点、连接顶点、分支顶点）与方向向量夹角分析，将骨架分解为茎子骨架与叶片子骨架。其中，茎根顶点通过方向向量夹角均值大于π/2的特征被识别，并作为茎子骨架的起点。

    2. 新生叶精细分割
      针对顶端新生叶因未完全展开导致的骨架提取失败问题，引入基于距离场的Quickshift++算法：

      • 距离场构建：通过计算点云到基点的闵可夫斯基距离，生成全局距离场，定位新生叶器官尖端的高距离区域。
      • 密度聚类：利用Quickshift++算法对高距离区域进行聚类，形成簇核，并通过局部几何特征（主成分分析）区分茎与叶片区域（茎区域呈现强线性特征，f(Am)值最大）。
      • 生长方向校正：基于茎簇核与叶簇核的中位数坐标，估算新生叶生长方向，并通过坐标变换将生长方向与Z轴对齐，辅助茎点云的迭代分割。
      • 叶片分割：对剩余点云进行二次Quickshift++聚类，实现叶片区域的精细分割，并替换原始过分割部分。

    3. 表型参数提取
      基于分割后的器官点云，提取茎高、叶长、叶宽、叶面积4个关键表型参数。其中，茎高通过茎子骨架的最长路径计算，叶长与叶宽通过叶片点云的边界框投影获取，叶面积采用三角面片化方法估算。

    该方法通过结合全局拓扑结构分析与局部几何特征，有效解决了苗期棉株顶端新生叶的过度分割问题，显著提升了器官分割精度与表型参数提取的可靠性。

    http://www.dtcms.com/a/356639.html

    相关文章：

  • GPT-Realtime架构与Token成本控制深度解析
  • Linux/UNIX系统编程手册笔记：基本概念
  • Redis面试题--介绍下Redis几种集群模式
  • Shell 秘典（卷二）——号令延展秘术 与 流程掌控心法・if 天机判语篇精解
  • 力扣p1011在D天送达包裹的能力 详解
  • docker-相关笔记
  • 网站加载慢，linux服务器接口请求响应变慢，怎么排查，一般是什么原因
  • 【算法】78.子集--通俗讲解
  • 开源网盘聚合工具Alist：统一管理20+云存储的技术实践
  • vue常见的指令都有哪些,有什么作用
  • 内存页和TLB缓存
  • 计算机专业考研备考建议
  • 前端缓存问题详解
  • CollageIt：简单易用的照片拼贴工具
  • 代理IP服务器平台推荐，企业级动态住宅IP资源哪里找？
  • 在做题中学习（93）：最长公共子序列的长度
  • 1.6 GPU Usage简介
  • 算法题打卡力扣第1004. 最大连续1的个数 III（mid）
  • useEffect用法
  • Git 版本管理核心实践与问题解决手册
  • 群晖Nas上使用工具rsync工具usb同步数据
  • 计算机视觉与深度学习 ｜ 视觉里程计技术全景解析：从原理到前沿应用
  • cloudflare-ddns
  • 过滤器和拦截器的区别？
  • 企业内网与互联网网络安全改造升级深度解析
  • Elasticsearch AI 语义搜索（semantic_text）
  • eslasticsearch+ik分词器+kibana
  • Linux系统部署：Certbot 实现 Nginx 自动续期部署 Let‘s Encrypt 免费 SSL 证书
  • matlab矩阵生成stl格式文件，适用于多孔介质图形生成
  • IAR工程如何生成compile_commands.json文件（能生成但是clangd不能生成“.cache文件”）