第八篇 永磁同步电机控制-MTPA、MTPV
永磁同步电机控制系列课程:
第一篇 永磁同步电机控制-认识电机
第二篇 永磁同步电机控制-电机的分类
第三篇 永磁同步电机控制-硬件基础知识
第四篇 永磁同步电机控制-软件基础知识
第五篇 永磁同步电机控制-数学模型
第六篇 永磁同步电机控制-控制方法
第七篇 永磁同步电机控制-磁场定向控制FOC
第八篇 永磁同步电机控制-MTPA、MTPV
第九篇 永磁同步电机控制-弱磁控制
第十篇 永磁同步电机控制-SVPWM
第十一篇 永磁同步电机控制-位置环、转速环、电流环PI控制
第十二篇 永磁同步电机控制-PI整定
第十三篇 永磁同步电机控制-死区补偿
第十四篇 永磁同步电机控制-大总结
———————————————————————————————————————————
一、什么是MTPA?
MTPA 的全称是 Maximum Torque Per Ampere,即 最大转矩电流比控制。
核心思想:在输出特定转矩时,通过控制定子电流的幅值和相位(即d轴和q轴电流的分量),使得所需要的定子电流幅值最小。
通俗理解:就是用“最省电”的方式产生所需要的力矩。就像开车时,找到一个最合适的油门和档位配合,使得在输出相同动力时,油耗最低。
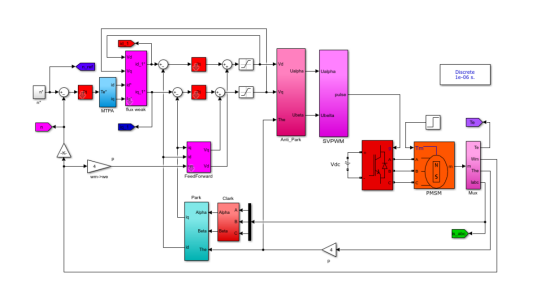
二、为什么需要MTPA?
这主要是由PMSM的转矩产生机理决定的。PMSM的转矩主要由两部分组成:
永磁转矩 (Magnetic Torque):由永磁体磁场与定子电流磁场相互作用产生。这是主要转矩来源。
磁阻转矩 (Reluctance Torque):由于电机转子设计的凸极性(d轴和q轴电感不相等,Ld ≠ Lq),磁路磁阻不同而产生的转矩。
PMSM的总转矩方程可以表示为:
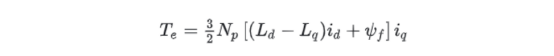
其中:
T_e:电磁转矩;Np:电机极对数;ψ_f:永磁体磁链(常数);
L_d:直轴(d轴)电感; L_q:交轴(q轴)电感;
i_d:直轴(d轴)电流分量;i_q:交轴(q轴)电流分量。
关键点:
如果只是简单地让所有电流都用于产生转矩(即令 i_d = 0),我们只利用了永磁转矩,而浪费了磁阻转矩。这被称为 i_d=0 控制。
对于隐极电机(Surface-Mounted PMSM, SPMSM),通常 L_d = L_q,所以磁阻转矩为0。i_d=0 控制本身就是MTPA控制。
但对于凸极电机(Interior PMSM, IPMSM),通常 L_d < L_q。通过巧妙地注入一个负的i_d电流( demagnetizing current,去磁电流),虽然它本身不直接产生正转矩,但可以显著改变磁阻转矩的大小,使得在总电流 I_s = sqrt{i_d^2 + i_q^2} 不变的情况下,总转矩T_e 变得更大。
因此,MTPA的核心目的就是:对于凸极永磁同步电机(IPMSM),通过优化i_d和i_q的分配,充分利用磁阻转矩,从而实现用最小的电流产生最大的转矩,提高系统的运行效率。
三、MTPA的控制原理
从转矩方程出发,我们的目标是寻找在特定转矩 T_e 下,使定子电流幅值 I_s 最小的 (i_d, i_q) 组合。
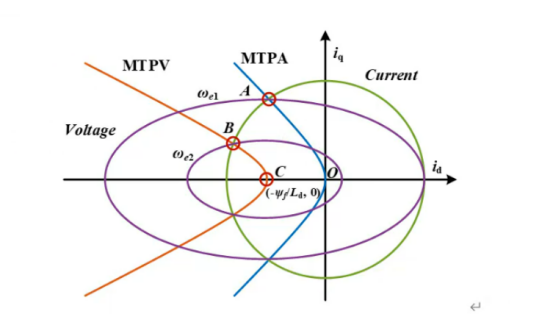
这是一个条件极值问题,可以通过建立拉格朗日函数求解,最终得到MTPA的约束条件关系式:
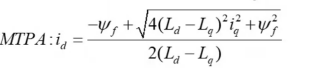
(注意:由于 L_q > L_d,所以 i_d 为负值)
这个公式表明了在MTPA控制下,i_d 和 i_q 不是独立的,它们必须遵循这个关系。给定一个转矩指令(对应一个 i_q 指令),就可以计算出一个最优的 i_d 指令。
在实际系统中,这条 i_d 和 i_q 的关系曲线会被预先计算好,并做成查表法(Look-up Table, LUT) 存储在控制器中,或者通过公式计算法在线实时计算。
四、MTPA的实现方法

公式整理:
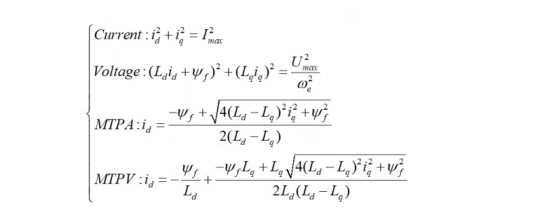



总结与对比
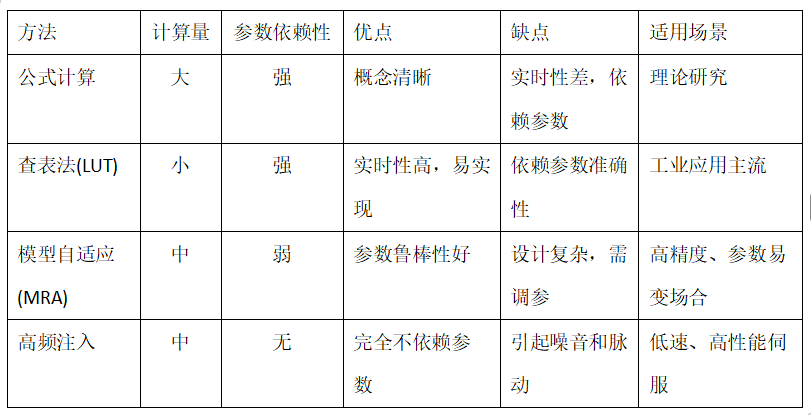
五、MTPA的查表法具体实现
我们来深入讲解永磁同步电机(PMSM)MTPA控制中查表法(Look-Up Table, LUT) 的具体实现步骤。这是一个从理论到实践的完整过程。
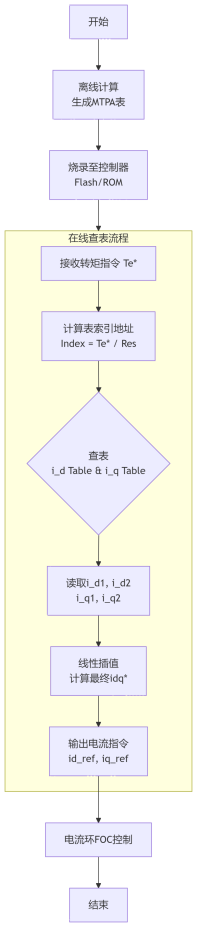
第一阶段:离线制表(Offline Table Generation)
这一步通常在电脑上完成(如使用MATLAB、Python等工具),生成表格后将其烧录到控制器的Flash或ROM中。
步骤 1:确定电机参数
首先,你需要精确知道以下电机参数(通过 datasheet 或电机参数辨识得到):
Psi_f:永磁体磁链 (Wb)
L_d:直轴电感 (H)
L_q:交轴电感 (H)
p:极对数
I_max:电机最大允许电流 (A)
T_max:电机最大所需转矩 (Nm)
步骤 2:选择自变量(索引)
你需要决定用什么作为查表的“索引”(Index)。最常见的有两种:
转矩指令 T_e:直接,但表格需要覆盖整个转矩范围。
电流幅值 I_s:间接,因为MTPA本身就是 I_s 的函数。
这里以转矩指令 T_e 作为索引为例。
步骤 3:创建转矩序列
生成一个从 0 到 T_max(或稍大一点)的转矩指令数组,数组长度决定表的精度。例如:
Te_vector = [0, 0.1, 0.2, 0.3, ..., T_max] (Nm)
步骤 4:为每个转矩点计算最优 (i_d, i_q)
对于 Te_vector 中的每一个转矩值 T_e,求解以下方程组:
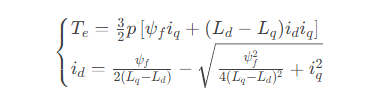
这是一个关于 i_d 和 i_q 的二元方程组。求解方法:
数值求解(常用):将第二个方程代入第一个方程,得到只关于 i_q 的方程,然后使用牛顿-拉夫逊(Newton-Raphson) 等迭代法求解。
解析法:也可以推导出解析解,但形式较复杂。
MATLAB代码示例:
% 给定电机参数
Psi_f = 0.05; % Wb
L_d = 0.5e-3; % H
L_q = 1.0e-3; % H
p = 4;
T_max = 10; % Nm
NumPoints = 100; % 表的大小
Te_vector = linspace(0, T_max, NumPoints);
% 预分配内存
id_table = zeros(1, NumPoints);
iq_table = zeros(1, NumPoints);
for i = 1:length(Te_vector)
T_e = Te_vector(i);
% 使用fzero求解关于iq的方程
fun = @(i_q) (3/2)*p * ( Psi_f * i_q + (L_d - L_q) * ...
( (Psi_f/(2*(L_q-L_d))) - sqrt( (Psi_f^2)/(4*(L_q-L_d)^2) + i_q^2 ) ) .* i_q ) - T_e;
i_q_guess = T_e / ((3/2)*p*Psi_f); % 用id=0控制猜测初值
i_q_sol = fzero(fun, i_q_guess);
% 代入求出对应的id
i_d_sol = (Psi_f/(2*(L_q-L_d))) - sqrt( (Psi_f^2)/(4*(L_q-L_d)^2) + i_q_sol^2 );
% 存储到表中
iq_table(i) = i_q_sol;
id_table(i) = i_d_sol;
end
步骤 5:处理和存储表格
检查计算出的 id_table 和 iq_table 是否超过电机允许的电流限值 I_max。如果超过,需要进行限幅处理。
将最终的 Te_vector(索引)、id_table、iq_table 以数组的形式存储起来。通常存储为C语言风格的数组,方便嵌入代码。
第二阶段:在线查表(Online Look-Up)
这一步在电机控制器的中断服务程序(如电流环中断)中实时执行。
步骤 1:获取指令
获取速度或转矩环给出的转矩指令 T_e_ref。
步骤 2:计算索引地址
根据 T_e_ref 和表格的存储信息,计算其在表中的位置。
Table_Min:表中最小的转矩值(通常是0)。
Table_Max:表中最大的转矩值(T_max)。
Table_Resolution:表的分辨率,Res = (Table_Max - Table_Min) / (Number_of_Points - 1)。
Index:计算出的位置,通常是一个浮点数。
Index = (T_e_ref - Table_Min) / Res
步骤 3:读取表格值
Index 通常不是整数,其整数部分 i = floor(Index) 和小数部分 frac = Index - i 指明了需要插值的位置。
从表中读出 i 和 i+1 位置的值:
id0 = id_table[i]
id1 = id_table[i+1]
iq0 = iq_table[i]
iq1 = iq_table[i+1]
步骤 4:线性插值(Linear Interpolation)
为了获得更平滑、精确的指令,必须在两点之间进行插值。
步骤 5:输出指令
将插值后得到的 i_d_ref 和 i_q_ref 作为电流环的给定值,完成FOC控制。
C语言示例:
// 1. 离线生成的表(存储在Flash中)
const float Te_table[100] = {0, 0.101, 0.202, ...}; // 索引表
const float id_table[100] = {0, -0.5, -1.0, ...}; // d轴电流表
const float iq_table[100] = {0, 2.0, 4.0, ...}; // q轴电流表
const int TABLE_SIZE = 100;
const float TABLE_MIN = 0.0f;
const float TABLE_MAX = 10.0f;
const float TABLE_RES = (TABLE_MAX - TABLE_MIN) / (TABLE_SIZE - 1);
// 2. 在线查表函数
void MTPA_Table_Lookup(float Te_ref, float *id_ref, float *iq_ref)
{
// a. 限幅
if (Te_ref > TABLE_MAX) Te_ref = TABLE_MAX;
if (Te_ref < TABLE_MIN) Te_ref = TABLE_MIN;
// b. 计算索引地址
float Index_f = (Te_ref - TABLE_MIN) / TABLE_RES;
int index = (int)Index_f; // 整数部分
float frac = Index_f - index; // 小数部分
// 防止数组越界
if (index >= TABLE_SIZE - 1)
{
index = TABLE_SIZE - 2;
frac = 1.0f;
}
// c. 查表
float id0 = id_table[index];
float id1 = id_table[index+1];
float iq0 = iq_table[index];
float iq1 = iq_table[index+1];
// d. 线性插值
*id_ref = id0 + (id1 - id0) * frac;
*iq_ref = iq0 + (iq1 - iq0) * frac;
}
// 3. 在电流中断函数中调用
void Current_Loop_ISR()
{
float Te_command = ...; // 从速度环获取转矩指令
float id_ref, iq_ref;
MTPA_Table_Lookup(Te_command, &id_ref, &iq_ref);
// ... 将id_ref, iq_ref送入电流环的PI控制器 ...
}
总结与注意事项
优点:实时性极高,计算负担小。
关键:表的精度依赖于电机参数的准确性。如果参数变化(尤其是 L_d, L_q 会随电流饱和而变化),表的性能会下降。
优化:
对于需要考虑磁饱和的场合,可以制作3维查表,以 i_d 和 i_q 为输入,输出 L_d 和 L_q,然后再计算MTPA,但这更复杂。
对于正反转,通常只需要一个正转矩表,负转矩指令取对应正值的相反数即可(-Te_command -> -id_ref, -iq_ref)。
在极低转矩指令下,可以切换到 i_d=0 控制以避免计算的不稳定性和噪音。
查表法是工业应用中的绝对主流,因为它完美地平衡了性能要求和实现复杂度。
六、MTPV是什么?
永磁同步电机(PMSM)控制中的另一个高级概念:MTPV(最大转矩电压比控制)。MTPV是MTPA在高速区的自然延伸,是弱磁控制(Flux-Weakening Control) 区域内的一个特殊工作轨迹,对于拓展电机的高速运行范围至关重要。
MTPV 的全称是 Maximum Torque Per Voltage,即 最大转矩电压比控制。
核心思想:在电压极限约束下(即椭圆边界上),通过控制 i_d 和 i_q,使得输出特定转矩时所需要逆变器输出的电压幅值最小。
等价理解:在电压极限约束下(即给定转速和直流母线电压),找到能产生最大可能转矩的 (i_d, i_q) 工作点。
简单来说:MTPA是“省电流”的控制方式,而MTPV是“省电压”或“榨干电压”的控制方式。
1. 为什么需要MTPV?—— 电压极限的挑战
随着电机转速的升高,反电动势(Back-EMF)会成比例增大。电机控制器的直流母线电压是有限的,这导致逆变器能够输出的最大相电压也是一个定值(U_{max})。这个电压极限可以用一个在dq坐标系下的电压方程和不等式来描述:
电压方程:
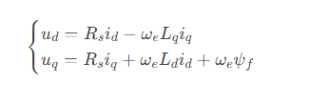
通常忽略定子电阻 R_s(在高速时其压降占比较小),则电压幅值约束为:
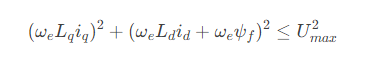
两边同时除以 ωe^2,得到:
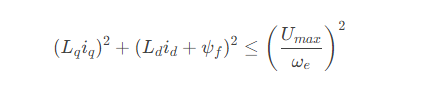
这个不等式在dq电流平面上是一个椭圆,称为电压极限椭圆。

核心问题:
在高速区,电压极限椭圆收缩到MTPA轨迹之内。这意味着,如果继续按MTPA轨迹运行,所需要的电压会超过逆变器能提供的最大电压 U_{max},导致电流环饱和失控。
解决方案:弱磁控制 (Flux-Weakening)
此时,必须注入更大的负的 i_d 电流(去磁电流),进一步削弱电机内部的磁场,从而降低反电动势,使得电机能在更高的转速下运行。这个工作区域就是弱磁区。
而MTPV,就是在弱磁区内,找到一条最优的工作轨迹。
2. MTPV的控制原理与方程
MTPV的数学目标是在电压极限椭圆的边界上(V_s = V_{max}),寻找使转矩 T_e 最大的点。这同样是一个条件极值问题,可以通过拉格朗日乘数法求解。
MTPV的优化条件为:

请注意:
这个公式对于 凸极电机(IPMSM) 有效。
对于 隐极电机(SPMSM),这个公式会发散。隐极电机的MTPV轨迹就是电压椭圆与负id轴的交点。在实际控制中,我们总是选择负id轴上的点来获得最大转矩。
3. MTPV的实现方法
与MTPA类似,MTPV的实现也主要依靠查表法(LUT)。
a) 离线制表
确定参数:需要已知 L_d, L_q, ψ_f。
创建转速序列:生成一个从基速以上到最高转速的数组 Rpm_vector。
计算MTPV轨迹:
对于每个转速 rpm,计算对应的电角速度 w_e。
计算该转速下的电压极限椭圆方程。
联立求解:将 MTPV关系式 和 电压极限椭圆方程 联立,求解出此时椭圆边界上满足MTPV条件的 (i_d, i_q) 点。
记录该点对应的转矩 T_e。
生成表格:创建一个以 转速 或 转矩 为索引,以最优的 (i_d, i_q) 为值的表。
b) 在线查表
控制器实时检测电机转速 rpm 和直流母线电压 U_dc(用于计算 U_{max})。
以当前转速为索引,查询MTPV表,得到对应的 i_d 和 i_q 指令。
将电流指令送入电流环执行。
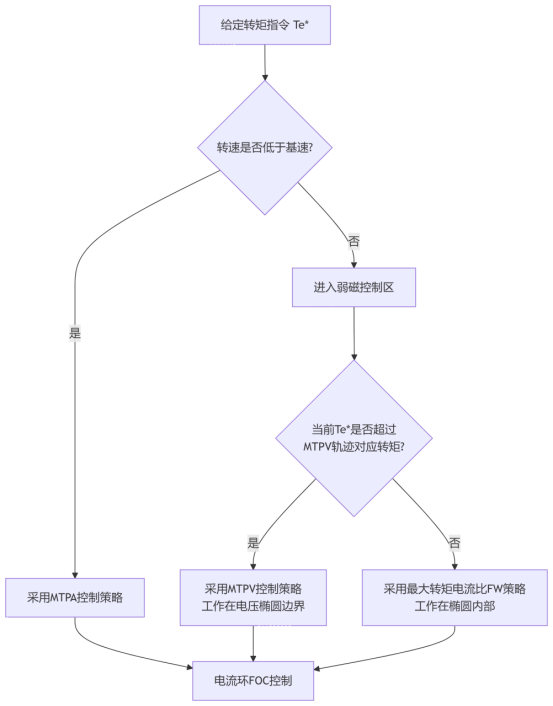
4. MTPV的注意事项与特点
仅适用于IPMSM:MTPV的有效性依赖于电机的凸极性(L_d < L_q)。对于SPMSM,弱磁控制就是沿着负id轴运行。
对参数极度敏感:L_d, L_q, ψ_f 的准确性至关重要,尤其是磁饱和会显著影响这些参数。参数不准会导致计算出的MTPV点偏离真正的最优点。
稳定性问题:在MTPV点附近,电压和电流环的增益需要仔细设计,否则容易产生振荡。
与MTPA的平滑切换:在实际控制器中,必须实现从恒转矩区(MTPA)到弱磁区(包括MTPV)的平滑过渡,避免转矩和电流的突变。
七、 MTPA、MTPV总结
MTPA:用于低速/基速以下区域,目标是最小化电流以产生所需转矩,提高效率。
MTPV:用于高速/深度弱磁区域,目标是最大化利用有限电压以产生最大可能转矩,拓展高速范围。
MTPV是挖掘IPMSM高速性能极限的关键技术,广泛应用于电动汽车、航空航天等对高速性能有苛刻要求的领域。
