C语言————函数递归(通俗易懂)
我们在学习些新的函数时,首先我们得理解它是什么?是怎么定义的?然后去了解他的用途,最后我们自己要会用,知道用在什么地方?什么时候用?用的时候要注意些什么?
有一个条理清晰的学习逻辑,会让我们学习起来事半功倍。
小博在这里带大家从入门到应用,用通俗易懂的文字讲清楚函数递归。
一、递归是什么
递归:简单点说就是函数自己调用自己。可以理解为“俄罗斯套娃”,将一个大型的复杂的问题层层转化为和原问题相似的规模较小的子问题来求解,直到不能够再拆分为止。
凡事物极必反,递归也一样。递归必须是有条件的,不能够无限递归下去。
递:递推;归:回归。你品,你细品。 🤨🤨
二、递归举例
come on !! 直接上例题:
求n!:
1、用数学公式求n!
当我没有学过递归时,我脑子里根本想不到用其他的方法,只能根据数学公式,去解决这个问题。
即n!=n*(n-1)*(n-2)*......*2*1。
//用数学公式求n!
#include <stdio.h>
int main()
{int n = 0;int ret = 1;scanf("%d", &n);for (int i = 1; i <= n; i++){ret *= i;}printf("%d", ret);return 0;
}2、用递归的方法求n!
当我学了递归之后,看到这个数学问题是有规律的,即:
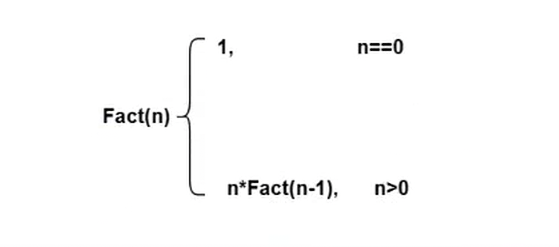
//用递归方法求n!
#include <stdio.h>
int Fact(int n)
{if (n == 0)return 1;elsereturn n * Fact(n - 1); //继续调用Fact(),直到n=1为止
}int main()
{int n = 0;scanf("%d", &n);int ret=Fact(n); //调用函数Fact()printf("%d", ret);return 0;
}3、分析递归过程
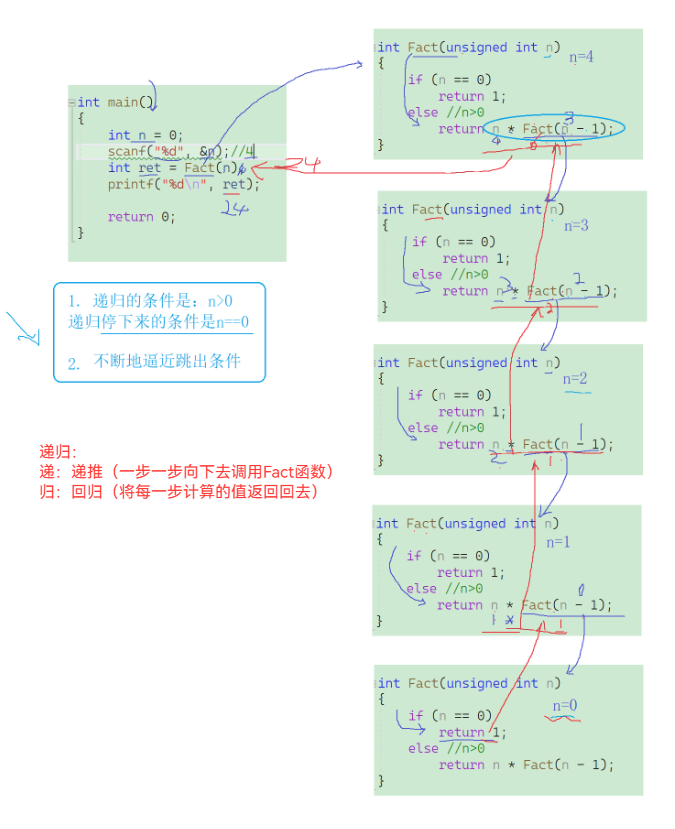
三、递归练习
根据上面的讲解,想必大家对递归也有了初步的了解,下面我来写一道例题,大家可以自行练习一下。
例:输入一个整数m,按照顺序打印整数的每一位。
比如:输入1234 输出1 2 3 4
1、小博分析
我们先进行分析,可以用笔写出分析过程,找出规律,往递归上靠。
小博分析:
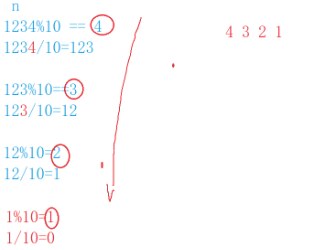
小博刚开始分析时,发现了该过程的规律,但当小博尝试写代码去解决的时候,却写不出对应的代码,完了卡住了 😥😥,你们是不是也经常这样!!
事后,小博对自己的行为进行了反思,发现:首先我并没有捋清楚自己的思路,抱着试一试、感觉会了的态度去写,结果问题没有解决,反而还花费了大量的时间,同时心灵还受到极大的挫败感。所以,我们在写代码时,要先有清晰明了的思路之后再去写。俗话说,磨刀不误砍柴功呢!
回归正题:
按照上面小博的分析,发现是倒着打印出来该数字的,如果想正着打印的话,还需再分析

我们发现一个数的最低位是最容易得到的,要想办法把该数拆开,直到拆成一位就不用再拆了。
2、代码实现
#include <stdio.h>
void print(int m)
{if (m > 9){print(m / 10);}printf("%d ", m % 10);
}int main()
{int m = 0;scanf("%d", &m);print(m); //用来打印m的每一位return 0;
}代码的流程
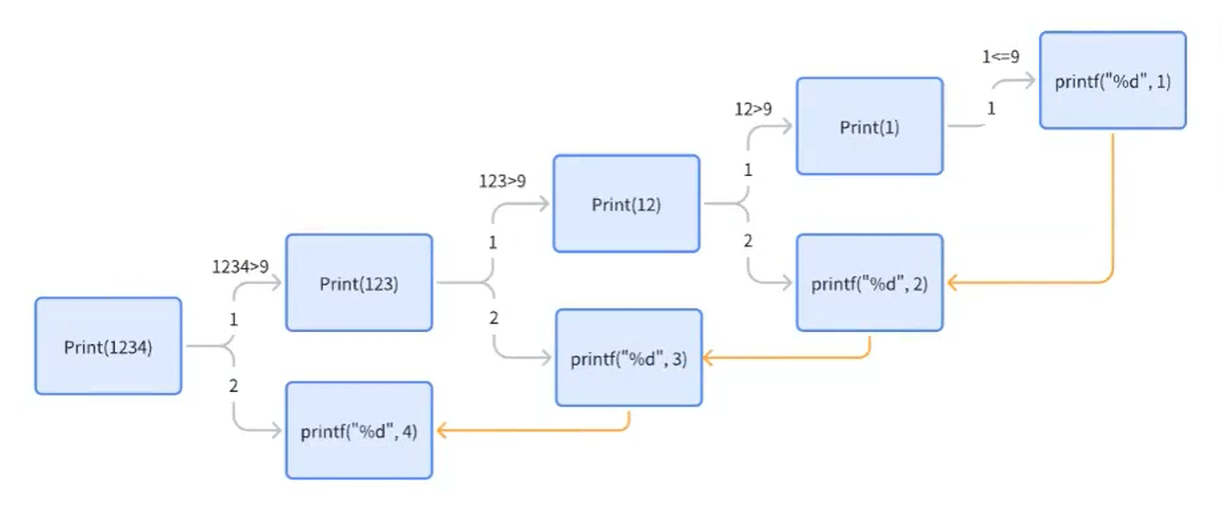
注意:每次调用print()函数时,就会进入该函数,再进入该函数......每一级的print() 都是来自上一步的,然而每次执行完该函数时,都会留下一个printf("%d",m);未被执行,因此执行结束后,还会一步一步返回回归到上层去执行该语句。
此外,使用递归的时候要注意,每次递归函数的调用都会开辟属于自己的栈帧空间,称为运行时堆栈,直到函数递归不再继续,还是回归才逐释放栈帧空间。所以递归太深,就会浪费太多的栈帧空间,也可能会造成栈溢出。
看完上述内容,是否对递归有了更深的理解呢!!然而我们要知道,递归很难想到,也不一定是最优解,但是有的地方会简化代码,让问题简单化。
学习数据结构时,会常用到递归。
好了小博今天就将到这里,欢迎大家留言评论!!
这里小博再送给大家我喜欢的一句话:“与凤凰同飞,必是俊鸟;与虎狼同行,必是猛兽。”
加油!!

