控制系统仿真之时域分析(二)

一、时域分析法

时域分析法是从传递函数出发直接在时域上研究控制系统性能的方法，实质上是研究系统在某典型输入信号下随时间变化的曲线，从而分析系统性能。

控制系统的时域响应决定于系统本身的参数和结构，还有系统的初始状态，以及输入信号的形式。

二、典型信号

典型信号是指很接近实际控制系统经常遇到的输入信号，并在数学描述上加以理想化后能用较为典型且简单的函数形式表达出来的信号。

典型的输入信号的函数形式有阶跃函数、斜坡函数、抛物线函数、脉冲函数及正弦函数。

1、阶跃函数

  

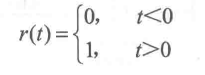
阶跃函数形式的输入信号在实际控制系统中较为常见。例如，速度控制系统，室温控制系统，水位调节系统、某些工作状态突然改变或接收突然增减输入的控制系统（火炮的方位角、俯视角的控制系统），都可以采用阶跃函数形式的信号作为典型输入信号。

2、斜坡函数

实际中输入信号的形式接近于斜坡函数的控制系统，主要有跟踪直线飞行目标（如飞机、通信卫星等）的跟踪系统，以及输入信号随时间逐渐增减变化的控制系统。

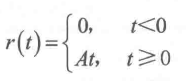
3、抛物线函数

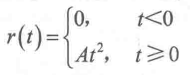
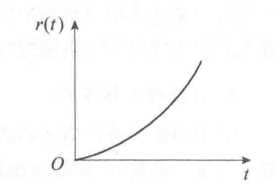
航天飞行器控制系统的输入信号，一般可认为接近等加速度，可以用抛物线函数描述其输入信号。

4、脉冲函数

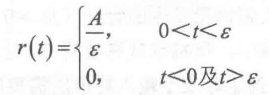
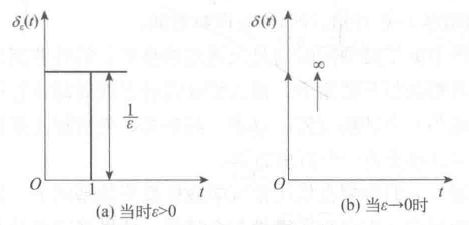
实际中，输入给定控制信号类似脉冲函数的控制系统并不多见，但有些系统的扰动信号类似脉冲函数。

三、时域响应的暂态性能指标

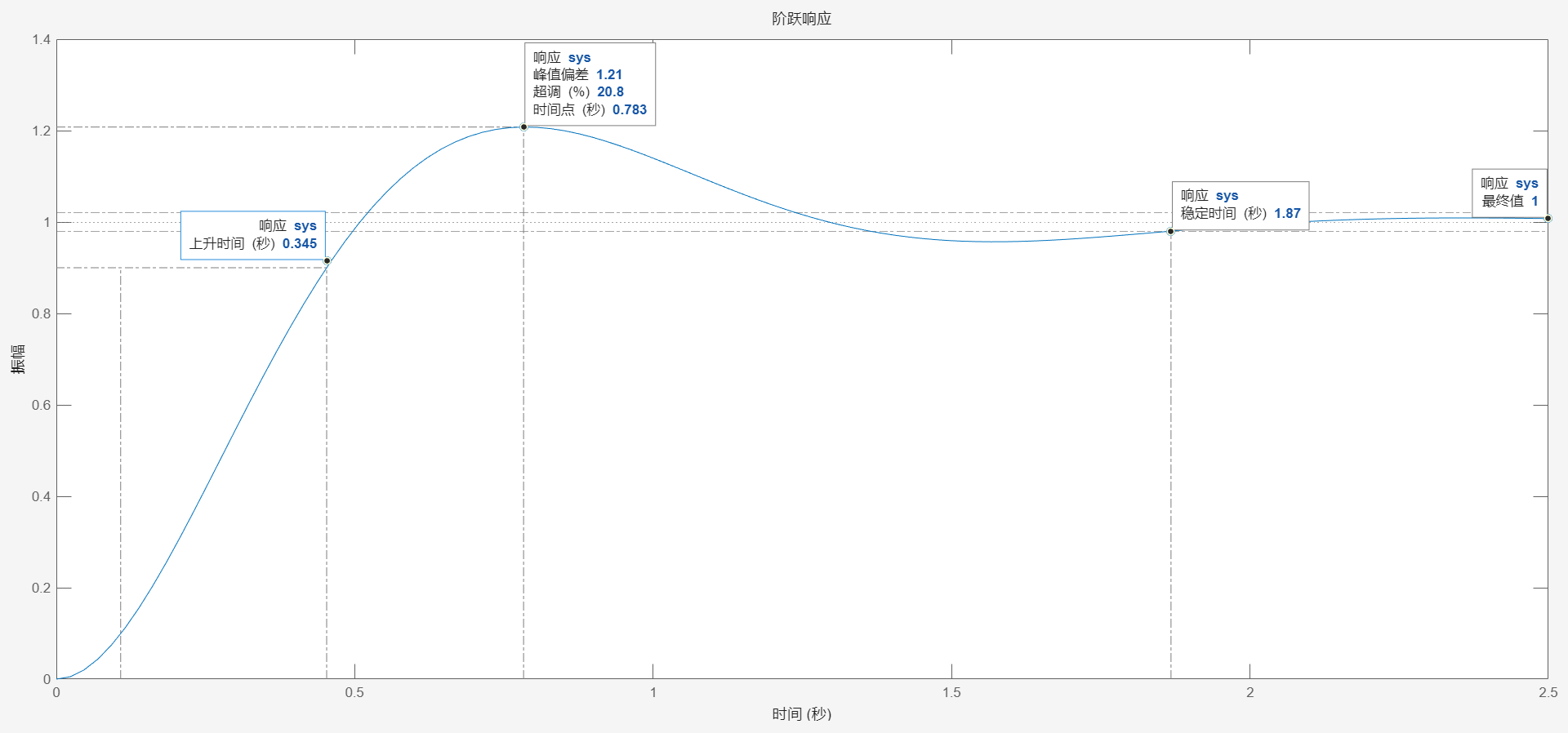
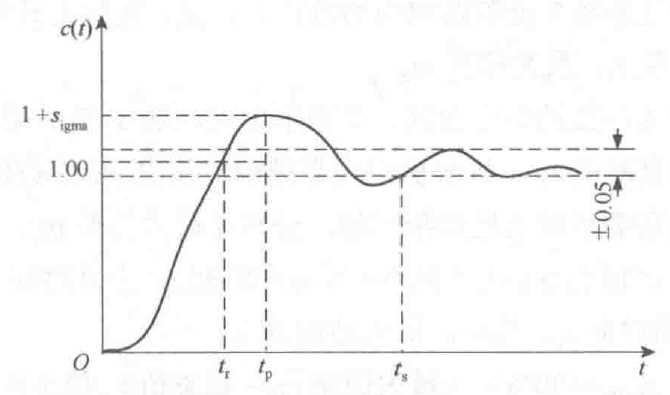
通常采用单位阶跃响应来表征一个系统的暂态性能。用来表述单位阶跃输入暂态响应的典型性能指标有：最大超调量、峰值时间、上升时间和调整时间。

1、最大超调量s：最大超调量规定为在暂态期间输出超过对应输入的终值的最大偏离量。

2、峰值时间tp：对应于最大超调量发生的时间(从t=0开始计时)称为峰值时间。

3、上升时间tr：在暂态过程中，指响应从0.1上升到0.9所需要的时间。振荡系统，第一次到达1所需要的时间。

4、调整时间ts：输出与对应的输入终值之间的偏差达到容许范围(一般取5%或2%)不再出来所经历的暂态过程时间（t=0开始计时）称为调整时间。

控制系统设计必然成为一个试凑过程，寻求一组参量，使所提出来的各性能指标并不能完全满足要求，却是可以接受一个折中的方案。

四、稳态误差

在稳态条件下（对于稳定系统）输入增加后并经过足够长的时间，其暂态响应已经衰减到微不足道时，稳态响应的期望值与实际值之间的误差。

控制系统的稳态误差有两类，即给定稳态误差和扰动稳态误差。

给定稳态误差用来衡量随动系统的稳态性能。对于随动系统，给定的参考输入时变化的，要求响应以一定精度跟随给定的变化而变化，其响应的期望值就是给定的参考输入。

扰动稳态误差用来衡量恒值调节系统的稳态性能。对于恒值调节系统，给定的参考输入不变。