AT_abc406_f [ABC406F] Compare Tree Weights
AT_abc406_f [ABC406F] Compare Tree Weights
洛谷题目传送门
ATcoder题目传送门
题目描述
给定一个有 NNN 个顶点的树 TTT,顶点和边分别编号为顶点 111, 顶点 222, …\ldots…, 顶点 NNN 和边 111, 边 222, …\ldots…, 边 (N−1)(N-1)(N−1)。
特别地,边 iii (1≤i≤N−1)(1 \leq i \leq N-1)(1≤i≤N−1) 连接顶点 UiU_iUi 和顶点 ViV_iVi。
此外,每个顶点都有一个权重,最初,所有顶点的权重都为 111。
给定 QQQ 个查询,请按顺序处理它们。每个查询是以下两种类型之一:
1 x w:将顶点 xxx 的权重增加 www。2 y:如果删除边 yyy,TTT 将分裂成两个子树(连通分量)。将每个子树中包含的顶点的权重总和作为该子树的权重时,输出两个子树权重的差。
关于第二种类型的查询,可以证明,从 TTT 中选择任意一条边并删除它时,TTT 总是会分裂成两个子树。
另外,请注意,第二种类型的查询实际上并没有删除边。
输入格式
输入按以下格式从标准输入给出。
NNN
U1U_1U1 V1V_1V1
U2U_2U2 V2V_2V2
⋮\vdots⋮
UN−1U_{N-1}UN−1 VN−1V_{N-1}VN−1
QQQ
query1\mathrm{query}_1query1
query2\mathrm{query}_2query2
⋮\vdots⋮
queryQ\mathrm{query}_QqueryQ
每个查询 queryi\mathrm{query}_iqueryi (1≤i≤Q)(1 \leq i \leq Q)(1≤i≤Q) 按以下任一格式给出。
111 xxx www
222 yyy
输出格式
设第二种类型查询的个数为 KKK,输出 KKK 行。第 iii 行 (1≤i≤K)(1 \leq i \leq K)(1≤i≤K) 输出第 iii 个第二种类型查询的答案。
输入输出样例 #1
输入 #1
6
1 2
1 3
2 4
4 5
4 6
5
2 1
1 1 3
2 1
1 4 10
2 5
输出 #1
2
1
17
说明/提示
「数据范围」
- 2≤N≤3×1052 \leq N \leq 3 \times 10^52≤N≤3×105
- 1≤Ui,Vi≤N1 \leq U_i, V_i \leq N1≤Ui,Vi≤N
- 1≤Q≤3×1051 \leq Q \leq 3 \times 10^51≤Q≤3×105
- 1≤x≤N1 \leq x \leq N1≤x≤N
- 1≤w≤10001 \leq w \leq 10001≤w≤1000
- 1≤y≤N−11 \leq y \leq N-11≤y≤N−1
- 输入均为整数
- 给定的图是一棵树。
- 至少存在一个第二种类型的查询。
「样例 1 解释」
树 TTT 的结构和顶点编号对应如下图左所示。最初,所有顶点的权重都为 111。
对于第 111 个查询,考虑删除边 111。此时,树会分裂成包含顶点 111 的子树和包含顶点 222 的子树。包含顶点 111 的子树的权重为 222,包含顶点 222 的子树的权重为 444,因此输出它们的差 222。(下图右)
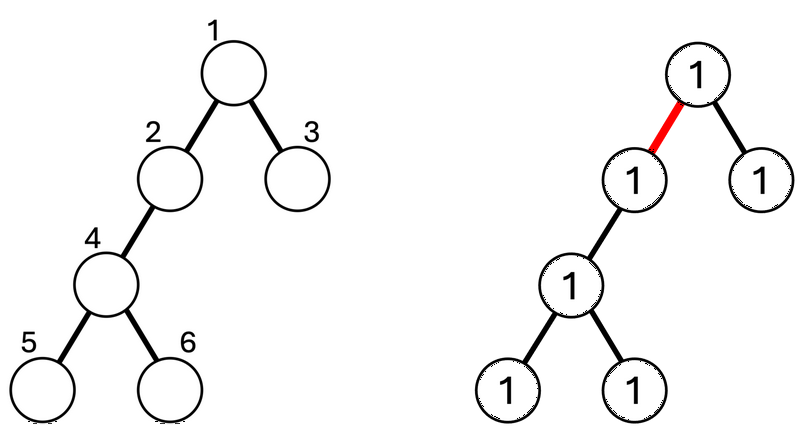
对于第 222 个查询,将顶点 111 的权重增加 333。
对于第 333 个查询,考虑删除边 111。包含顶点 111 的子树的权重为 555,包含顶点 222 的子树的权重为 444,因此输出它们的差 111。(下图左)
对于第 444 个查询,将顶点 444 的权重增加 101010。
对于第 555 个查询,考虑删除边 555。此时,树会分裂成包含顶点 444 的子树和仅包含顶点 666 的子树。包含顶点 444 的子树的权重为 181818,仅包含顶点 666 的子树的权重为 111,因此输出它们的差 171717。(下图右)
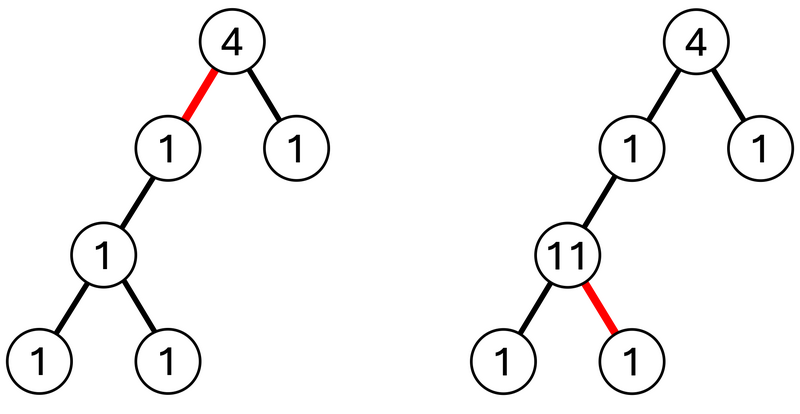
因此,按顺序换行输出第二种类型查询的答案 2,1,172, 1, 172,1,17。
思路详解
题目分析
其实没什么好分析的,又要单点修改,还要求子树内的和,那显然是树链剖分+数据结构,在这里我采用树状数组。
code
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,m;
struct Tree_array{//树状树状int c[N];int lowbit(int x){return x&(-x);}void change(int x,int v){for(;x<=n;x+=lowbit(x))c[x]+=v;}int _sum(int x){int res=0;for(;x;x-=lowbit(x))res+=c[x];return res;}int sum(int x,int y){return _sum(y)-_sum(x-1);}
};
vector<int>e[N];
int siz[N],fa[N],son[N],dep[N];
int id[N],reid[N],top[N],tim=0,mx[N];
int w[N];
class Tree{//树链剖分
private:Tree_array tr;void dfs1(int u,int fath,int dp){//第一次深搜求出fa,siz,son,depsiz[u]=1;fa[u]=fath;dep[u]=dp;for(int v:e[u]){if(v==fath)continue;dfs1(v,u,dp+1);siz[u]+=siz[v];if(siz[v]>siz[son[u]])son[u]=v;}}void dfs2(int u,int fath,int ori){//第二次深搜求出id,reid,topid[u]=++tim;reid[tim]=u;top[u]=ori;mx[u]=id[u];if(son[u]){//从这里也可以看出一个子树内id是连续的dfs2(son[u],u,ori);mx[u]=max(mx[u],mx[son[u]]);}for(int v:e[u]){if(v==fath||v==son[u])continue;dfs2(v,u,v);mx[u]=max(mx[u],mx[v]);}}
public:void build(){//建树dfs1(1,0,1);dfs2(1,0,1);for(int i=1;i<=n;i++)tr.change(id[i],w[i]);}void add(int u,int v){tr.change(id[u],v);}//将节点u的权值加vvoid print(){for(int i=1;i<=n;i++)cout<<reid[i]<<' '<<tr.sum(i,i)<<'\n';}int query(int u){//求u的子树中的权值和int res=tr.sum(id[u],mx[u]);return res;}
}tr;
struct node{int x,y;
}a[N];
int main(){
//由于要在树上求子树和,而且要单点修改,那显然是树链剖分+数据结构,在这里我使用树状数组
//由于在一个子树中标记是连续的,所以我们开一个mx记录在这个子树中标记最大的即可ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n-1;i++){int x,y;cin>>x>>y;e[x].push_back(y);e[y].push_back(x);a[i]={x,y};}for(int i=1;i<=n;i++)w[i]=1;tr.build();int q;cin>>q;for(int i=1;i<=q;i++){int op,x,y;cin>>op>>x;if(op==1){cin>>y;tr.add(x,y);}else{auto [qx,qy]=a[x];if(dep[qx]<dep[qy])swap(qx,qy);cout<<abs(tr.query(1)-tr.query(qx)*2)<<'\n';
//总和减去当前这颗数的和即为剩余的和,所以要减2次}}return 0;
}
