当前位置：首页 > news >正文

力扣（滑动窗口最大值）

news 2025/8/27 12:21:15

解析 LeetCode 239. 滑动窗口最大值：双端队列的巧妙运用

一、题目分析

在这里插入图片描述

（一）问题定义

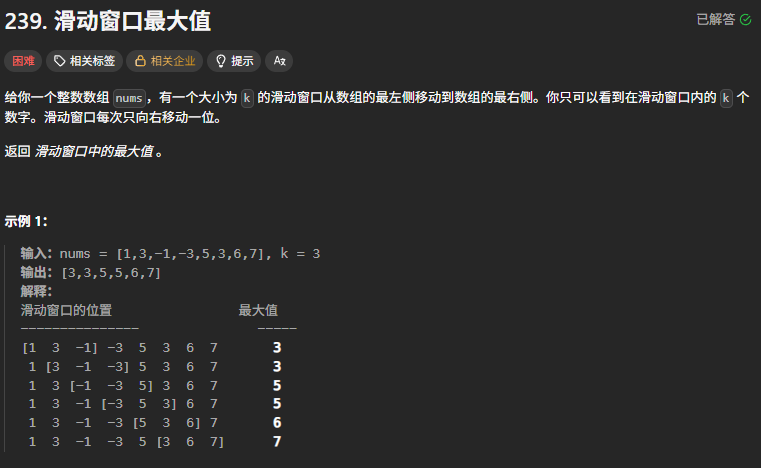
给定整数数组 nums 和滑动窗口大小 k，窗口从数组最左侧滑动到最右侧，返回每个窗口中的最大值。例如，nums = [1,3,-1,-3,5,3,6,7], k = 3 时，需返回 [3,3,5,5,6,7] 。

（二）核心挑战

效率要求：若直接对每个窗口遍历找最大值，时间复杂度为 $\times k)$ （n 是数组长度），当 n 较大时会超时。
数据结构适配：需找到一种数据结构，能动态维护窗口内的最大值候选，支持快速添加新元素、移除过期元素、获取当前最大值。

二、算法思想：双端队列维护单调递减序列

（一）核心思路

利用双端队列存储窗口内元素的索引，且保证队列中索引对应的数组值单调递减。这样，队首元素始终是当前窗口的最大值索引。具体逻辑：

移除过期元素：窗口右移时，若队首索引超出窗口左边界（i - k + 1 ），则移除队首。
维护单调递减：遍历到新元素时，移除队列中所有对应值小于当前元素的值的索引（因为它们不可能成为后续窗口的最大值），再将当前索引加入队列。
记录最大值：当窗口形成（i >= k - 1 ）时，队首索引对应的值即为当前窗口最大值，存入结果数组。

（二）双端队列的优势

两端操作高效：支持从队首移除过期元素，从队尾移除较小值的索引，均为 $O (1)$ 操作。
维护单调序列：确保队列中始终是当前窗口内可能成为最大值的候选，队首即为最大值。

三、代码实现与详细解析

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {// 处理特殊情况：数组为空或窗口大小不合法if (nums == null || nums.length == 0 || k <= 0) {return new int[0];}int n = nums.length;// 结果数组长度为 n - k + 1int[] result = new int[n - k + 1];int index = 0;// 双端队列存储索引，保持对应数值单调递减Deque<Integer> deque = new LinkedList<>();for (int i = 0; i < n; i++) {// 1. 移除队首超出窗口左边界的索引（窗口左边界：i - k + 1）while (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {deque.pollFirst();}// 2. 移除队列中所有对应值小于当前元素的索引（保证单调递减）while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {deque.pollLast();}// 3. 当前元素索引加入队列尾部deque.offerLast(i);// 4. 当窗口形成（i >= k - 1），记录当前窗口最大值（队首索引对应的值）if (i >= k - 1) {result[index++] = nums[deque.peekFirst()];}}return result;}
}

（一）代码流程拆解

特殊情况处理：若数组为空、长度为 0 或窗口大小 k 不合法，直接返回空数组。
初始化变量：result 存储结果，长度为 n - k + 1；deque 作为双端队列，存储元素索引。
遍历数组：
- 移除过期索引：若队首索引小于窗口左边界（i - k + 1 ），说明该索引对应的元素已不在当前窗口，移除队首。
- 维护单调递减：从队尾开始，移除所有对应值小于当前元素的索引（这些索引对应的元素不可能成为后续窗口的最大值），再将当前索引加入队尾。
- 记录最大值：当 i >= k - 1 时，窗口已形成，队首索引对应的值是当前窗口最大值，存入 result 。
返回结果：遍历结束后，result 存储所有窗口的最大值，返回即可。

（二）关键逻辑解析

窗口左边界计算：窗口右边界是 i ，左边界为 i - k + 1 ，用于判断队首索引是否过期。
单调递减维护：通过 while 循环移除队尾所有小于当前元素的索引，确保队列中索引对应的数值始终单调递减。例如，当前元素是 5 ，队列中有 3、-1 ，则移除这两个索引，再加入 5 的索引，保证队列单调。
结果记录时机：当 i >= k - 1 时，窗口首次形成（如 k=3 时，i=2 是第一个窗口），之后每次循环都记录当前窗口最大值。