【数据结构】树和二叉树——二叉树

树和二叉树

树的基本概念

树的定义：

• 树（Tree） 是 n (n ≥ 0) 个结点 的有限集。
• 当 n = 0 时，称为空树。
• 对于 n > 0 的树，它必须满足以下条件：
  1. 有一个特殊的结点，称为 根（Root）。
  2. 除根以外的其他结点可分为若干个互不相交的有限集，每个集合本身又是一棵树，称为根的 子树（SubTree）。

简而言之：树是由一个根和若干棵子树组成的层次结构。

基本术语：

1. 结点（Node）
   树中的一个元素，包含一个数据元素以及若干指向子树的分支。
2. 结点的度（Degree of Node）
   结点所拥有的子树个数。
   • 度为 0 的结点叫 叶子结点（Leaf） 或 终端结点。
   • 度不为 0 的结点叫 非终端结点（Non-leaf） 或 分支结点。
3. 树的度（Degree of Tree）
   树中所有结点的度的最大值。
4. 孩子（Child）与双亲（Parent）
   • 结点的子树的根叫该结点的 孩子。
   • 该结点叫孩子的 双亲。
5. 兄弟（Sibling）
   同一个双亲的孩子之间互为兄弟。
6. 祖先（Ancestor）与子孙（Descendant）
   • 从根到某结点路径上的所有结点，都是该结点的 祖先。
   • 某结点的所有子树中的结点，都是该结点的 子孙。
7. 结点的层次（Level）
   • 根为第 1 层，它的孩子为第 2 层，依此类推。
8. 树的深度（Depth）/高度（Height）
   树中结点的最大层次称为 树的深度或高度。
9. 森林（Forest）
   由 m (m ≥ 0) 棵互不相交的树组成的集合。
   • 删除树的根结点后，其子树集合就是一个森林。

        A/ | \B  C  D/ \E   F

• 结点：A, B, C, D, E, F
• 根：A
• 叶子：C, D, E, F
• 度：A 的度是 3，B 的度是 2，其余都是 0
• 树的度：max(3,2,0,0,0,0) = 3
• 层次：A(第 1 层)，B/C/D(第 2 层)，E/F(第 3 层)
• 高度：3
• 删除根 A 后，剩下 {B 子树, C 子树, D 子树} → 森林

树的性质：

1. 性质 1
   树中的结点数 = 所有结点的度数之和 + 1。
   （因为除了根以外，每个结点都有一个入边）
2. 性质 2
   度为 m 的树中，第 i 层上最多有 $m^{i-1}$ 个结点。
3. 性质 3
   高度为 h 的 m 叉树最多有
   $$\frac{m^h-1}{m-1}$$
   个结点（满 m 叉树）。
4. 性质 4
   具有 n 个结点的 m 叉树的最小高度为
   $$\lceil logm(n\cdot (m-1)+1)\rceil$$

二叉树的概念

二叉树的定义：

• 二叉树（Binary Tree） 是 n (n ≥ 0) 个结点的有限集合。
• 特点：
  1. 或者为空树（n=0）；
  2. 或者由一个根结点和两棵互不相交的子树组成，这两棵子树分别称为 左子树 和 右子树，并且二叉树是有序的。

👉 注意：二叉树和度为 2 的树不同

• 度为 2 的树是“最多两个孩子”。
• 二叉树要求 每个结点都有左右次序，即使只有一个孩子，也必须区分是左还是右。

特殊二叉树：

1. 满二叉树（Full Binary Tree）
   • 深度为 h，且有 2h−12h−1 个结点的二叉树。
   • 每一层都填满，没有缺失。

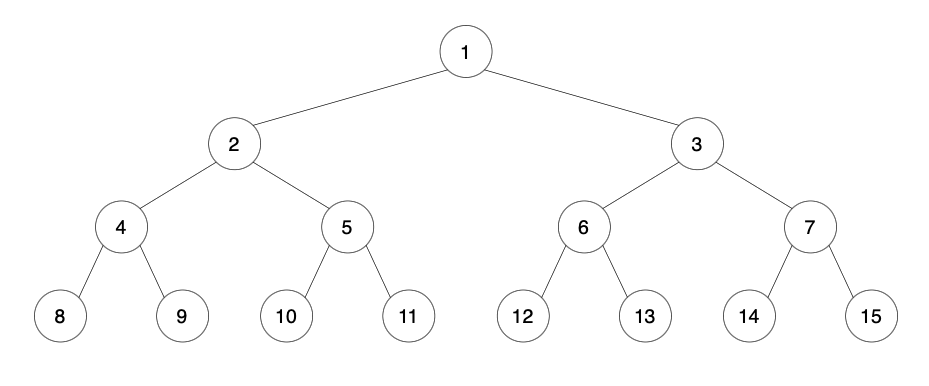
2. 完全二叉树（Complete Binary Tree）

• 深度为 h 的二叉树，若除第 h 层外，其它各层都达到最大结点数，且第 h 层的结点都集中在最左边，则称为完全二叉树。
• 完全二叉树常用顺序存储（数组）非常方便。

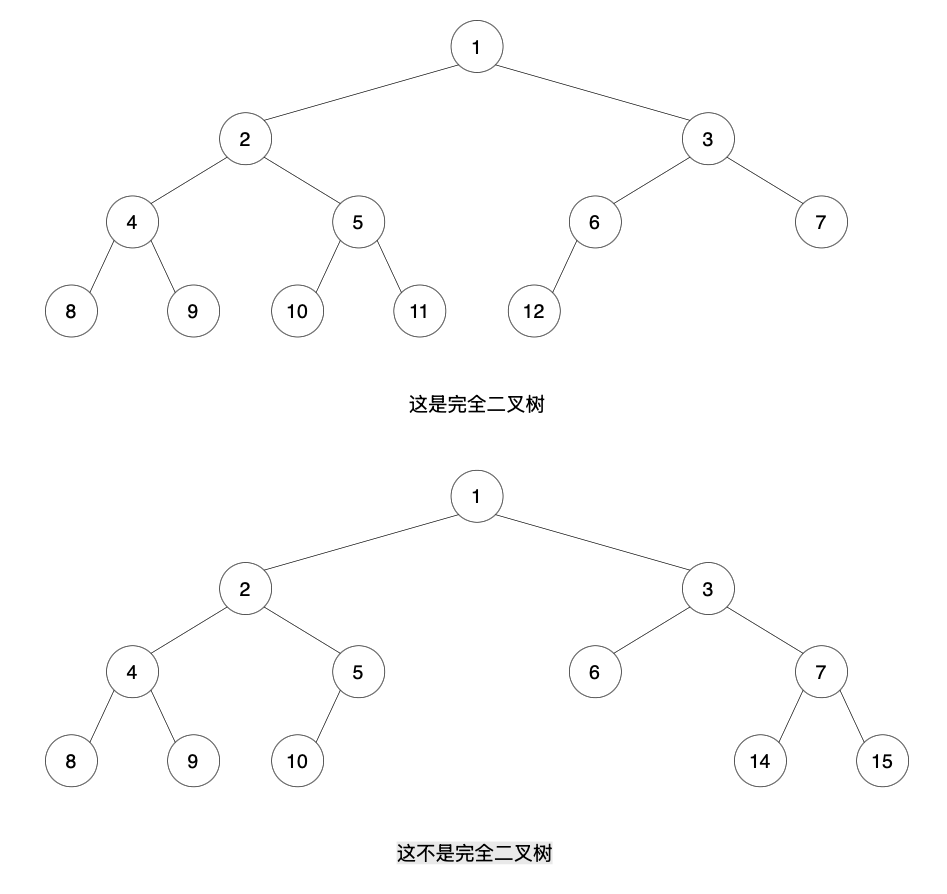
3. 斜树（Skewed Tree）

• 每个结点只有左子树的二叉树称 左斜树。
• 每个结点只有右子树的二叉树称 右斜树。

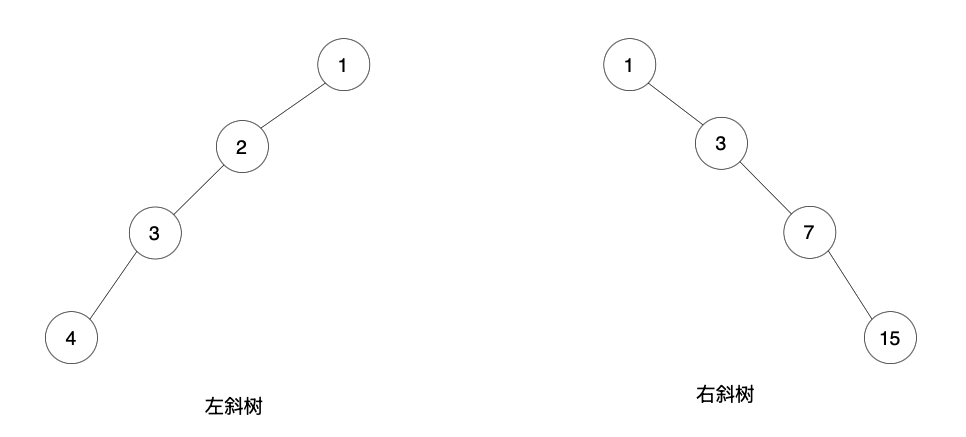
二叉树的性质:

1. 性质 1
   在二叉树的第 $i$ 层上，最多有 $2^{i-1}$ 个结点（$i\ge 1$）。
2. 性质 2
   深度为 $h$ 的二叉树，最多有 $2^h-1$ 个结点（满二叉树情况）。
3. 性质 3
   对任何一棵非空二叉树：
   若叶子结点数为 $n_0$，度为 2 的结点数为 $n_2$，则有：
   $$n_0=n_2+1$$
4. 性质 4（重要，完全二叉树编号性质）
   若对一棵完全二叉树按层序编号：
   • 编号 $i$ 的结点，若$ i > 1$，则其双亲为 $\lfloor i/2\rfloor$；
   • 若 $2i\le n$，则左孩子编号为 $2i$；
   • 若 $2i+1\le n$，则右孩子编号为 $2i+1$。

二叉树的存储结构：

1. 顺序存储（数组）
   • 用数组存储完全二叉树，结点下标满足：
     • i 的左孩子是 2*i
     • i 的右孩子是 2*i+1
     • i 的父结点是 i/2

     #define MAXSIZE 100  // 顺序存储二叉树的最大容量typedef struct {char data[MAXSIZE];  // 用数组存放结点int length;          // 结点个数（实际元素个数）
     } SqBiTree;
     

   • 不适合一般二叉树，因为可能造成很多空间浪费。
2. 链式存储（链表）
   最常用，每个结点用一个结构体存储：

   typedef struct BiTNode {char data;                  // 数据域struct BiTNode *lchild;     // 左孩子指针struct BiTNode *rchild;     // 右孩子指针
   } BiTNode, *BiTree;
   

二叉树操作

#include <stdio.h>
#include <stdlib.h>// 定义二叉树结点
typedef struct BiTNode {char data;struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;// 创建二叉树（先序输入，空结点用 '#' 表示）
void CreateBiTree(BiTree *T) {char ch;scanf(" %c", &ch); // 读取一个字符if (ch == '#') {*T = NULL; // 空树} else {*T = (BiTNode *)malloc(sizeof(BiTNode));(*T)->data = ch;CreateBiTree(&(*T)->lchild); // 递归创建左子树CreateBiTree(&(*T)->rchild); // 递归创建右子树}
}// 先序遍历
void PreOrder(BiTree T) {if (T != NULL) {printf("%c ", T->data);PreOrder(T->lchild);PreOrder(T->rchild);}
}// 中序遍历
void InOrder(BiTree T) {if (T != NULL) {InOrder(T->lchild);printf("%c ", T->data);InOrder(T->rchild);}
}// 后序遍历
void PostOrder(BiTree T) {if (T != NULL) {PostOrder(T->lchild);PostOrder(T->rchild);printf("%c ", T->data);}
}int main() {BiTree T;printf("请输入二叉树的先序序列（空结点用 # 表示）：\n");CreateBiTree(&T);printf("先序遍历: ");PreOrder(T);printf("\n");printf("中序遍历: ");InOrder(T);printf("\n");printf("后序遍历: ");PostOrder(T);printf("\n");return 0;
}

输入示例：

A B # # C D # # E # #

对应二叉树：

        A/ \B   C/ \D   E

输出结果：

先序遍历: A B C D E 
中序遍历: B A D C E 
后序遍历: B D E C A 

二叉树遍历

二叉树遍历指的是按一定顺序访问二叉树的所有节点。主要有以下几种：

先序遍历（Preorder）

访问顺序：根 → 左子树 → 右子树

递归遍历算法：

#include <stdio.h>
#include <stdlib.h>typedef struct BiTNode {char data;struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;void PreOrder(BiTree T) {if (T) {printf("%c ", T->data);   // 访问根PreOrder(T->lchild);      // 遍历左子树PreOrder(T->rchild);      // 遍历右子树}
}int main() {BiTree root = (BiTree)malloc(sizeof(BiTNode));root->data = 'A';root->lchild = (BiTree)malloc(sizeof(BiTNode));root->lchild->data = 'B';root->rchild = (BiTree)malloc(sizeof(BiTNode));root->rchild->data = 'C';root->lchild->lchild = root->lchild->rchild = NULL;root->rchild->lchild = root->rchild->rchild = NULL;PreOrder(root);return 0;
}

1. 函数定义
   void PreOrder(BiTree T)
   • 函数名PreOrder表示 “前序遍历”。
   • 参数BiTree T：BiTree是二叉树节点的指针类型（通常定义为typedef struct BiTNode *BiTree;），T代表当前遍历的节点。
2. 递归终止条件
   if (T) { ... }
   • 这里的T是指向二叉树节点的指针。若T为NULL（空指针），表示当前节点不存在，此时不执行任何操作（递归终止）；若T非空，则执行遍历逻辑。
3. 前序遍历的核心逻辑
   • printf("%c ", T->data);
     先 “访问根节点”：输出当前节点的数据（T->data）。%c说明节点数据是字符类型。
   • PreOrder(T->lchild);
     再 “遍历左子树”：递归调用PreOrder函数，传入当前节点的左子节点（T->lchild），继续对左子树执行前序遍历。
   • PreOrder(T->rchild);
     最后 “遍历右子树”：递归调用PreOrder函数，传入当前节点的右子节点（T->rchild），继续对右子树执行前序遍历。

假设有如下二叉树（节点数据为字符）：

    A/ \B   C/
D

调用PreOrder(A)（从根节点 A 开始遍历）的过程：

1. 访问 A（输出：A ）；
2. 递归遍历左子树 B：
   • 访问 B（输出：B ）；
   • 递归遍历 B 的左子树 D：
     • 访问 D（输出：D ）；
     • D 无左 / 右子树，递归结束；
   • B 无右子树，递归结束；
3. 递归遍历右子树 C：
   • 访问 C（输出：C ）；
   • C 无左 / 右子树，递归结束；

最终输出结果：A B D C ，符合 “根左右” 的前序遍历规则。

中序遍历（Inorder）

访问顺序：左子树 → 根 → 右子树

递归遍历算法：

void InOrder(BiTree T) {if (T) {InOrder(T->lchild);printf("%c ", T->data);InOrder(T->rchild);}
}

1. 函数定义
   void InOrder(BiTree T)
   • 函数名InOrder表示 “中序遍历”。
   • 参数BiTree T：与前序遍历相同，BiTree是二叉树节点的指针类型（通常定义为typedef struct BiTNode *BiTree;），T代表当前遍历的节点。
2. 递归终止条件
   if (T) { ... }
   • 若T为NULL（空指针），表示当前节点不存在，递归终止（不执行任何操作）；若T非空，则执行中序遍历逻辑。
3. 中序遍历的核心逻辑
   • InOrder(T->lchild);
     先 “遍历左子树”：递归调用InOrder函数，传入当前节点的左子节点（T->lchild），优先深入左子树直至最左侧节点。
   • printf("%c ", T->data);
     再 “访问根节点”：当左子树遍历完成后，输出当前节点的数据（T->data），此处%c说明节点数据为字符类型。
   • InOrder(T->rchild);
     最后 “遍历右子树”：递归调用InOrder函数，传入当前节点的右子节点（T->rchild），对右子树执行中序遍历。

以与前序遍历相同的二叉树为例（节点数据为字符）：

    A/ \B   C/
D

调用InOrder(A)（从根节点 A 开始遍历）的过程：

1. 先递归遍历 A 的左子树 B：
   • 递归遍历 B 的左子树 D：
     • D 无左子树（左子树为NULL），则访问 D（输出：D ）；
     • 再递归遍历 D 的右子树（NULL），无操作；
   • B 的左子树遍历完成，访问 B（输出：B ）；
   • 递归遍历 B 的右子树（NULL），无操作；
2. A 的左子树遍历完成，访问 A（输出：A ）；
3. 递归遍历 A 的右子树 C：
   • C 无左子树（NULL），则访问 C（输出：C ）；
   • 递归遍历 C 的右子树（NULL），无操作；

最终输出结果：D B A C ，严格遵循 “左根右” 的中序遍历规则。

后序遍历（Postorder）

访问顺序：左子树 → 右子树 → 根

递归遍历算法：

void PostOrder(BiTree T) {if (T) {PostOrder(T->lchild);PostOrder(T->rchild);printf("%c ", T->data);}
}

1. 函数定义
   void PostOrder(BiTree T)
   • 函数名PostOrder表示 “后序遍历”。
   • 参数BiTree T：与前序、中序遍历一致，BiTree是二叉树节点的指针类型（通常定义为typedef struct BiTNode *BiTree;），T代表当前遍历的节点。
2. 递归终止条件
   if (T) { ... }
   • 若T为NULL（空指针），表示当前节点不存在，递归终止（不执行任何操作）；若T非空，则执行后序遍历逻辑。
3. 后序遍历的核心逻辑
   • PostOrder(T->lchild);
     先 “遍历左子树”：递归调用PostOrder函数，传入当前节点的左子节点（T->lchild），优先深入左子树直至最左侧节点。
   • PostOrder(T->rchild);
     再 “遍历右子树”：左子树遍历完成后，递归调用PostOrder函数，传入当前节点的右子节点（T->rchild），继续遍历右子树。
   • printf("%c ", T->data);
     最后 “访问根节点”：当左、右子树均遍历完成后，才输出当前节点的数据（T->data），%c说明节点数据为字符类型。

以之前相同的二叉树为例（节点数据为字符）：

    A/ \B   C/
D

调用PostOrder(A)（从根节点 A 开始遍历）的过程：

1. 先递归遍历 A 的左子树 B：
   • 递归遍历 B 的左子树 D：
     • D 无左子树（NULL），无操作；
     • 递归遍历 D 的右子树（NULL），无操作；
     • D 的左、右子树均遍历完成，访问 D（输出：D ）；
   • 递归遍历 B 的右子树（NULL），无操作；
   • B 的左、右子树均遍历完成，访问 B（输出：B ）；
2. 递归遍历 A 的右子树 C：
   • C 无左子树（NULL），无操作；
   • 递归遍历 C 的右子树（NULL），无操作；
   • C 的左、右子树均遍历完成，访问 C（输出：C ）；
3. A 的左、右子树均遍历完成，访问 A（输出：A ）；

最终输出结果：D B C A ，严格遵循 “左右根” 的后序遍历规则。

非递归遍历

非递归先序遍历（Preorder, 根-左-右）

先序遍历的特点是先访问根节点，然后左右子树。非递归通常用 栈 来实现。

#include <stdio.h>
#include <stdlib.h>typedef struct BiTNode {char data;struct BiTNode *lchild, *rchild;
} BiTNode;typedef struct StackNode {BiTNode* data;struct StackNode* next;
} StackNode;void push(StackNode** top, BiTNode* t) {StackNode* node = (StackNode*)malloc(sizeof(StackNode));node->data = t;node->next = *top;*top = node;
}BiTNode* pop(StackNode** top) {if (*top == NULL) return NULL;StackNode* temp = *top;BiTNode* t = temp->data;*top = temp->next;free(temp);return t;
}int isEmpty(StackNode* top) { return top == NULL; }void PreOrderNonRec(BiTNode* root) {StackNode* stack = NULL;BiTNode* p = root;while (p || !isEmpty(stack)) {if (p) {printf("%c ", p->data);  // 访问根push(&stack, p);p = p->lchild;           // 左子树优先} else {p = pop(&stack);p = p->rchild;           // 遍历右子树}}
}

非递归中序遍历（Inorder, 左-根-右）

中序遍历特点是先左子树，再根，再右子树，非递归用栈也是标准做法。

void InOrderNonRec(BiTNode* root) {StackNode* stack = NULL;BiTNode* p = root;while (p || !isEmpty(stack)) {if (p) {push(&stack, p);p = p->lchild;   // 先找左子树} else {p = pop(&stack);printf("%c ", p->data); // 访问根p = p->rchild;   // 遍历右子树}}
}

非递归后序遍历（Postorder, 左-右-根）

后序遍历非递归比较麻烦，可以用 双栈法 或 单栈法 + 上一个访问节点标记。

方法1：双栈法（简单理解）

void PostOrderNonRec(BiTNode* root) {if (!root) return;StackNode *stack1 = NULL, *stack2 = NULL;push(&stack1, root);while (!isEmpty(stack1)) {BiTNode* node = pop(&stack1);push(&stack2, node);if (node->lchild) push(&stack1, node->lchild);if (node->rchild) push(&stack1, node->rchild);}while (!isEmpty(stack2)) {printf("%c ", pop(&stack2)->data);}
}

方法2：单栈法（节省空间）

用一个指针 prev 记录上一次访问的节点，判断是否右子树已访问。

void PostOrderNonRecSingleStack(BiTNode* root) {StackNode* stack = NULL;BiTNode* p = root;BiTNode* prev = NULL;while (p || !isEmpty(stack)) {while (p) {push(&stack, p);p = p->lchild;}p = stack->data; // peekif (p->rchild == NULL || p->rchild == prev) {printf("%c ", p->data);pop(&stack);prev = p;p = NULL;} else {p = p->rchild;}}
}