1 线性模型
所学习的B站视频链接 1 线性模型
文章目录
- 1 模型原理
- 1.1数据集的预处理
- 1.2 模型的引入
- 1.3 使用的方法
- 2 代码编写
1 模型原理
这里我们讲解的是一个线性模型的使用方法
Linear Model
在使用模型的过程中主要有四个步骤
datasetmodelTraininginferring
1.1数据集的预处理
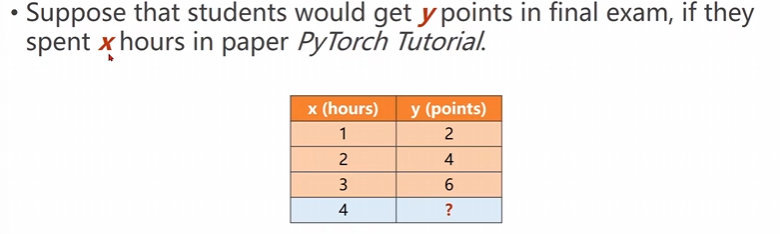
就像上面说到的,在期末考试中已经得到了很多个数据,这些数据是学习时间和最后取得分的关系,求解并推理当x=4x=4x=4的时候这个分数大概是多少y=?y=?y=?。
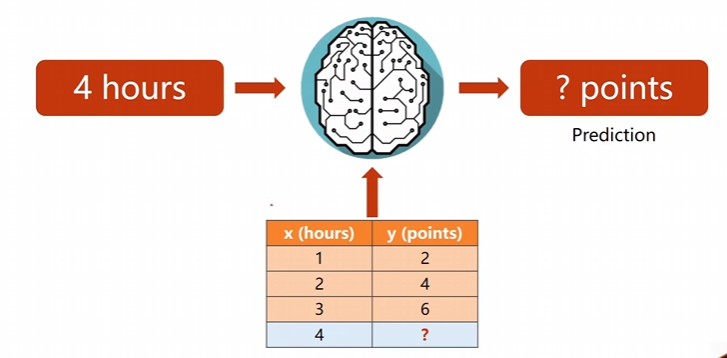
将数据集交付给我们的数据模型,然后我们训练完毕后求推理的目标。
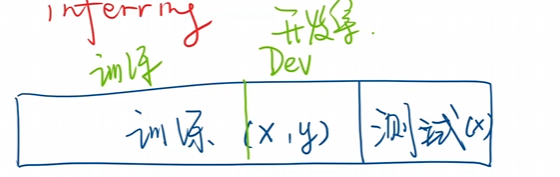
同时在学习过程中我们将已经有答案的数据称为训练集合,在训练集合中还需要分开使用测试集合。
将还未得到输出的数据称为训练模型。
因此我们将自己的数据集合在拿到的时候需要将整个数据分成两份,一份是训练使用,另一份是我们的测试模型。
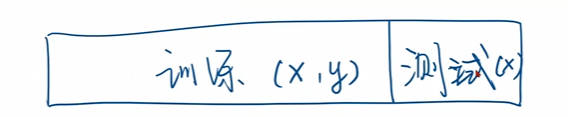
在处理采样数据集合的过程中我们基本上是无法求出数据的真是的分布的哈。
如果在训练的过程中在训练集合的时候,误差特别的小,甚至于将误差都已经学习进来了,这个时候这个训练可以说是过拟合了。因此我们很有可能再一次将训练集进行分开,一部分是训练集,另一部分是开发集,用来泛化模型,让我们的模型更加适合各个误差和输出
1.2 模型的引入
在这里所谓的模型就是想要找到一个比较好的函数y=f(x)y = f(x)y=f(x),能够比较完美的适合这个输入于输出。

现在我们就使用一个线性模型来进行举例。
y上面有一个小帽子表示的是我们自己的预测模型

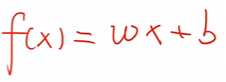
我们要求的就是两个参数w,bw , bw,b
现在我们给出咱们的输入参数和输出的训练集模型。
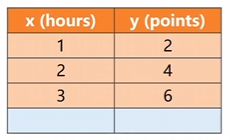
利用上面这个玩意儿来确定w,bw,bw,b并尝试对各个散点进行拟合。
1.3 使用的方法
首先先随便找一组数据看看,这个假设的数据可以引出一组y^\hat{y}y^,这个时候将y^\hat{y}y^和真实数值yyy之间的误差也就是下文的losslossloss(单个样本)。
loss=(y^−y)2=(x∗ω−y)2loss=(\hat{y}-y)^{2}=(x*\omega-y)^{2}loss=(y^−y)2=(x∗ω−y)2
这个就是咱们的损失函数,要让这个拟合的越好,那么必定有损失函数的数据越小。
如果有多个样本的话咱们需要计算所有样本的平均损失。
$cost=1N∑n=1N(y^n−yn)2cost=\frac{1}{N}\sum_{n=1}^N(\hat{y}_n-y_n)^2cost=N1n=1∑N(y^n−yn)2$
因此我们真正需要的就是求出一组数据w,bw,bw,b,使得该模型的平均损失达到最小即可。

MSE平均平方误差。
这个时候可以根据这样的公式进行损失上面的一个计算。
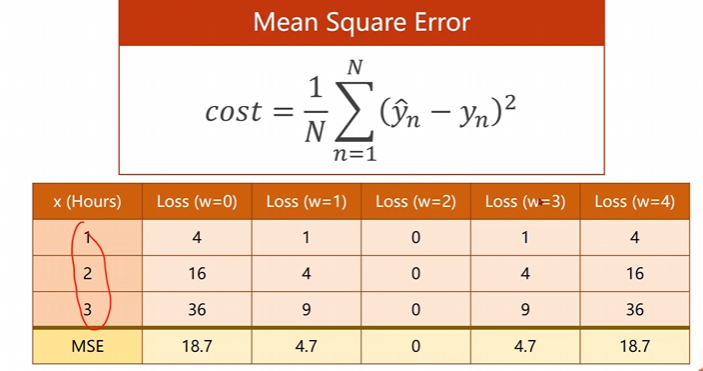
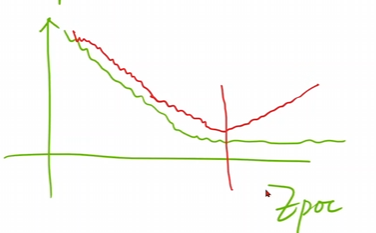
那我们怎么样求出这样的好数据呢,如果数据比较少,那么方法非常简单,我们可以使用暴力枚举法进行求解,也就是穷举法,求出在某一段部分中损失和w之间的关系曲线,并给出曲线最低点的数据即可。
2 代码编写
这里采用的穷举法进行实现的
具体的文件路径[穷举法的线性模型](E:\code\4.DeepLearning_basis\2 WithLiu2Da\1 线性模型.py)
在深度学习过程之中对可视化的操作和处理是十分的重要的,一定要学会进行绘图的绘制。
让模型在训练的过程之中时实绘制可视化图形,毕竟这玩意儿一开始就是一两天,一周之类的。
这个模型是最简单的y=wxy = wxy=wx
import numpy as np
import matplotlib.pyplot as pltx_data = [1.0 , 2.0 , 3.0 , 4.0 , 5.0]
y_data = [2.0 , 4.0 , 6.0 , 8.0 , 10.0]def forward(x):return x * wdef MSE_loss(x , y):y_hat = forward(x)res = (y_hat - y)**(2)return resw_list = []
mse_loss = []for w in np.arange(0.0 , 4.1 , 0.1):w_list.append(w)sum = 0for x , y in zip(x_data , y_data):sum += MSE_loss(x , y)sum = sum/(len(x_data))mse_loss.append(sum)plt.plot(w_list , mse_loss)
plt.scatter(w_list , mse_loss , color = 'r' ,s = 20 )
plt.xlabel('W')
plt.ylabel('MSE')
plt.show()print(w_list)
print(mse_loss)
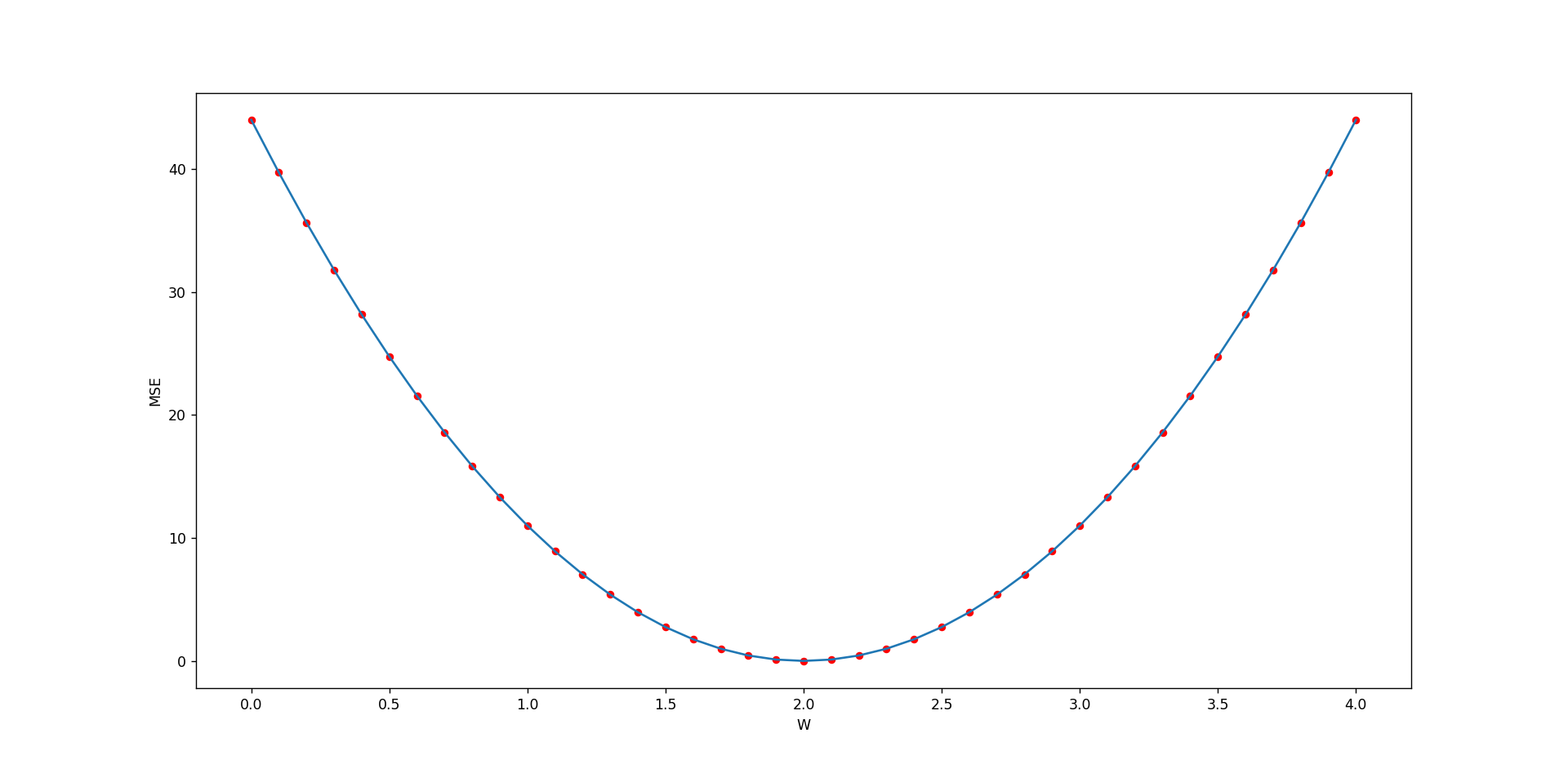
稍微难一点点的y=wx+by = wx+by=wx+b
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3Dx_data = [1.0, 2.0, 3.0, 4.0, 5.0]
y_data = [4.0, 6.0, 8.0, 10.0, 12.0]def forward(x, w, b):return x * w + bdef loss(x, y, w, b):return ((forward(x, w, b) - y) * (forward(x, w, b) - y))# 生成w和b的网格
w_range = np.arange(0, 4.1, 0.1)
b_range = np.arange(0, 4.1, 0.1)
W, B = np.meshgrid(w_range, b_range)# 计算每个(w,b)组合的MSE
MSE = np.zeros_like(W)for i in range(len(w_range)):for j in range(len(b_range)):w_val = w_range[i]b_val = b_range[j]total_loss = 0for x, y in zip(x_data, y_data):total_loss += loss(x, y, w_val, b_val)MSE[j, i] = total_loss / len(x_data) # 注意索引顺序min_idx = np.unravel_index(np.argmin(MSE, axis=None), MSE.shape)
min_w = w_range[min_idx[1]]
min_b = b_range[min_idx[0]]
min_mse = MSE[min_idx]fig = plt.figure(figsize=(12,9))
ax = fig.add_subplot(111 , projection='3d')ax.scatter(min_w, min_b, min_mse, color='red', s=100, label=f'Min MSE: {min_mse:.2f}\nw={min_w:.1f}, b={min_b:.1f}')surf = ax.plot_surface(W , B , MSE , cmap='viridis',alpha = 0.8 , linewidth = 0 , antialiased = True)
ax.set_xlabel('Weight (w)', fontsize=12)
ax.set_ylabel('Bias (b)', fontsize=12)
ax.set_zlabel('MSE Loss', fontsize=12)
ax.set_title('MSE Loss Surface for Linear Regression y = w*x + b', fontsize=14)
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=20, label='MSE Value')
ax.legend()ax.view_init(elev=25, azim=40)
plt.tight_layout()
plt.show()print(f"Minimum MSE: {min_mse:.4f} at w={min_w:.1f}, b={min_b:.1f}")
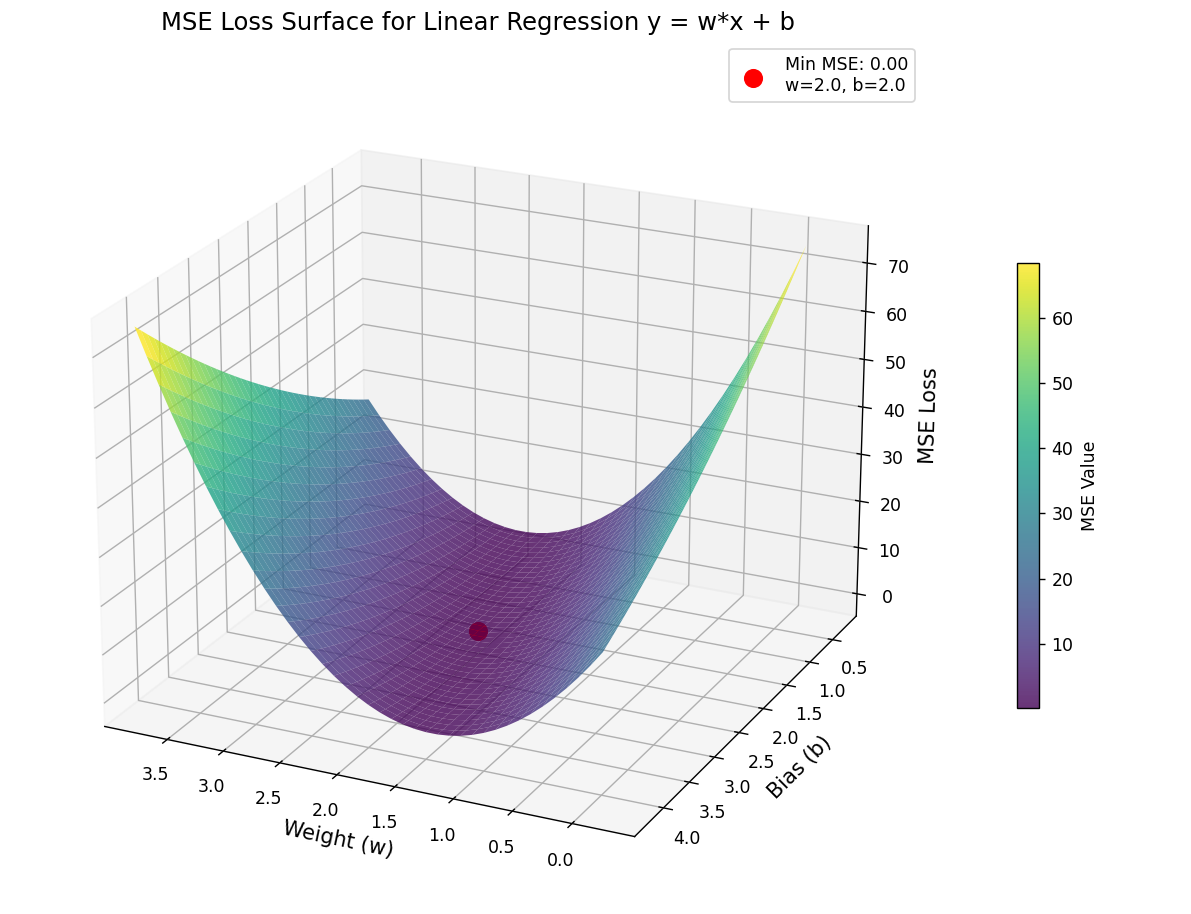
这个是用穷举法的使用,来模拟所谓的线性模型。
以后也是画图,但是要绘制的是误差和轮数之间的关系。这一点就非常的重要了。