数据挖掘5.3 PCA主成分分析降维

Principal Component Analysis (PCA) 主成分分析

降维 Dimensionality Reduction

矩阵 $X$ 的维度为：

$$X\in {\mathbb{R}}^{N\times d}$$

$N$ ：样本数量 (number of samples)
$d$ ：特征维度 (number of features)

降维后，$d$会变小。

比如，[10,1]降维后变成[10]，直接删除一个维度，是最简单直接的降维方式（当然会有很多问题）。

PCA

PCA 是投影，本质是降维。PCA是实现这一点的方法，一种数据变换的方法 (A method for transforming the data)

将数据投影到一组正交向量上，使得投影后数据的方差最大。

在方向 $w$ 上的投影公式：
$$z=w^{T}x$$

目标是找到使投影方差最大的方向$w$：
$$\underset{w}{\max }Var(z)$$

PCA降维，投影到一个单位向量方向，各个数据点方差最大，这是第一主成分。与第一主成分的正交（垂直）的方向单位向量，是第二主成分。

投影值怎么计算

举个栗子
$$a_1=\left[\begin{array}{c}2\\ 3\end{array}\right]$$
我们想要把它投影到 $x$ 轴，于是点乘 $w=\left[\begin{array}{c}1\\ 0\end{array}\right]$，
$$w^T{a}_1=\left[\begin{array}{cc}1& 0\end{array}\right]\left[\begin{array}{c}2\\ 3\end{array}\right]=[2]$$
如果我们想要把它投影到 $y$ 轴，于是点乘 $w=\left[\begin{array}{c}0\\ 1\end{array}\right]$，
$$w^T{a}_1=\left[\begin{array}{cc}0& 1\end{array}\right]\left[\begin{array}{c}2\\ 3\end{array}\right]=[3]$$

由此可见，如果想要把一个点投影到别的轴上，点乘这个轴的单位方向向量就可以了。

如何实现：朴素方法 (Naïve Implementation)

设置 $p=0$
对 $p$ 从 $0$ 到 $\pi$ 进行迭代（分步）：

• 计算投影向量 (projection vector)：
  $$w_p=\left[\begin{array}{c}\cos (p)\\ \sin (p)\end{array}\right]$$

• 将数据投影到该方向：
  $$z_i=w_p^T{x}_i$$

• 计算投影后数据的方差 (variance)。

• 绘制方差随 $p$ 变化的曲线。
  

• 找到使方差最大的 $p$。

主成分分析 (PCA) 的直观实现：
通过不同角度 $p$ 的方向向量 $w_p$ 投影数据；
计算投影后的方差；
找到方差最大的方向，这个方向就是 **第一主成分**。

具体计算推导

1 PCA投影方差计算——max $w^{T}Cw$，C协方差矩阵

投影方差最大——> max $w^{T}Cw$，C是协方差矩阵，以下是推导过程，

主成分分析 (PCA)：投影方差与协方差矩阵的关系
定义数据在方向 $w$ 上的投影：
$$z=w^{T}x$$

投影的方差：
$$Var(z)=Var(w^{T}x)=E[(w^{T}x-w^T\mu {)}^2]$$

展开：
$$\begin{gathered} =E[(w^T(x-\mu ))(w^T(x-\mu ))] \\ =E[w^T(x-\mu )(x-\mu {)}^{T}w] \end{gathered}$$
提取常数 $w$：
$$=w^{T}E[(x-\mu )(x-\mu {)}^T]w$$

协方差矩阵公式：
$$Cov(x)=E[(x-\mu )(x-\mu {)}^T]=C$$

最终推出：
$$Var(z)=w^{T}Cw$$

数据在方向 $w$上的投影方差 $=w^{T}Cw$，而 PCA 就是寻找让这个这个投影方差最大的方向 $w$。

2 max $w^{T}Cw$——求解主成分方向 $w$

目标，希望找到一个单位向量 $w$，使得投影后的方差最大：
$$\underset{w}{\max }Var(z_1)=w^{T}Cw$$
约束条件是 $w^{T}w=1$

其中 $C$ 是协方差矩阵。

拉格朗日乘子法 (Lagrange Multipliers)

将带约束的优化问题转化为拉格朗日函数（把带约束的优化问题转成无约束问题）：

$$L(w,\alpha )=w^{T}Cw-\alpha (w^{T}w-1)$$
所求为 $max{w}^{T}Cw$，也就是 $maxL(w,\alpha )$。

对 $w$ 求导

$$\frac{\partial L}{\partial w}=2Cw-2\alpha w=0$$

$$Cw=\alpha w$$

• $w$ 是协方差矩阵 $C$ 的 特征向量
• $\alpha$ 是对应的 特征值
• 使方差最大的方向，就是 **最大特征值对应的特征向量**

最终，我们所要求最大化投影方差，只要求协方差矩阵的特征向量就行了。

PCA 在降维中的应用

协方差矩阵中较小的特征值对应的方向对总方差贡献很小，可以舍弃而不会丢失太多信息。
我们通常保留累计贡献率达到 90% 的前 $k$ 个特征值和特征向量。

方差贡献率 (Proportion of Variance, PoV)

Proportion of Variance Explained (累计方差贡献率曲线)

横轴 (Eigenvectors)：主成分个数 $k$
纵轴 (Prop of Var)：累计方差贡献率（PoV）
曲线随 $k$ 增大而上升，并逐渐接近 1。

在图中，当 k≈20 时，累计方差贡献率已经接近 90%，说明只需保留前 20 个主成分，就能保留大部分信息。

$$PoV(k)=\frac{{\lambda }_1+{\lambda }_2+\cdots +{\lambda }_k}{{\lambda }_1+{\lambda }_2+\cdots +{\lambda }_d}$$

其中：

• ${\lambda }_i$ 为特征值，且按从大到小排序
• $d$ 为原始数据的维度
• $k<d$ 为选择保留的主成分数

如何选择 $k$

一般当 $PoV>0.9$ 时可以停止。
也可以通过 碎石图 (Scree Plot) 找“肘点 (elbow)”来确定 $k$。

Scree Graph (碎石图)
横轴 (Eigenvectors)：特征向量的索引（对应主成分的序号）。
纵轴 (Eigenvalues)：对应的特征值大小（代表方差贡献）。

数据投影：将 $d$ 维数据 $x$ （均值向量为 $\mu$）投影到 $k$ 维子空间，使用 $k\times d$ 的投影矩阵 $W$

$$z=W^T(x-\mu )$$

其中：

• $W$ 包含前 $k$ 个特征向量
• $z$ 是新的 $k$ 维数据表示

PCA：重建与重建误差 (Reconstruction & Error)

1. PCA 投影

在 PCA 中，数据 $x$ 被投影到低维空间：

$$z=W^T(x-\mu )$$

其中：

• $x$ ：原始 $d$ 维数据向量
• $\mu$ ：均值向量
• $W$ ：$d\times k$ 的投影矩阵（由前 $k$ 个特征向量组成）
• $z$ ：新的 $k$ 维数据表示

2. PCA 重建

从低维表示 $z$ 还原回高维近似数据：

$$\hat{x}=Wz+\mu$$

因为 $W$ 的列向量是正交的，有 $W{W}^T=I$。

3. 重建误差

定义为原始数据 $x$ 与重建数据 $\hat{x}$ 的差异：

$$E_{rec}=\sum _{t=1}^N\Vert {\hat{x}}^t-x^t\Vert$$

其中：

• $N$ ：样本总数
• ${\hat{x}}^t$ ：第 $t$ 个样本的重建结果
• $x^t$ ：第 $t$ 个原始样本

4. 含义

• 重建误差越小，说明保留的主成分越能代表原始数据。
• 当 $k=d$ 时（即不降维），重建误差为 0。
• 当 $k<d$ 时，误差取决于被舍弃的特征值大小。

PCA的缺陷

在图像中的应用

在不影响预测准确率的情况下，第一个主成分可能并不总是最佳主成分。

PCA的愚蠢

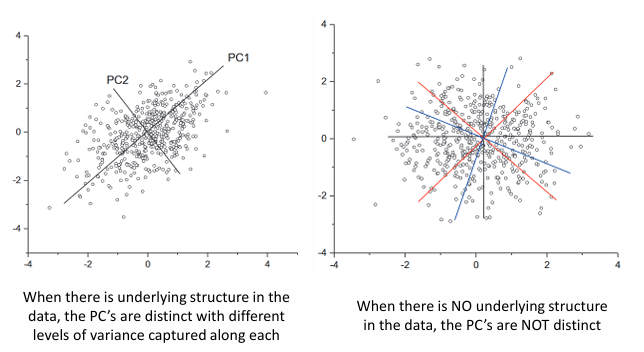
PCA是一种愚蠢的算法，它在代码中实现，你给它数据，它就会输出主成分。尽管有些数据被我们解释为最大方差的方向，但事实可能并不是，比如右图。这取决于数据集的选择。如果数据集类似左边，它可以给出一些最大方差的方向。但如果像右边这样，那就完全没有意义。