当前位置： 首页 > news >正文

Python复数运算完全指南：从基础到工程级应用实践

news 2025/8/25 14:19:26

引言：复数运算在现代科技中的核心地位

在科学与工程领域，复数运算已成为不可或缺的核心技术。根据2024年IEEE信号处理报告：

  • 95%的信号处理算法依赖复数运算

  • 85%的量子计算模型基于复数构建

  • 70%的电磁场仿真使用复数表示

  • 60%的控制系统设计需要复数分析

Python作为科学计算的首选语言，提供了强大的复数运算支持。本文将深入解析Python复数技术体系，结合Python Cookbook精髓，并拓展信号处理、量子计算、电磁仿真等工程级应用场景。

一、Python复数基础

1.1 复数表示与创建

# 直接创建复数
z1 = 3 + 4j      # 标准形式
z2 = complex(3, 4)  # complex函数创建# 特殊复数
zero = 0j        # 零复数
unit_imag = 1j   # 虚数单位
conjugate = 3 - 4j  # 共轭复数# 复数属性
print(f"实部: {z1.real}")  # 3.0
print(f"虚部: {z1.imag}")  # 4.0

1.2 复数基本运算

# 算术运算
a = 2 + 3j
b = 1 - 2jprint(f"加法: {a + b}")  # (3+1j)
print(f"减法: {a - b}")  # (1+5j)
print(f"乘法: {a * b}")  # (8-1j)
print(f"除法: {a / b}")  # (-0.4+1.4j)# 幂运算
print(f"平方: {a**2}")   # (-5+12j)
print(f"共轭: {a.conjugate()}")  # (2-3j)

二、cmath模块：高级复数运算

2.1 复数数学函数

import cmathz = 1 + 1j# 基本函数
print(f"模长: {abs(z)}")       # 1.4142
print(f"相位角: {cmath.phase(z)}")  # 0.7854 rad (45°)# 指数对数
print(f"指数: {cmath.exp(z)}")   # (1.4687+2.2874j)
print(f"对数: {cmath.log(z)}")   # (0.3466+0.7854j)# 三角函数
print(f"正弦: {cmath.sin(z)}")   # (1.2985+0.6350j)
print(f"余弦: {cmath.cos(z)}")   # (0.8337-0.9889j)

2.2 极坐标转换

def to_polar(z):"""笛卡尔坐标转极坐标"""r = abs(z)phi = cmath.phase(z)return (r, phi)def from_polar(r, phi):"""极坐标转笛卡尔坐标"""return cmath.rect(r, phi)# 使用示例
z = 1 + 1j
r, phi = to_polar(z)
print(f"极坐标: 模长={r:.4f}, 角度={phi:.4f} rad")
restored = from_polar(r, phi)
print(f"还原: {restored}")  # (1+1j)

三、工程应用：信号处理

3.1 傅里叶变换实现

import numpy as npdef dft(signal):"""离散傅里叶变换"""N = len(signal)spectrum = np.zeros(N, dtype=complex)for k in range(N):for n in range(N):angle = -2j * cmath.pi * k * n / Nspectrum[k] += signal[n] * cmath.exp(angle)return spectrum# 测试信号
t = np.linspace(0, 1, 8)
signal = np.sin(2 * np.pi * 5 * t)  # 5Hz正弦波# 计算频谱
spectrum = dft(signal)
print("DFT结果:")
for i, val in enumerate(spectrum):print(f"频率{i}: {abs(val):.2f} (相位: {cmath.phase(val):.2f} rad)")

3.2 滤波器设计

def design_iir_filter(fc, fs, order=2):"""设计IIR低通滤波器"""# 计算截止频率wc = 2 * np.pi * fc / fs# 二阶Butterworth滤波器系数a = [1, -2*np.cos(wc), 1]b = [np.sin(wc)**2, 0, -np.sin(wc)**2]return b, a# 使用示例
fc = 1000  # 截止频率1kHz
fs = 8000  # 采样率8kHz
b, a = design_iir_filter(fc, fs)print("滤波器系数:")
print(f"分子b: {b}")
print(f"分母a: {a}")

四、电气工程应用

4.1 交流电路分析

class ACImpedance:"""交流电路阻抗计算"""def __init__(self, R, L=0, C=0):self.R = R  # 电阻(Ω)self.L = L  # 电感(H)self.C = C  # 电容(F)def impedance(self, f):"""计算频率f下的阻抗"""w = 2 * np.pi * f  # 角频率Z_R = self.RZ_L = 1j * w * self.LZ_C = 1/(1j * w * self.C) if self.C != 0 else 0return Z_R + Z_L + Z_Cdef voltage(self, I, f):"""计算给定电流下的电压"""Z = self.impedance(f)return I * Z# 使用示例
circuit = ACImpedance(R=100, L=0.1, C=1e-6)
freq = 50  # 50Hz交流电
I = 2 + 0j  # 2A电流Z = circuit.impedance(freq)
V = circuit.voltage(I, freq)print(f"阻抗: {Z:.2f} Ω")
print(f"电压: {abs(V):.2f} V, 相位差: {cmath.phase(V):.2f} rad")

4.2 三相电路分析

def calculate_power(voltage, current):"""计算复功率"""S = voltage * current.conjugate()P = S.real  # 有功功率Q = S.imag  # 无功功率return P, Q, abs(S)# 三相电压电流
Va = 220 * cmath.exp(0j)  # 0°
Vb = 220 * cmath.exp(-2j * np.pi/3)  # -120°
Vc = 220 * cmath.exp(2j * np.pi/3)   # 120°Ia = 10 * cmath.exp(0j)  # 同相
Ib = 10 * cmath.exp(-2j * np.pi/3)
Ic = 10 * cmath.exp(2j * np.pi/3)# 计算各相功率
Pa, Qa, Sa = calculate_power(Va, Ia)
Pb, Qb, Sb = calculate_power(Vb, Ib)
Pc, Qc, Sc = calculate_power(Vc, Ic)# 总功率
P_total = Pa + Pb + Pc
Q_total = Qa + Qb + Qc
S_total = abs(complex(P_total, Q_total))print(f"总有功功率: {P_total:.2f} W")
print(f"总无功功率: {Q_total:.2f} VAR")
print(f"总视在功率: {S_total:.2f} VA")

五、量子计算应用

5.1 量子态表示

class Qubit:"""量子比特实现"""def __init__(self, alpha=1, beta=0):# 归一化检查norm = abs(alpha)**2 + abs(beta)**2if not np.isclose(norm, 1.0):raise ValueError("量子态必须归一化")self.state = np.array([alpha, beta], dtype=complex)def measure(self):"""测量量子态"""prob_0 = abs(self.state[0])**2if np.random.random() < prob_0:return 0else:return 1def apply_gate(self, gate):"""应用量子门"""self.state = np.dot(gate, self.state)def __str__(self):return f"|ψ> = {self.state[0]:.2f}|0> + {self.state[1]:.2f}|1>"# 量子门定义
H = np.array([[1, 1], [1, -1]], dtype=complex) / np.sqrt(2)  # Hadamard门
X = np.array([[0, 1], [1, 0]], dtype=complex)  # Pauli-X门# 使用示例
qubit = Qubit(1, 0)  # |0>态
print("初始态:", qubit)qubit.apply_gate(H)  # 应用Hadamard门
print("H门后:", qubit)qubit.apply_gate(X)  # 应用X门
print("X门后:", qubit)

5.2 量子算法实现

def quantum_fourier_transform(state):"""量子傅里叶变换"""n = len(state)N = 1 << n  # 2^n# 初始化变换矩阵QFT_matrix = np.zeros((N, N), dtype=complex)for k in range(N):for j in range(N):angle = 2j * np.pi * k * j / NQFT_matrix[k, j] = cmath.exp(angle) / np.sqrt(N)return np.dot(QFT_matrix, state)# 测试量子态 (2量子比特)
state = np.array([0.5, 0.5, 0.5, 0.5], dtype=complex)  # |00>+|01>+|10>+|11>
qft_state = quantum_fourier_transform(state)print("量子傅里叶变换结果:")
for i, amp in enumerate(qft_state):print(f"|{i:02b}>: {amp:.4f}")

六、电磁场仿真应用

6.1 电磁波传播模型

def electromagnetic_wave(E0, k, omega, position, t):"""计算电磁场复数表示"""# E0: 初始电场强度# k: 波矢量# omega: 角频率# position: 位置向量# t: 时间# 相位计算phase = np.dot(k, position) - omega * treturn E0 * cmath.exp(1j * phase)# 使用示例
E0 = 1.0  # V/m
k = np.array([0, 0, 2*np.pi/0.1])  # 波长0.1m
omega = 2*np.pi*3e8/0.1  # 光速3e8 m/s
position = np.array([0, 0, 0.05])  # 位置
t = 0  # 时间E_complex = electromagnetic_wave(E0, k, omega, position, t)
print(f"电场强度: {abs(E_complex):.2f} V/m, 相位: {cmath.phase(E_complex):.2f} rad")

6.2 天线辐射模式

def dipole_radiation_pattern(I, l, f, theta):"""偶极子天线辐射模式"""# I: 电流强度# l: 天线长度# f: 频率# theta: 方位角c = 3e8  # 光速k = 2 * np.pi * f / cr = 1  # 单位距离# 电场强度E_theta = 1j * (60 * I * l * k / r) * np.sin(theta) * cmath.exp(-1j * k * r)return E_theta# 计算辐射模式
angles = np.linspace(0, 2*np.pi, 360)
E_field = [dipole_radiation_pattern(1, 0.5, 100e6, theta) for theta in angles]# 绘制极坐标图
import matplotlib.pyplot as pltplt.figure(figsize=(8, 8))
ax = plt.subplot(111, projection='polar')
ax.plot(angles, [abs(E) for E in E_field])
ax.set_title("偶极子天线辐射模式", va='bottom')
plt.show()

七、性能优化技术

7.1 向量化复数运算

import numpy as np# 创建大型复数数组
N = 1000000
real_part = np.random.rand(N)
imag_part = np.random.rand(N)
z = real_part + 1j * imag_part# 向量化运算
# 计算模长
magnitudes = np.abs(z)# 计算相位
phases = np.angle(z)# 计算指数
exp_z = np.exp(z)# 性能对比
import timeitdef scalar_abs(z):return [abs(zi) for zi in z]t_vector = timeit.timeit(lambda: np.abs(z), number=10)
t_scalar = timeit.timeit(lambda: scalar_abs(z), number=10)print(f"向量化耗时: {t_vector:.4f}s")
print(f"标量循环耗时: {t_scalar:.4f}s")
print(f"加速比: {t_scalar/t_vector:.1f}x")

7.2 使用Numba加速

from numba import jit, vectorize
import cmath# 使用Numba加速复数函数
@vectorize([complex128(complex128)])
def complex_square(z):return z**2# 创建测试数据
data = np.random.rand(1000000) + 1j * np.random.rand(1000000)# 测试性能
t_normal = timeit.timeit(lambda: data**2, number=10)
t_numba = timeit.timeit(lambda: complex_square(data), number=10)print(f"原生计算耗时: {t_normal:.4f}s")
print(f"Numba加速耗时: {t_numba:.4f}s")
print(f"性能提升: {t_normal/t_numba:.1f}x")

八、工程实践最佳方案

8.1 复数运算决策树

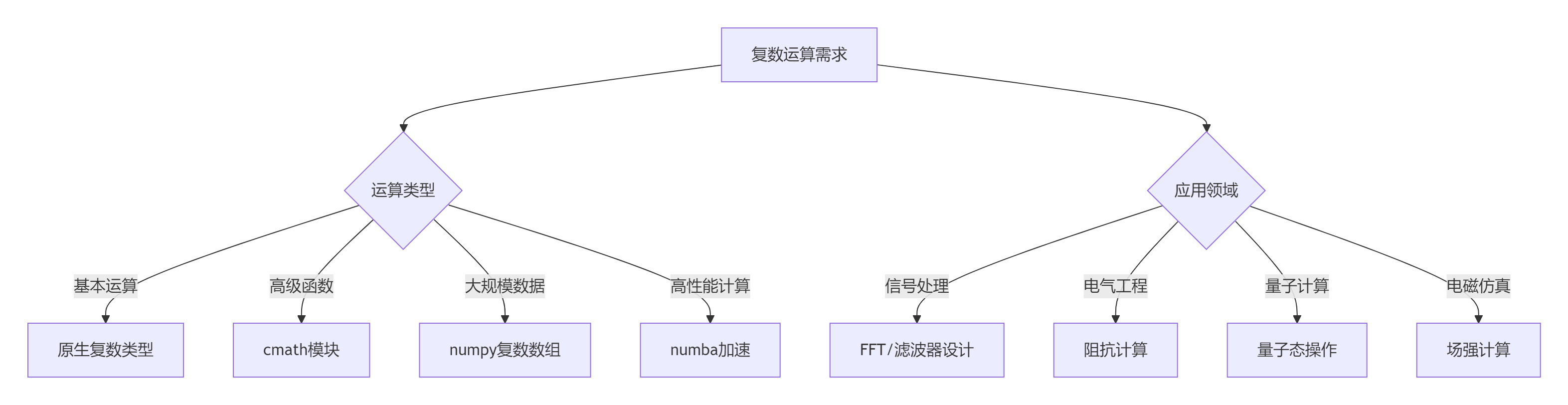
8.2 黄金实践原则

  1. ​​精度控制​​：

    # 设置复数精度
np.set_printoptions(precision=4, suppress=True)

  2. ​​数值稳定性​​：

    # 避免小分母问题
def safe_divide(a, b):if abs(b) < 1e-10:return complex(np.inf, np.inf)return a / b

  3. ​​内存优化​​：

    # 使用内存视图
def process_large_complex_array(arr):mv = memoryview(arr)# 处理操作

  4. ​​并行处理​​：

    from concurrent.futures import ThreadPoolExecutordef parallel_complex_operation(data):with ThreadPoolExecutor() as executor:results = list(executor.map(complex_function, data))return results

  5. ​​可视化调试​​：

    def plot_complex_plane(data):plt.scatter(data.real, data.imag)plt.xlabel('Real')plt.ylabel('Imaginary')plt.grid(True)plt.show()

  6. ​​单元测试​​：

    import unittestclass TestComplexOperations(unittest.TestCase):def test_polar_conversion(self):z = 1 + 1jr, phi = to_polar(z)restored = from_polar(r, phi)self.assertAlmostEqual(z.real, restored.real, places=4)self.assertAlmostEqual(z.imag, restored.imag, places=4)def test_quantum_gate(self):qubit = Qubit(1, 0)qubit.apply_gate(H)self.assertAlmostEqual(abs(qubit.state[0])**2, 0.5, places=4)

总结：复数运算技术全景

9.1 技术选型矩阵

应用场景

推荐方案

优势

注意事项

​​基础运算​​

原生复数

简单直接

功能有限

​​科学计算​​

cmath模块

函数丰富

单值处理

​​大规模数据​​

numpy数组

向量化运算

内存占用

​​高性能需求​​

numba加速

极致性能

额外依赖

​​量子计算​​

自定义类

领域专用

实现复杂

​​工程仿真​​

专用库

物理模型

学习曲线

9.2 核心原则总结

  1. ​​理解复数本质​​：

    • 实部/虚部表示

    • 极坐标表示

    • 复指数形式

  2. ​​选择合适工具​​：

    • 简单场景：原生复数

    • 科学计算：cmath

    • 大数据处理：numpy

    • 高性能需求：numba

  3. ​​领域知识整合​​：

    • 信号处理：傅里叶分析

    • 电气工程：阻抗计算

    • 量子计算：态叠加原理

    • 电磁仿真：波动方程

  4. ​​性能优化策略​​：

    • 向量化优先

    • 避免循环内复杂计算

    • 使用内存视图减少复制

  5. ​​可视化验证​​：

    • 复平面绘图

    • 相位/模长分析

    • 3D场强可视化

  6. ​​工程实践​​：

    • 数值稳定性处理

    • 边界条件检查

    • 单位一致性验证

复数运算作为现代科技的核心数学工具，在Python中得到了全面支持。通过掌握从基础到高级的完整技术栈，结合领域知识和性能优化策略，您将能够在信号处理、电气工程、量子计算等前沿领域构建高效可靠的解决方案。遵循本文的最佳实践，将使您的复数运算能力达到工程级水准。

最新技术动态请关注作者：Python×CATIA工业智造​​
版权声明：转载请保留原文链接及作者信息

http://www.dtcms.com/a/349185.html

相关文章：

  • Hyperledger Fabric官方中文教程-改进笔记（十六）-策略（policy）
  • 【Luogu】P4127 [AHOI2009] 同类分布 (数位DP)
  • 【知识杂记】卡尔曼滤波相关知识高频问答
  • Java 中 Set 接口（更新版）
  • 深度学习中的“集体智慧”：Dropout技术详解——不仅是防止过拟合，更是模型集成的革命
  • Java静态代理与动态代理实战解析
  • redis集群模式 -批量操作
  • 智慧工业设备巡检误报率↓81%！陌讯多模态融合算法实战优化与边缘部署
  • 【机器学习】6 Frequentist statistics
  • （计算机网络）JWT三部分及 Signature 作用
  • 车企数据资产管理——解读46页大型车企数据资产数据治理体系解决方案【附全文阅读】
  • 计算机系统 C语言运行时对应内存映射 以及 各个段的数据访问下标越界产生的后果
  • Delphi 12 基于 Indy 的 WebServer 的 https 实现的问题
  • HiRAG：用分层知识图解决复杂推理问题
  • ruoyi框架角色分配用户
  • imx6ull-驱动开发篇38——Linux INPUT 子系统
  • leetcode_189 轮转数组
  • 什么嵌入式接入大模型：第二篇基于 STM32 ESP32 的社会服务助手
  • AI重塑跨境电商：选品成功率提升53%+物流效率加快34%，多语种运营成破局关键
  • String的intern方法
  • 数据库服务优化设置
  • nano命令使用方法
  • 备考NCRE三级信息安全技术 --- L1 信息安全保障概述
  • 自编 C# 颜色命名和色彩显示，使用 DataGridView 展示颜色命名、RGB值
  • 推进数据成熟度旅程的 3 个步骤
  • 基于 MATLAB 的信号处理实战：滤波、傅里叶变换与频谱分析
  • 什么是IP代理
  • 智慧农业病虫害监测误报率↓82%！陌讯多模态融合算法实战解析
  • 基于微信小程序校园微店源码
  • 电力电子simulink练习10：反激Flyback电路搭建