java-代码随想录第十五天| 12.平衡二叉树、222.完全二叉树的节点个数、404.左叶子之和
目录
12.平衡二叉树
222.完全二叉树的节点个数
404.左叶子之和
思路参考:代码随想录
12.平衡二叉树
链接:110. 平衡二叉树 - 力扣(LeetCode)
题目:给定一个二叉树,判断它是否是 平衡二叉树
题解:
1、如何判断当前传入节点为根节点的二叉树是否是平衡二叉树?左子树高度和右子树高度的差值。分别求出左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则返回-1,表示已经不是二叉平衡树了。
2、如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没意义了。
如果已经不是二叉平衡树了,可以返回-1来标记已经不符合平衡树的规则了。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isBalanced(TreeNode root) {return getHeight(root) != 1;}private int getHeight(TreeNode root){if(root == null){return 0;}int leftHeight=getHeight(root.left);if(leftHeight == -1){return -1;}int rightHeight=getHeight(root.left);if(rightHeight == -1){return -1;}if(Math.abs(leftHeight-rightHeight) > 1){return -1;}return Math.max(leftHeight,rightHeight)+1;}
}222.完全二叉树的节点个数
链接:222. 完全二叉树的节点个数 - 力扣(LeetCode)
题目:
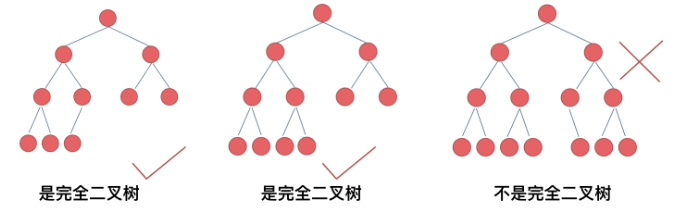
给你一棵 完全二叉树 的根节点
root,求出该树的节点个数。完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第
h层(从第 0 层开始),则该层包含1~ 2h个节点。
题解:
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层节点都集中在该层最左边的若干位置。若最底层为第h层,则该层包含1~2^(h-1)个节点。
左子树的节点数+右子树的节点数+当前根节点。
递归终止条件:空节点计数为0。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int countNodes(TreeNode root) {if(root == null){return 0;}return countNodes(root.left)+countNodes(root.right)+1;}
}404.左叶子之和
链接:404. 左叶子之和 - 力扣(LeetCode)
题目:给定二叉树的根节点
root,返回所有左叶子之和。
题解:
1.左叶子不是二叉树左侧节点
2.左叶子定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点。
3.判断依据:如果该节点的左节点不为空,左节点的左节点不为空,左节点的右节点不为空,则该节点为左叶子
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int sumOfLeftLeaves(TreeNode root) {//如果该节点的左节点不为空,左节点的左节点不为空,左节点的右节点不为空,则该节点为左叶子if(root == null) return 0;//计算左子树所有的左叶子之和int leftValue=sumOfLeftLeaves(root.left);//计算右子树所有的左叶子之和int rightValue=sumOfLeftLeaves(root.right);//计算当前节点左叶子的值int midValue=0;if(root.left != null && root.left.left == null && root.left.right == null){midValue= root.left.val;}int sum=midValue+leftValue+rightValue;return sum; }
}