leetcode 1504. 统计全 1 子矩形 中等
给你一个 m x n 的二进制矩阵 mat ,请你返回有多少个 子矩形 的元素全部都是 1 。
示例 1:
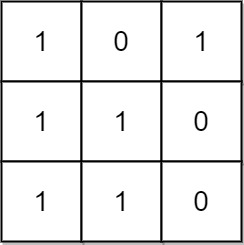
输入:mat = [[1,0,1],[1,1,0],[1,1,0]] 输出:13 解释: 有 6 个 1x1 的矩形。 有 2 个 1x2 的矩形。 有 3 个 2x1 的矩形。 有 1 个 2x2 的矩形。 有 1 个 3x1 的矩形。 矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
示例 2:
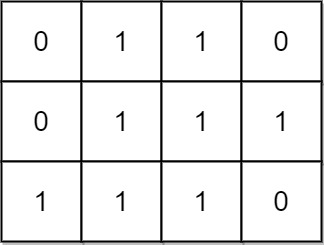
输入:mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] 输出:24 解释: 有 8 个 1x1 的子矩形。 有 5 个 1x2 的子矩形。 有 2 个 1x3 的子矩形。 有 4 个 2x1 的子矩形。 有 2 个 2x2 的子矩形。 有 2 个 3x1 的子矩形。 有 1 个 3x2 的子矩形。 矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。
提示:
1 <= m, n <= 150mat[i][j]仅包含0或1
分析:遍历矩阵,用一个数组记录连续 1 的长度。之后从第 i 行开始自下而上枚举。第 i 行,满足条件的子矩形有 row[i][j] 个;第 i−1 行,满足条件的子矩形有 min(row[i][j],row[i−1][j]) 个,因为得这两行全为 1 才满足条件。再往上也是一样,得一直取最小值才能满足条件。
int numSubmat(int** mat, int matSize, int* matColSize) {int n=matSize,m=matColSize[0],ans=0;;int pre[n+5][m+5];for(int i=0;i<n;++i){for(int j=0;j<m;++j){pre[i][j]=0;if(mat[i][j]==1)pre[i][j]=pre[i][j-1>=0?j-1:0]+1;int temp=pre[i][j];for(int k=i;k>=0&&temp!=0;--k){temp=fmin(pre[k][j],temp);ans+=temp;}}}return ans;
}