什么是正态分布

正态分布（Normal Distribution，又称常态分布或高斯分布）是统计学中最重要、最常见的一种连续型概率分布，它的概率密度曲线呈经典的“钟形曲线”2。

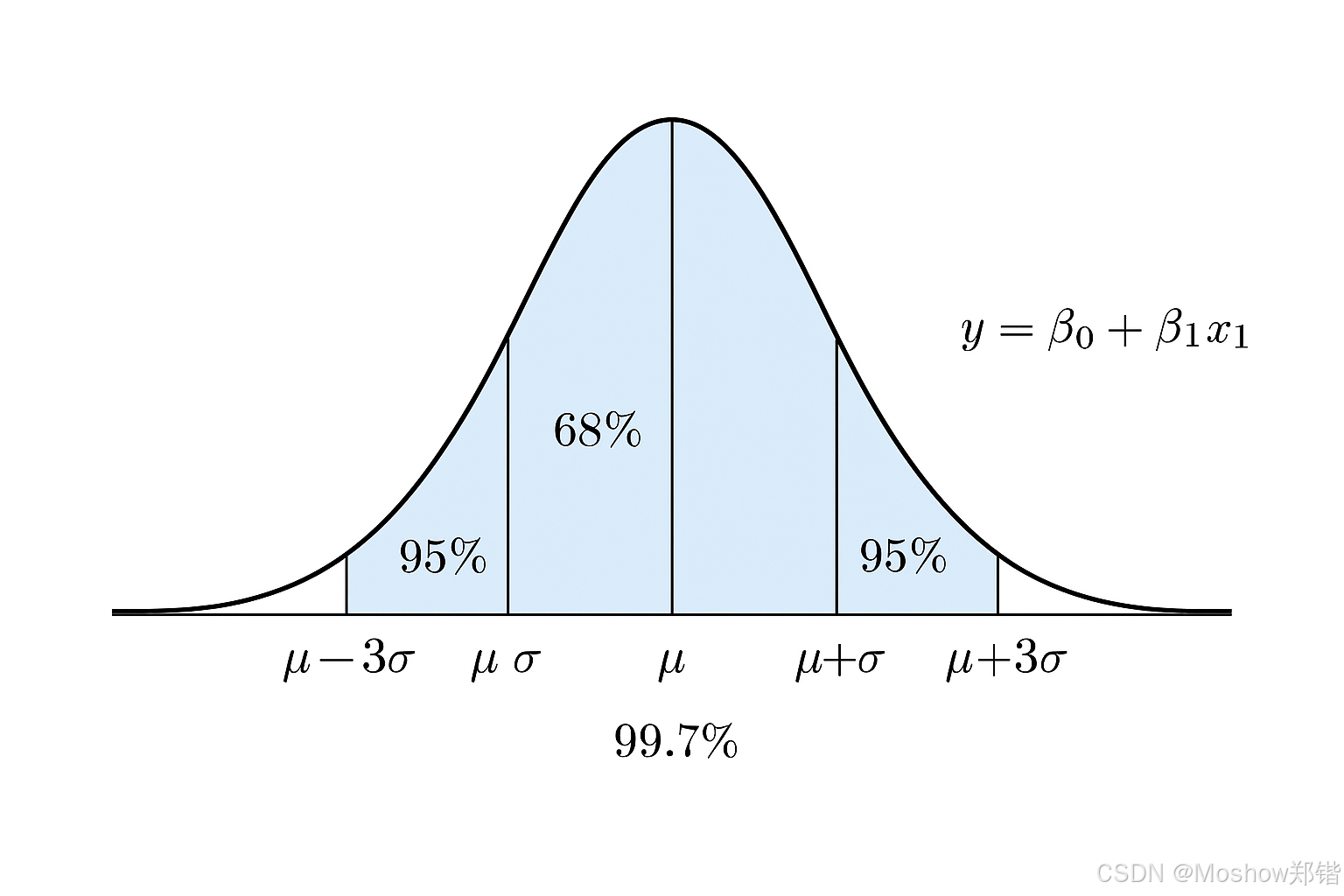
• μ（均值） 在曲线正中，是最高点

• σ（标准差） 决定曲线的宽窄

• 68% 区间：μ ± 1σ（浅蓝色中间部分）

• 95% 区间：μ ± 2σ（中间+两侧第二段）

• 99.7% 区间：μ ± 3σ（几乎覆盖整个曲线）

• 右上角附有正态分布公式

📌 正态分布的核心特征

特征	含义
形状	中间高、两边低，对称分布，曲线在均值处最高
参数	均值 μ（决定曲线位置）、标准差 σ（决定曲线宽窄）
对称性	关于均值 μ 左右完全对称
集中趋势	均值 = 中位数 = 众数
尾部特性	理论上向两端无限延伸但不接触横轴

📐 数学定义

• μ：位置参数，决定曲线中心位置

• σ：尺度参数，决定曲线的陡峭或平坦程度

🎯 68-95-99.7 经验法则

在正态分布中：

• 约 68% 的数据落在 μ ± 1σ 范围内

• 约 95% 的数据落在 μ ± 2σ 范围内

• 约 99.7% 的数据落在 μ ± 3σ 范围内

这也是质量管理中 “六西格玛” 的统计基础。

🔍 为什么它重要？

• 自然与社会现象普遍近似正态分布：如身高、考试成绩、测量误差等3

• 中心极限定理：大量独立随机变量的和趋近于正态分布

• 统计推断基础：很多假设检验、置信区间计算都基于正态分布假设