关于链式二叉树的几道OJ题目
今天笔者带领读者做几道链式二叉树OJ题目,希望读者和笔者一起思考!
1.965. 单值二叉树 - 力扣(LeetCode)

这道题思路不难想,首先知道单值二叉树的定义:所有结点的值都相同,传入的是第一个根节点root,然后考虑几种情况,如果是NULL,那么这是一颗空树,也 满足单值二叉树的要求,所以这种情况直接 返回true,然后考虑整个二叉树,二叉树有左子树,右子树,所以直接比较二叉树一个结点的左右孩子结点即可,如果不等,那就返回false,如果相等,那就继续往下比,下面展示一下笔者写的代码:

2.100. 相同的树 - 力扣(LeetCode)

其实这道题目思路不难想到,无非就是先说特殊情况,然后进行一些递归操作即可:

3.101. 对称二叉树 - 力扣(LeetCode)

还是老规矩,先判断为空,之后为了方便,我们封装一个辅助函数,然后返回的情况其实就很显然了: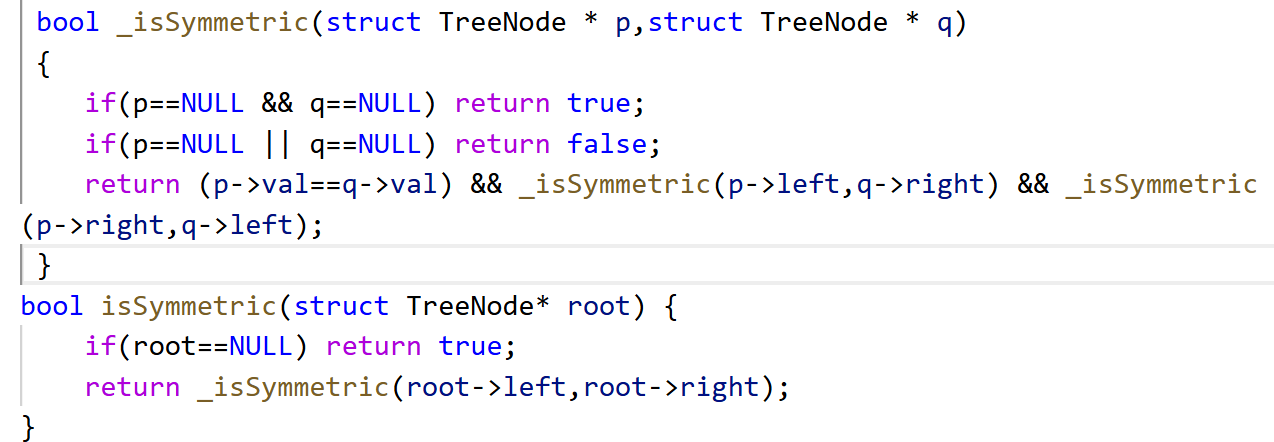
4.144. 二叉树的前序遍历 - 力扣(LeetCode)

由于前序中序后序遍历并无太大 差别,故笔者着重详解一下前序遍历,中序后序留给读者自行练习。这道题首先需要先理解题意,其实意思就是让我们用一个数组存储这个二叉树按照前序遍历的顺序访问的结点,所以观察需要完成的函数,我们需要提供一个returnsize,这其实是由于leetcode的原因,传数组时必须把数组的大小也传进去,也叫输出型参数,综上所述,我们需要单独求出数组的大小,而这这个数组的求法显然需要用malloc函数,创建完数组之后就需要考虑进行前序遍历,下面先给读者看一下笔者的代码:
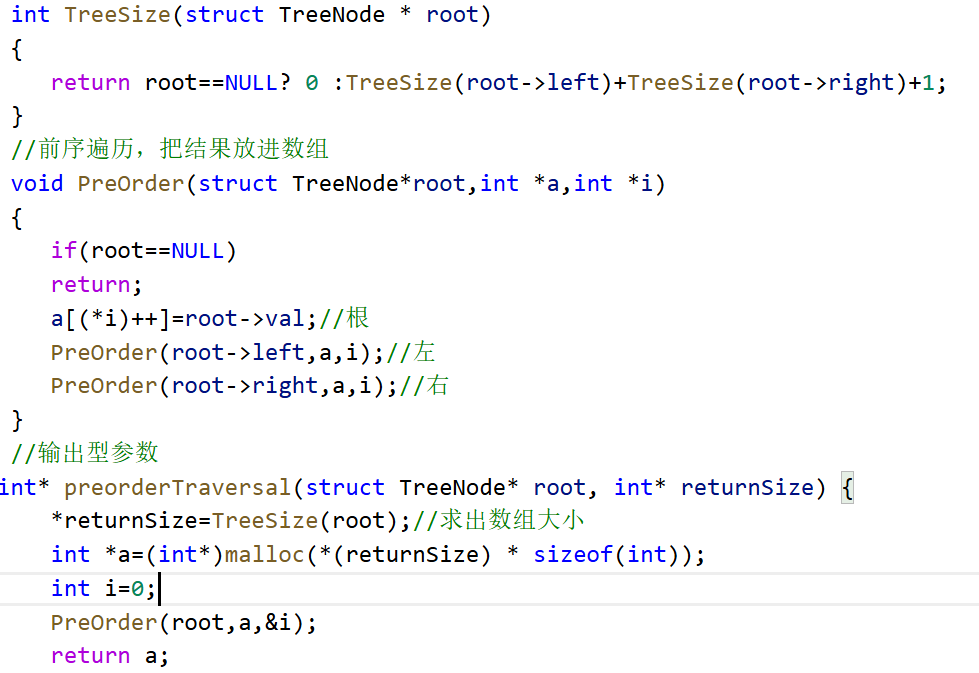
笔者首先求了一个TreeSize,这是因为后面申请内存的时候不会造成浪费,这里需要记住的是returnSize是一个 指针,需要解引用才能当作数组,然后一个很易错的点就是i,相信读者会有 一个问题,为什么i要传入一个指针呢?为什么不能直接传入i呢?其实这个问题在之前的文章中笔者提到过,递归实际上是栈帧问题,通俗理解就是每个副本都会有一个新的i,那些不用的副本中的i始终从1开始,这就会导致混乱,因此需要传入指针,可以理解为传入指针会让根本改变,因为地址找到的东西是固定的,相信到这读者都能理解笔者这么写的原因了。
5.94. 二叉树的中序遍历 - 力扣(LeetCode)
6.145. 二叉树的后序遍历 - 力扣(LeetCode)
7.572. 另一棵树的子树 - 力扣(LeetCode)
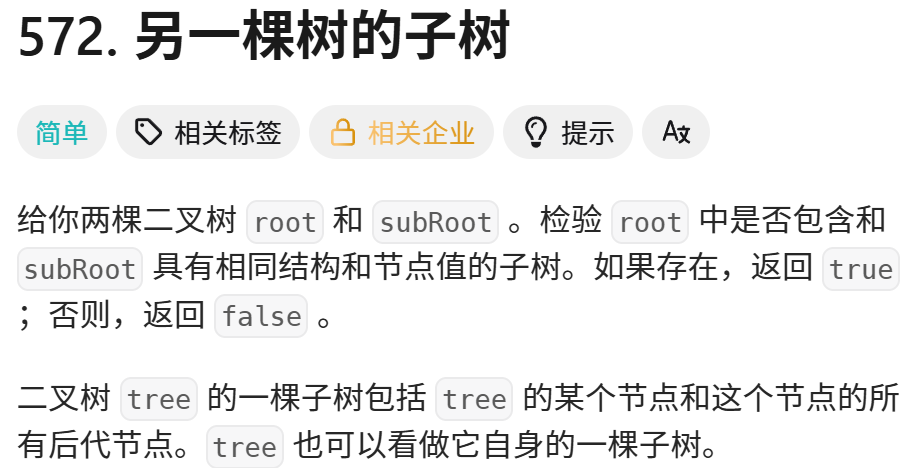
以笔者的习惯,还是先看题目给的函数,传入了两个指针。先判断第一种情况,二者是不是一棵树,如果是一棵树的话那么直接返回true即可,然后就是root为空结点的情况,空结点直接返回false即可,因为空树不可能有子树,然后就是很正常的递归操作了,和之前同理,即可,下面给读者看一下笔者的代码:
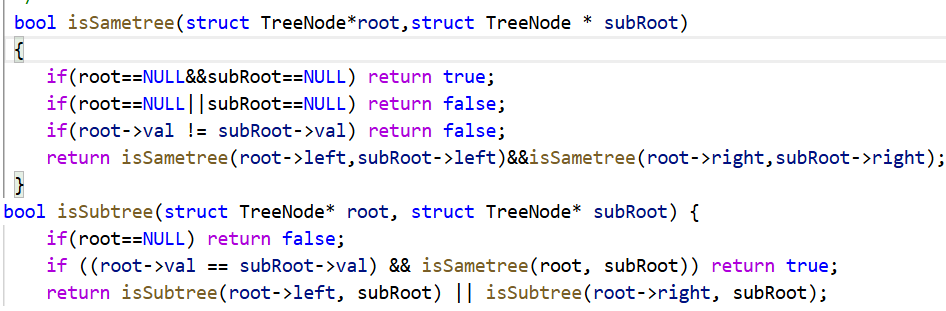
8.二叉树遍历_牛客题霸_牛客网
ok,这就是本文的最后一道题,这道题比较综合,不难理解,这道题的本质是先按照前序创一个二叉树,然后中序遍历,把遍历结果储存起来,其实这道题就是把之前讲过的东西结合在了一起,读者自行完成。
