【深度学习】深度学习中的结构化概率模型：理论、方法与应用

作者选择了由 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 三位大佬撰写的《Deep Learning》(人工智能领域的经典教程，深度学习领域研究生必读教材),开始深度学习领域学习，深入全面的理解深度学习的理论知识。

之前的文章参考下面的链接：
【深度学习】表示学习：深度学习的数据解构与重构艺术
【深度学习】自编码器：数据压缩与特征学习的神经网络引擎
【深度学习】线性因子模型：数据降维与结构解析的数学透镜
【学习笔记】强化学习：实用方法论
【学习笔记】序列建模：递归神经网络（RNN）
【学习笔记】理解深度学习和机器学习的数学基础：数值计算
【学习笔记】理解深度学习的基础：机器学习
【学习笔记】深度学习网络-深度前馈网络（MLP）
【学习笔记】深度学习网络-正则化方法
【学习笔记】深度学习网络-深度模型中的优化
【学习笔记】卷积网络简介及原理探析

1. 引言

在现代人工智能与数据科学领域，概率建模成为推理、决策和数据理解的核心工具。尤为重要的是结构化概率模型，它们通过图形表示变量之间的依赖结构，为理解大规模、高维和复杂关系数据提供了重要解决方案。《深度学习》一书中“图形化模型”章节正是对此类模型的系统阐述，也为深度深度学习模型的设计和分析打下了坚实基础。

---

2. 图形化概率模型简介

结构化概率模型，又称图形化模型（graphical models），是用图结构（nodes为变量，edges为依赖）描述概率分布的一种表示方法。图形化模型可分为两类：

• 有向图模型（Directed Graphical Models），如贝叶斯网络
• 无向图模型（Undirected Graphical Models），如马尔可夫随机场、玻尔兹曼机

图形表示

有向图（贝叶斯网络）示例

考虑三个变量 (A, B, C)，它们两两有依赖关系，可以如下表示：

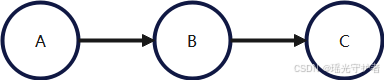
对应的联合分布分解：

$$P(A,B,C)=P(A)P(B|A)P(C|A)$$

无向图（马尔可夫随机场）示例

变量间的边没有方向：

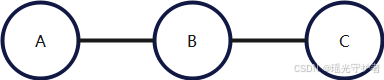
联合分布分解：

$$P(A,B,C)=\frac{1}{Z}{\psi }_1(A,B){\psi }_2(B,C)$$
其中 $$\psi$$ 为势（potential）函数，$$Z$$ 是规范化因子。

---

3. 构造与解释概率图模型

3.1 条件独立性

图的结构清晰呈现出随机变量的条件独立性。如上所示若 $$A\to B\to C$$ 成链，则有

$$P(C|A,B)=P(C|B)$$

即在已知 (B) 的情况下，(C) 与 (A) 条件独立。

3.2 联合分布因式分解

• 有向模型依赖父节点：

$$P(x_1,...,x_n)=\prod _{i=1}^{n}P(x_i|\mathrm{pa}(x_i))$$

其中 $$\mathrm{pa}(x_i)$$ 表示 $$x_i$$ 的父节点。

• 无向模型依赖最大团（clique）：

$$P(x)=\frac{1}{Z}\prod _{C\in \text{cliques}}{\psi }_C(x_C)$$

---

4. 深度学习中的结构化概率模型

深度学习方法与图形化概率模型的结合可归纳为以下几类：

4.1 深度生成模型

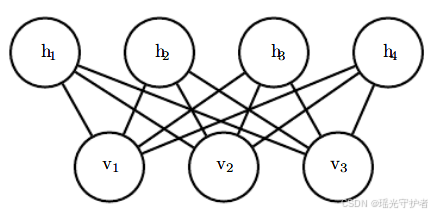
玻尔兹曼机及其深层变体

**玻尔兹曼机（BM）**是一种无向概率模型，能有效捕捉变量之间复杂而对称的依赖关系。

能量函数表示：

$$P(v,h)=\frac{1}{Z}\exp \left(-E(v,h)\right)$$
其中 $$v$$ 为可见层，$$h$$ 为隐藏层。

受限玻尔兹曼机（RBM）：

$$E(v,h)=-a^{T}v-b^{T}h-v^{T}Wh$$

RBM 可扩展至多层深度网络（DBN 或 DBM）。

变分自编码器（VAE）

VAE 结合了概率图模型与神经网络，结构如下：

• 隐变量 $$z$$
• 观测变量 $$x$$
• 联合分布：

$$P(x,z)=P(z)P(x|z)$$

VAE 的推断使用一个近似后验 ( q(z|x) )，用神经网络参数化：

$$\mathcal{L}(\theta ,\varphi ;x)={\mathbb{E}}_{q_{\varphi }(z|x)}[\log p_{\theta }(x|z)]-D_{KL}(q_{\varphi }(z|x)\Vert p(z))$$

变分推断图示

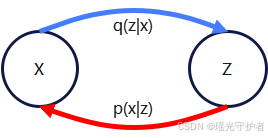
蓝色箭头表示生成路径，红色箭头表示推断路径。

4.2 序列化结构和时序建模

概率图模型擅长处理序列结构，例如：

• 隐马尔可夫模型（HMM）
• 条件随机场（CRF）

对应的概率图结构如下：

联合分布：

$$P(x_{1:T},y_{1:T})=\prod _{t=1}^{T}P(x_t|x_{t-1})P(y_t|x_t)$$

---

5. 推理算法的图结构优势

由于图形化模型明确揭示了独立性，每一步推理可高效分解。例如：

5.1 变量消元（Variable Elimination）

现有如下因子结构：

$$P(A,B,C)=P(A)P(B|A)P(C|B)$$

计算 $$P(C)$$ 时，按图结构顺序消去变量：

$$P(C)=\sum _A\sum _{B}P(A)P(B|A)P(C|B)$$

图结构使高维积分/求和变得可分块管理。

5.2 消息传递算法（Message Passing）

如贝叶斯网络或马尔可夫网络的“信念传播”（Belief Propagation）：

• 逐节点计算边缘概率或最大似然解
• 局部高效、全局协作

---

6. 深度学习与结构化概率模型的融合趋势

6.1 混合模型结构

深度学习允许使用神经网络参数化因子（如条件概率、势函数），结合人工设计的图形结构进行复杂建模。例如：

• VAE 解码器和值编码器用神经网络参数化
• 图神经网络（GNN）在图结构上传递消息，实现端到端学习

公式：

$$f_{\theta }(x_v,x_{ne(v)})$$

其中 $$x_{ne(v)}$$ 表示节点 $$v$$ 的邻居，$$f_{\theta }$$ 为可学习函数。

6.2 端到端训练

现代系统可用反向传播对整个概率图模型进行参数优化，无需手工推断子步骤：

$$\frac{\partial \mathcal{L}}{\partial \theta }=\text{通过自动微分机制进行}$$

---

7. 典型应用场景

• 语音与文本序列建模：HMM+神经网络、序列VAE
• 图数据分析：分子结构、社交网络，常用马尔可夫网络或图神经网络
• 复杂生成任务：图像到文本（Image Captioning）、对抗样本生成等

---

8. 展望：结构化概率模型未来方向

随着算力与数据的增长，概率图模型与深度学习的融合将愈发紧密：

• 高效、大规模推理算法（如变分推断、采样方法）
• 结构可学习，实现自动发现变量依赖关系
• 结合强化学习、因果推断等新兴方法

---

9. 结语

结构化概率模型是连接经典统计推断与现代深度学习的桥梁。通过图结构，我们能够清晰地可视化并组织变量间关系，实现高效数据建模及推理。无论在生成模型、序列数据还是复杂图场景中，它都是不可或缺的基础。随着深度学习的持续发展，这一融合领域将激发更多理论创新与实际应用。