当前位置：首页 > news >正文

【数据结构】选择排序：直接选择与堆排序详解

news 2025/8/23 10:27:34

选择排序

1. 直接选择排序

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

在这里简单优化一下，每遍历一遍，选出最小的数和最大的数，最小的放前面，最大的放后面，这样可以节省一半的遍历次数。

/* 直接选择排序 */
void SelectSort(int* a, int n)
{assert(a);int begin = 0;int end = n - 1;while (begin < end){// 在[begin, end]之间找出最小和最大的数的下标// 分别放在最前面和最后面int mini, maxi;mini = maxi = begin;for (int i = begin + 1; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);// 如果maxi和begin位置重叠，begin与mini交换后maxi的位置需要修正if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);begin++;end--;}
}

直接选择排序的特性总结：

直接选择排序思考非常好理解，但是效率不好。实际中很少使用
时间复杂度：O(N^2)
空间复杂度：O(1)
稳定性：不稳定

2. 堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

2.1 堆向下调整算法

现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提：左右子树必须是小堆，才能调整。

int array[] = {27,15,19,18,28,34,65,49,25,37};

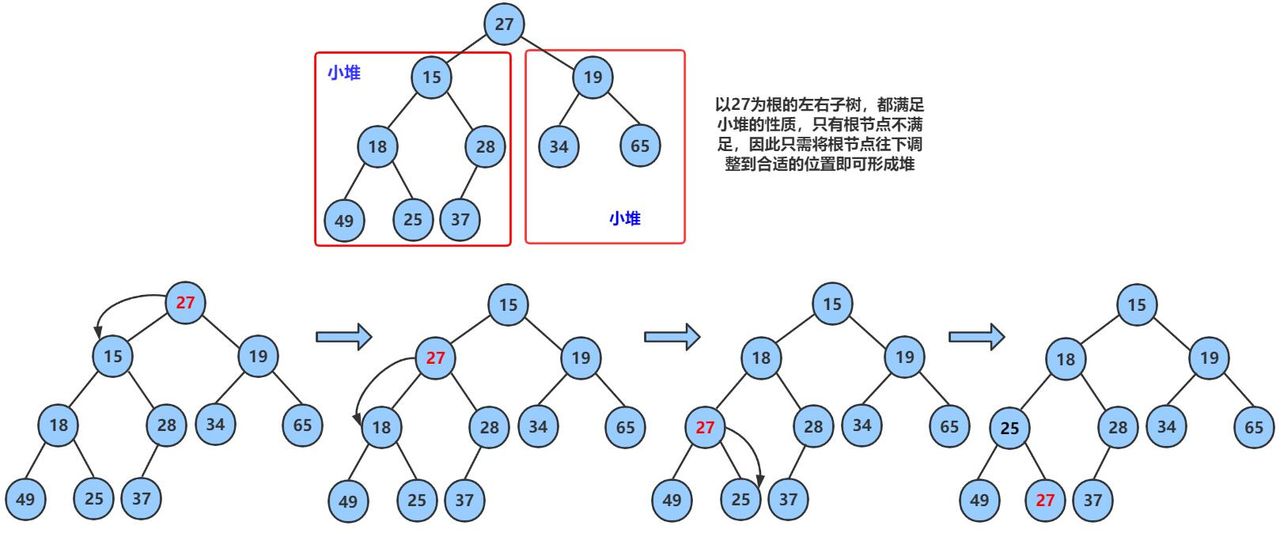
堆向下调整算法就是将根结点与左右两个孩子的最小数比较，如果根结点比左右两个孩子的最小数大，就将左右孩子中最小数结点与根结点互换。然后再将换完位置的根结点与下一层的左右两个孩子进行比较，重复操作，直至根节点比左右两个孩子的最小数还小，则完成调整。

在逻辑上，我们改变的是数的位置，而在实际上，我们改的是数组中的数。

通过完全二叉树的排列规律我们可以知道父子结点的下标关系，从而在数组中精准找到左孩子和右孩子(不了解完全二叉树的性质的去我“二叉树”章节了解)：

父结点下标为n时，左孩子下标为2n+1，右孩子下标为2n+2

通过堆向下调整算法，我们可以将左右子树都为小堆的情况调整为整个堆都符合小堆，那么现在问题来了，我们怎么让左右子树变成小堆呢？答案很简单，当左右子树都只有一个结点时，此时的左右子树既可以看成大堆，也可以看成小堆。

我们只需要从堆的末端开始，从叶子一步一步往根结点实施堆向下调整算法就可以了。（调整顺序如下图所示）

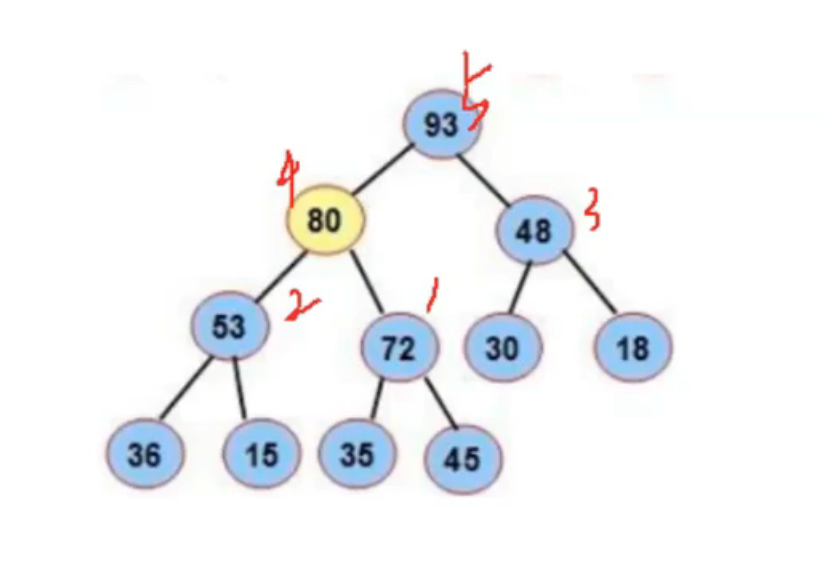
我们已知堆的结点数n（数组元素个数），通过(n-1-1)/2可以得到1号结点的下标，通过下标-1可以得到2、3、4、5号结点的下标，构建循环就可以调整1号根、2号根、3号根...进而调整整个堆结构。

现在我们已经知道了如何将一个给定的数组构建成一个小堆，可以开始写代码了。

2.2 大/小堆构建代码实现

typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap_t;enum HEAP_TYPE
{BIG_HEAP,SMALL_HEAP,
};/* 交换两个变量的值 */
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}/* 堆向下调整算法 */
/* root为根在数组中的下标 */
void AdjustDown(HPDataType* arr, int n, int root, enum HEAP_TYPE heap_type)
{int parent = root;int child = 2 * parent + 1;if (SMALL_HEAP == heap_type){while (child < n){if (child + 1 < n && arr[child] > arr[child + 1])child = child + 1;if (arr[parent] > arr[child]){Swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;}elsebreak;}}else if (BIG_HEAP == heap_type){while (child < n){if (child + 1 < n && arr[child] < arr[child + 1])child = child + 1;if (arr[parent] < arr[child]){Swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;}elsebreak;}}
}/* 将给定的数组初始化为大/小堆 */
void HeapInit(struct Heap* php, HPDataType* a, int n, enum HEAP_TYPE heap_type)
{// 为堆开辟空间php->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);// 可以严谨一点检查malloc是否失败// ...memcpy(php->_a, a, sizeof(HPDataType) * n);php->_size = n;php->_capacity = n;// 构建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->_a, php->_size, i, heap_type);}
}

需要注意，建堆的时间复杂度是O(N)。

2.3 实现堆排序

经过建堆，我们可以得到堆顶是一个最小的数（小堆），但是如何选出次小的数呢？次次小的数？再建堆？明显不能反复建堆，浪费时间。

在堆排序中，排降序：建小堆；排升序，建大堆。通过使用堆的特性，我们可以快速对数组数据进行排序。

排降序时：

建小堆，然后将小堆堆顶的数与堆的最后一个数交换，此时假设堆的长度为n-1(n为原来的数组长度)，再将剩下的堆进行建堆操作，此时除了刚刚换上去的根结点，左右子树都是小堆，所以此时进行堆向下调整算法只用调整“高度”次就可以将整个堆再变为小堆，让此时堆中的最小数再次位于堆顶，然后再将最小数与最后一个数交换，循环操作。

排升序时：

建大堆，剩下的思路与小堆一致。

由于排序时不论堆每一层有多少个结点，都只需要进行一次“两结点交换”操作，使堆排序算法的时间复杂度为O(N*log(2)N)，优于一般的排序算法。

typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap_t;enum HEAP_TYPE
{BIG_HEAP,SMALL_HEAP,
};enum HEAP_SORT_TYPE
{RISE_SORT,DROP_SORT,
};// 堆排序算法实现
void HeapSort(HPDataType* a, int n, enum HEAP_SORT_TYPE heap_sort_type)
{if (DROP_SORT == heap_sort_type){// 1. 建堆// 假设树有n个结点，树高度：log(2)N// 要注意这里时间复杂度不是N*log(2)N，建堆的时间复杂度是O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i, SMALL_HEAP);}// 2.堆排序int end = n - 1;while (end > 0){// 将堆顶与堆底交换Swap(&a[0], &a[end]);// 再继续选次小的AdjustDown(a, end, 0, SMALL_HEAP);end--;}}else if (RISE_SORT == heap_sort_type){// 1. 建堆// 假设树有n个结点，树高度：log(2)N// 要注意这里时间复杂度不是N*log(2)N，建堆的时间复杂度是O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i, BIG_HEAP);}// 2.堆排序int end = n - 1;while (end > 0){// 将堆顶与堆底交换Swap(&a[0], &a[end]);// 再继续选次小的AdjustDown(a, end, 0, BIG_HEAP);end--;}}
}

查看全文

http://www.dtcms.com/a/344907.html