数据结构: 2-3 树的删除操作 (Deletion)
目录
删除的起点
分析删除叶子 key 的两种情况
情况一:叶子节点“很富裕” (The leaf is a 3-node)
情况二:叶子节点“太贫穷” (The leaf is a 2-node)
1️⃣:兄弟节点“很富裕” (Sibling is a 3-node)
2️⃣:兄弟节点也“很贫穷” (Sibling is also a 2-node)
连锁反应 —— 父节点的下溢
根节点的处理 —— 树高的降低
从零开始逐步完善代码
步骤 1: delete 入口和“后继交换”
步骤 2: 核心修复逻辑 fixUnderflow
我们来探讨 2-3 树中与插入操作互为镜像、逻辑同样优雅的操作——删除 (Deletion)。
我们将严格遵循第一性原理,从“删除”这个行为的本质出发,一步步推导出所有必需的代码。
数据结构:2-3 树 (2-3 Tree)-CSDN博客
删除的起点
删除操作必须维持树的两个铁律(节点规则、完美平衡规则)。
从哪里删除最简单?
思考一下,如果我们要删除的 key 位于一个内部节点,会发生什么?
[K2]/ \[K1] [K3]
删除它会留下一个“空洞”,这个空洞下面还挂着两个或三个子树。如何填补这个空洞并重新组织这些子树是一个极其复杂的问题。
[ ] ← 内部节点的 key 被删掉/ \[K1] [K3]
但是,如果我们要删除的 key 位于一个叶子节点,事情就简单多了,因为 K3 没有子树,所以不会产生“空洞 + 悬挂子树”的情况。
内部节点删除:[K2] [ ] (空洞!)/ \ → / \[K1] [K3] [K1] [K3]叶子节点删除:[K2] [K2]/ \ → /[K1] [K3] [K1]
如何将所有删除都转化为“删除叶子节点”?
这个问题在普通二叉搜索树(BST)中已经有了完美的答案,2-3 树借鉴了这个思想:
-
如果要删除的
key就在叶子节点,太好了,直接操作。 -
如果要删除的
key在一个内部节点,我们不直接删除它。取而代之,我们在它的子树中找到一个“替身”来取代它的位置。最合适的替身就是它的中序后继 (in-order successor)——也就是比它大的所有key中最小的那一个。
数据结构:二叉搜索树(BST)的删除操作-CSDN博客
❗关键性质:一个内部节点的中序后继,必然存在于一个叶子节点中。
a. 找到 key 所在内部节点 N。
b. 找到 key 的中序后继 S(它一定在叶子节点里)。
c. 将 S 的值复制到 N 中,覆盖掉要删除的 key。
d. 现在,问题转化成了删除叶子节点中的 S。
✅ 通过“后继交换”的技巧,所有 2-3 树的删除操作,最终都归结为对叶子节点的操作。这是我们整个删除算法的基石。
分析删除叶子 key 的两种情况
当我们定位到要从叶子节点 L 中删除 key 时,根据节点“胖瘦”,有两种情况。
情况一:叶子节点“很富裕” (The leaf is a 3-node)
这是最简单的情况。
-
分析:一个 3-节点有两个
key。拿走一个,它还剩一个,变成一个 2-节点。 -
操作:直接从该节点中移除
key。 -
验证:
-
节点规则:操作后的节点是一个合法的 2-节点。满足。
-
平衡规则:我们只修改了一个叶子,没有改变树高。所有叶子仍在同一层。满足。
-
-
结论:删除操作到此结束。树的平衡没有被破坏。
...│[a | b] ← L 是叶子,有两个 key...│[b] ← L 现在是 2-节点
情况二:叶子节点“太贫穷” (The leaf is a 2-node)
这是 2-3 树删除操作的核心。
一个 2-节点只有一个 key。如果把它拿走,这个节点就空了,变成一个包含 0 个 key 的非法节点。我们称之为下溢 (Underflow)。我们必须立即修复它。
[ P ]/ \[X | Y] [L] ← L 是 2-节点 (只有一个 key Z)[ P ]/ \[X | Y] [ ] ← L 空了,下溢
❓如何修复下溢?—— 向邻居求助
一个节点变“穷”了,自然要向它的兄弟节点(sibling)求助。求助的方式有两种,取决于兄弟的“贫富”。
1️⃣:兄弟节点“很富裕” (Sibling is a 3-node)
如果 L 的左兄弟或右兄弟是一个 3-节点,那么它有多余的 key 可以“借”给我们。但不能直接拿,因为要维持整棵树的搜索顺序。
🔑 再分配 (Redistribution)
这个过程非常像一次“旋转”。 假设“富裕”的兄弟在左边。
-
父节点中,夹在
L和其左兄弟之间的那个key,向下移动到L中。 -
左兄弟节点中最大的那个
key,向上移动到父节点,填补刚刚移走的key的位置。
[ P ]/ \[X | Y] [L] [ Y ]/ \[X] [ P ][ Y ]/ \[X] [P] ← L 重新合法化,成为 2-节点
结果:
-
我们下溢的节点
L从父节点获得一个key,变成了合法的 2-节点。 -
富裕的兄弟节点失去一个
key,变成了合法的 2-节点。 -
父节点只是交换了
key,numKeys不变。 -
整棵树的平衡被局部地恢复了。删除操作结束。
图示:
[ P_k ] [ L_S_k ]/ \ / \[L_S_k | L_L_k] [ ] --> [ L_L_k ] [ P_k ](富裕兄弟) (下溢节点)(P_k 是父节点的 key, L_S_k 是左兄弟的最大 key, L_L_k 是左兄弟的最小 key)
2️⃣:兄弟节点也“很贫穷” (Sibling is also a 2-node)
兄弟自己也只有一个 key,地主家也没有余粮了,无法“再分配”。
[ P ]/ \[A] [L] ← L 是 2-节点 (只有一个 key B)[ P ]/ \[A] [ ] ← L 变空,下溢🔑 合并 (Merging)
既然都这么穷,干脆“合并同类项”,抱团取暖。
-
将父节点中,夹在
L和其兄弟之间的key[P]拉下来 (pull down)。 -
将这个拉下来的
key、兄弟节点的所有key(就一个)、我们下溢节点的所有key(已经空了)合并在一起。 -
这三个部分(我们的空节点、兄弟的 1 个 key、父节点拉下的 1 个 key)将合并成一个新的、合法的 3-节点。
-
同时,删除原来的那个兄弟节点。
[A | P]
结果:
-
在当前层,下溢问题解决了。我们创造了一个合法的 3-节点。
-
但是,这个操作是以从父节点“偷”走一个
key为代价的。
连锁反应 —— 父节点的下溢
⚠️ 合并操作解决了子节点的下溢,但可能导致父节点的下溢。
-
如果父节点在被“偷”走一个
key之后,变成了一个 2-节点(原来是 3-节点),那很好,连锁反应停止。 -
但如果父节点原来就是一个 2-节点,现在被偷走唯一的
key后,父节点自己也下溢了!
❓如何解决? 这个问题和我们刚才解决子节点下溢的问题一模一样,只是场景升高了一层。我们对这个下溢的父节点,应用完全相同的逻辑:
-
检查它的兄弟(我们的“叔叔”节点)是否富裕。
-
如果叔叔富裕,就执行再分配。
-
如果叔叔也贫穷,就执行合并(把父节点、叔叔节点、以及祖父节点的一个
key合并)。
这个下溢的修复过程,可能会像多米诺骨牌一样,从叶子节点一路向上传播。
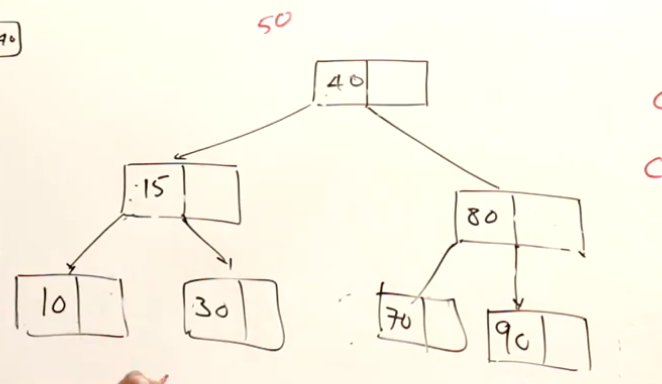
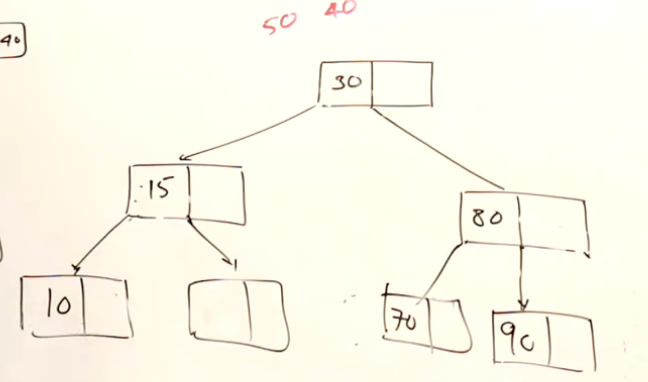
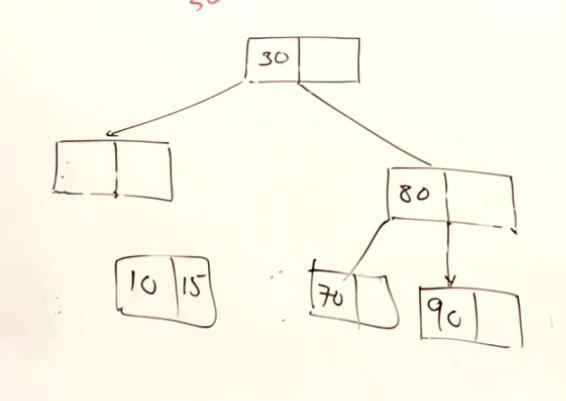
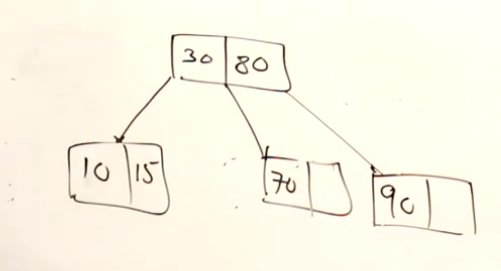
下面的例子中,假设删除20:
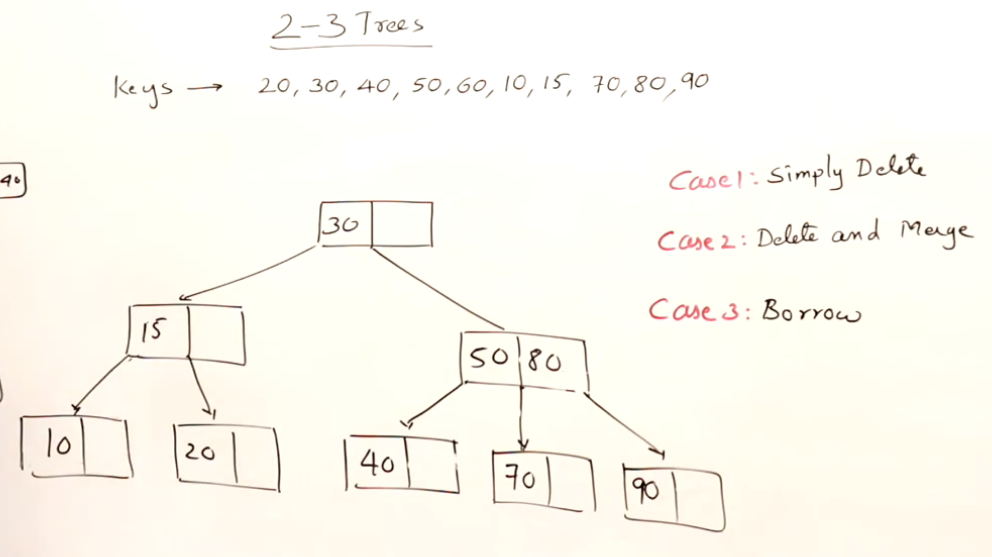
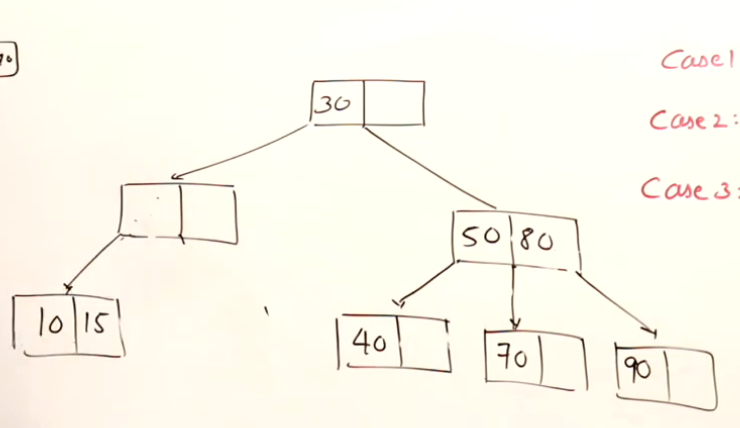
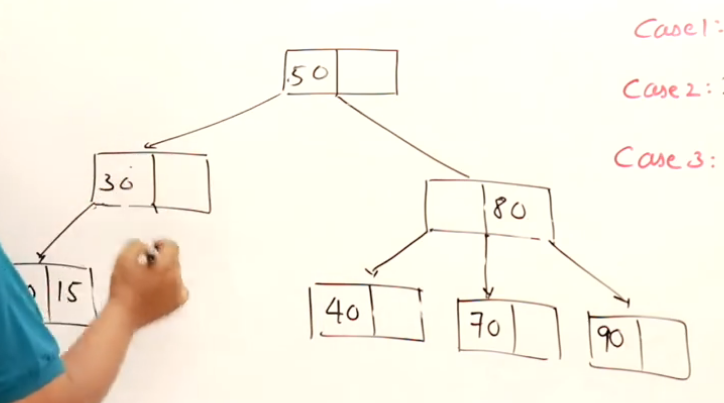
根节点的处理 —— 树高的降低
下溢连锁反应的终点是根节点。
如果下溢一直传播到根节点,会发生什么?
[ P ] ← 根节点,只有一个 key/ \[A] [B] ← 两个 2-节点
假设 [B] 下溢,无法借 key。于是 [A]、P、B 三者合并:
根节点的唯一 key P 被下拉,与左右两个孩子 [A]、[B] 合并成一个新节点:
[ ] ← 根节点变空 (非法)/ \[A] [P] [B][ A | P | B ]
-
这意味着根节点是一个 2-节点(只有 1 个
key)。 -
它的两个孩子执行了合并操作,把根节点唯一的
key也拉了下去。
结果:
-
根节点变空了。
-
它的两个孩子合并成了一个新的、单独的节点。
-
操作:删除空的旧根,让那个合并后的新节点成为新的树根。
[ A | P | B ] ← 新的根
👉 这是 2-3 树高度降低的唯一方式。
当根节点的
key被拉下去参与合并,导致根节点消失时,树的高度-1。这个过程依然保持了所有叶子在同一层,完美平衡规则不被破坏。
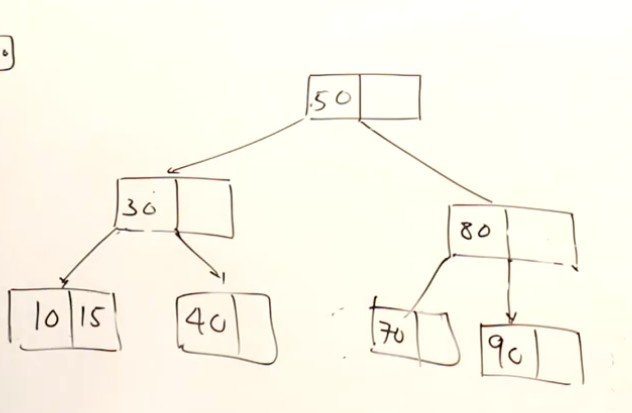
这一次假设删除的节点是40:
从零开始逐步完善代码
我们将从 delete 入口开始,逐步实现上述所有逻辑。
步骤 1: delete 入口和“后继交换”
// 假设已存在上篇文章的 Node 结构和 Tree23 类
// ...
class Tree23 {
private:Node* root;// ... 其他私有函数Node* findNode(int key); // 辅助函数:查找包含key的节点Node* findSuccessor(Node* node, int key); // 辅助函数:找中序后继public:// ...void remove(int key);
};void Tree23::remove(int key) {// 1. 找到包含 key 的节点Node* targetNode = findNode(key);if (targetNode == nullptr) {return; // 树中不存在该 key}// 2. 如果 targetNode 是内部节点,执行“后继交换”if (!targetNode->isLeaf()) {// 找到中序后继所在的叶子节点Node* successorLeaf = findSuccessor(targetNode, key);// 找到后继 keyint successorKey = /* ... find key in successorLeaf ... */;// 交换 key// (省略在 targetNode 和 successorLeaf 中找到并交换 key 的代码)// 更新目标,现在我们要删除的是叶子节点中的后继 keytargetNode = successorLeaf;}// ----------------------------------------------------// 至此,问题已全部转化为:从叶子节点 targetNode 中删除一个 key// ----------------------------------------------------// 3. 从叶子节点中移除 key// (省略从 targetNode->keys 数组中移除 key 并更新 numKeys 的代码)// 4. 检查是否发生下溢if (targetNode->numKeys == 0) {fixUnderflow(targetNode);}
}代码解释:
-
remove函数的第一部分完全遵循我们的推导:将所有删除情况统一为对叶子节点的删除。 -
findNode和findSuccessor是标准的搜索辅助函数,我们在此不展开具体实现。 -
当从叶子节点拿走
key后,我们检查numKeys是否为0。如果是,就调用核心的修复函数fixUnderflow。
步骤 2: 核心修复逻辑 fixUnderflow
这个函数用一个 while 循环来实现向上的连锁反应。
void Tree23::fixUnderflow(Node* node) {Node* currentNode = node;// 循环向上修复,直到当前节点不再下溢,或者到达了根while (currentNode->numKeys == 0 && currentNode != root) {Node* parent = currentNode->parent;// 确定兄弟节点是左是右Node* sibling;int parentKeyIndex; // 父节点中分隔它俩的key的索引// (省略找到 sibling 和 parentKeyIndex 的逻辑)// ...// ===============================================================// 子情况 2a: 兄弟节点“富裕”,执行“再分配”// ===============================================================if (sibling->numKeys > 1) {// (这是非常复杂的指针和key的移动,我们用伪代码表示)// if (sibling is left sibling)// currentNode->keys[0] = parent->keys[parentKeyIndex];// parent->keys[parentKeyIndex] = sibling->keys[sibling->numKeys - 1];// // 如果是内部节点,还要移动孩子指针// ...// else (sibling is right sibling)// ...// 更新 numKeyscurrentNode->numKeys = 1;sibling->numKeys--;return; // 修复完成,退出}// ===============================================================// 子情况 2b: 兄弟节点“贫穷”,执行“合并”// ===============================================================// 合并总是将 parent 的一个 key 拉下来,和两个孩子合并// 我们选择将所有东西合并到左边的节点,然后删除右边的节点Node* leftNode, *rightNode;// (根据 currentNode 和 sibling 的位置确定谁是 leftNode/rightNode)// 1. 将父节点的 key 拉下来leftNode->keys[leftNode->numKeys] = parent->keys[parentKeyIndex];leftNode->numKeys++;// 2. 将右边节点的 key 和 children 移动过来leftNode->keys[leftNode->numKeys] = rightNode->keys[0];leftNode->numKeys++;// (移动 children 指针)// 3. 从父节点中移除被拉下来的 key 和指向右边节点的 child 指针// (这是复杂的数组操作)// 4. 删除右边节点delete rightNode;// 5. 将父节点设为新的当前节点,继续向上检查下溢currentNode = parent;}// -------------------------------------------------------------------// 循环结束,检查根节点// -------------------------------------------------------------------if (root->numKeys == 0) {Node* oldRoot = root;root = root->children[0]; // 合并后的节点成了唯一的孩子if (root != nullptr) {root->parent = nullptr;}delete oldRoot;}
}代码解释:
-
fixUnderflow函数的主体是一个while循环,只要当前节点下溢(numKeys == 0)并且它不是根,循环就继续。 -
再分配 (Redistribution):当
sibling->numKeys > 1时,我们执行这个逻辑。这是一个局部的、常数时间的操作。完成后,整棵树的平衡就恢复了,直接return。 -
合并 (Merging):当
sibling->numKeys == 1时,执行这个逻辑。这个操作会改变父节点的numKeys。因此,循环在结束后,将currentNode指向parent,在下一次迭代中检查父节点是否也因此产生了下溢。 -
根节点处理:当循环结束,意味着我们已经修复到了根,或者下溢没有传播到根。此时需要单独检查根节点。如果根的
numKeys变成了0,说明它的孩子被合并了,并且成为了唯一的孩子children[0]。我们就让这个孩子成为新的根,并删除旧的空根,从而使树的高度降低1。
这个从叶子节点开始,通过“再分配”或“合并”来修复下溢,并可能引发连锁反应直到根节点,最终可能导致树高降低的过程,就是 2-3 树删除操作的完整推导。
