线性回归:机器学习中的基石
在机器学习的众多算法中,线性回归无疑是最基础也是最常被提及的一种。它不仅在统计学中占有重要地位,而且在预测分析和数据建模中也发挥着关键作用。本文将深入探讨线性回归的基本概念、评估指标以及在实际问题中的应用,并通过一个模拟的气象数据集进行数据探索和可视化。
线性回归简介
线性回归是一种通过属性的线性组合来进行预测的线性模型。其核心目标是找到一条直线(在二维空间中)或者一个平面(在三维空间中)甚至更高维的超平面,以此来最小化预测值与真实值之间的误差。
线性模型的一般形式
线性模型的一般形式可以表示为: y=w1x1+w2x2+...+wnxn+b 其中,w1,w2,...,wn 是模型的系数,b 是截距,x1,x2,...,xn 是特征,而 y 是目标变量。
最小二乘法
最小二乘法是求解线性回归模型参数的一种常用方法。它基于均方误差最小化来进行模型求解。具体来说,最小二乘法试图找到一条直线,使得所有样本到这条直线的欧氏距离之和最小。
线性回归的评估指标
评估线性回归模型性能的常用指标包括:
误差平方和/残差平方和 (SSE/RSS):这是预测值与真实值之差的平方和,用于衡量模型的拟合程度。
平方损失/均方误差 (MSE):这是误差平方和的平均值,可以表示为: MSE=n1∑i=1n(yi−y^i)2
R方 (R²):这是决定系数,用于衡量模型对数据的解释能力。R²越接近1,表示模型拟合效果越好。
多元线性回归
当模型包含多个特征时,我们称之为多元线性回归。在这种情况下,模型的求解通常涉及到矩阵运算,以找到最优的系数和截距。
数据探索与可视化
为了更好地理解数据,我们将使用Python进行数据探索和可视化。以下是一个模拟的气象数据集,我们将分析其特征分布、特征相关性、异常值,并进行数据可视化。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns# 假设df是包含数据的DataFrame
df = pd.DataFrame({'气温': np.random.uniform(15, 30, 5000),'湿度': np.random.uniform(40, 80, 5000),'风速': np.random.uniform(2, 10, 5000),'气压': np.random.uniform(1000, 1020, 5000),'目标值': np.random.uniform(15, 30, 5000) + np.random.normal(0, 2, 5000)
})# 1. 数据分布
print("描述性统计:")
print(df.describe())# 2. 特征相关性
print("\n特征相关性:")
print(df.corr())# 3. 异常值检测(以箱线图为例)
plt.figure(figsize=(12, 8))
sns.boxplot(data=df)
plt.xticks(rotation=45)
plt.title('箱线图 - 异常值检测')
plt.show()# 4. 数据可视化
# 散点图矩阵
plt.figure(figsize=(12, 10))
sns.pairplot(df)
plt.suptitle('散点图矩阵', y=1.02)
plt.show()# 气温与目标值的关系
plt.figure(figsize=(8, 6))
sns.scatterplot(x='气温', y='目标值', data=df)
plt.title('气温与目标值的关系')
plt.show()# 湿度与目标值的关系
plt.figure(figsize=(8, 6))
sns.scatterplot(x='湿度', y='目标值', data=df)
plt.title('湿度与目标值的关系')
plt.show()数据分析
数据概览
首先,我们来看一下数据的前几行:
气温:范围从18到22度左右,这是影响目标值(第二天的气温)的主要特征之一。
湿度:大约在60%到80%之间,湿度的范围相对较窄,可能对目标值的影响不如气温明显。
风速:在3到9之间变化,风速的变化范围较大,可能对气温有一定的影响。
气压:在1005到1020 hPa之间,气压的波动范围相对较小。
目标值:第二天的气温,与当天气温有一定的线性关系,但也包含了随机噪声。
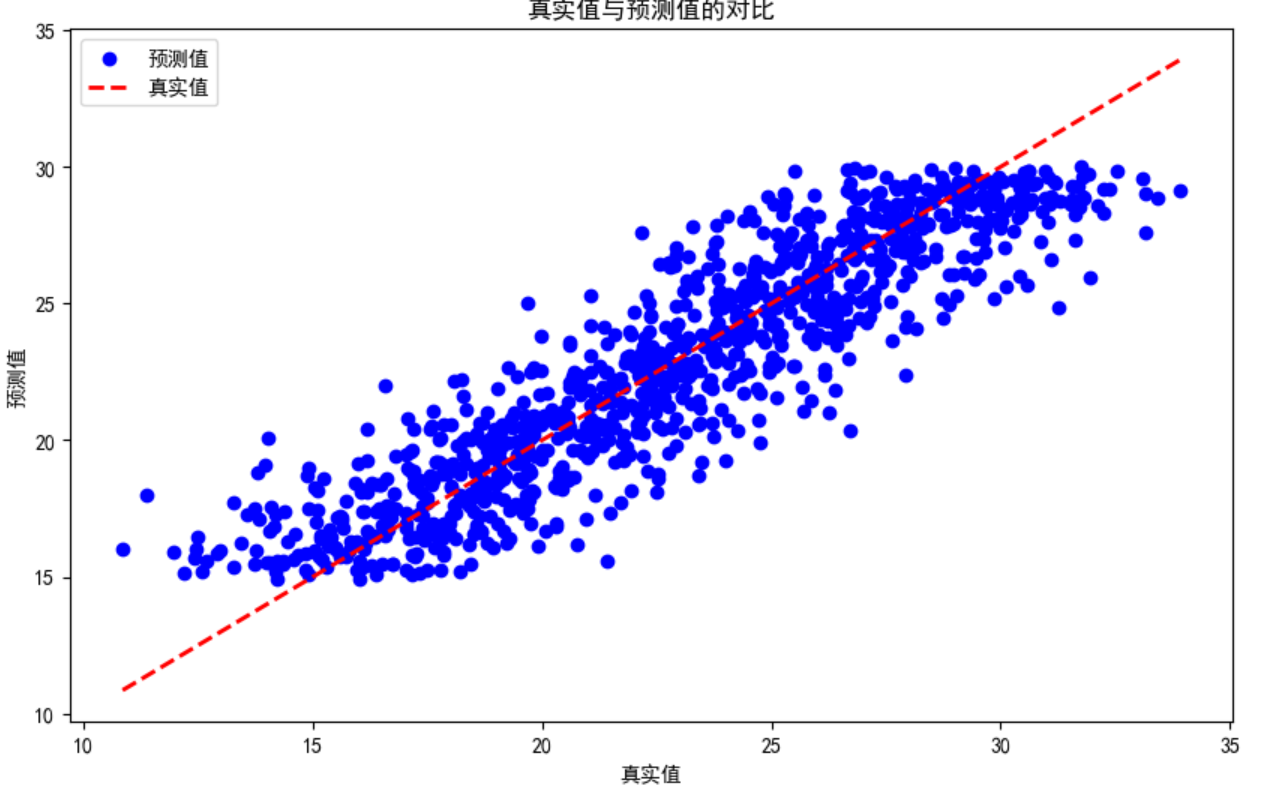
模型评估
均方误差 (MSE): 4.013131461243498
MSE是预测值与实际值之间差异的平方的平均值。较低的MSE值表明模型的预测误差较小,预测结果较为准确。
决定系数 (R²): 0.8211102730112569
R²值衡量的是模型对数据变异性的解释程度。R²值接近1表示模型拟合效果好,能够较好地解释数据的变异性。在这里,0.821表明模型能够解释约82.11%的数据变异性,这是一个相对较高的值,说明模型拟合效果较好。
模型参数
截距 (Intercept): -10.706883157150784
截距表示当所有特征值为0时,模型预测的目标值。在这个气象模型中,截距可能没有实际的物理意义,因为它是一个理论上的值。
系数 (Coefficients): [1.00000805, 5.61622136e-04, 5.65278286e-03, 1.05382308e-02]
这些系数表示每个特征对目标值的影响程度:
气温的系数为1.00000805,表明气温每增加1度,预测的第二天气温平均增加约1.000008度,这是影响目标值的主要因素。
湿度的系数为5.61622136e-04,表明湿度对目标值的影响较小,湿度每增加1%,预测的第二天气温平均增加约0.00056度。
风速的系数为5.65278286e-03,表明风速每增加1单位,预测的第二天气温平均增加约0.00565度,影响相对较小。
气压的系数为1.05382308e-02,表明气压每增加1 hPa,预测的第二天气温平均增加约0.0105度,影响也相对较小。
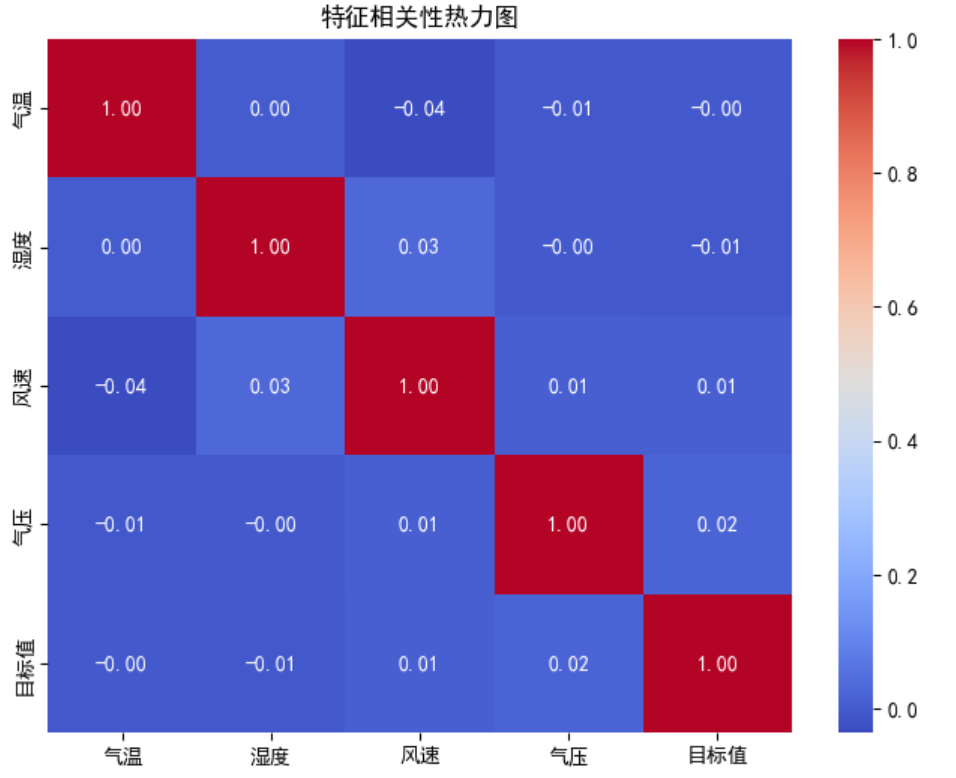
热力图概述
热力图使用颜色来表示数值的大小,通常用于展示矩阵数据。在特征相关性热力图中,颜色的深浅表示特征之间的相关系数的大小,颜色越深表示相关性越强。cmap='coolwarm' 表示使用从蓝色(低相关性)到红色(高相关性)的渐变色。
热力图分析
对角线:热力图的对角线上的值总是1,因为每个特征与自身的相关性是完全相关(即相关系数为1)。
气温与其他特征的相关性:
如果气温的相关系数接近1,颜色接近红色,这表明气温与目标值之间有很强的正相关关系。
如果气温与其他特征(如湿度、风速、气压)的相关系数较低,颜色接近蓝色,这表明气温与这些特征之间的关系较弱。
湿度、风速和气压的相关性:
如果这些特征之间的相关系数较高(接近1),颜色接近红色,这表明它们之间存在较强的线性关系。
如果相关系数较低(接近0),颜色接近蓝色,这表明它们之间的关系较弱。
目标值与其他特征的相关性:
目标值与气温的相关性可能较高,因为气温是影响第二天气温的主要因素。
目标值与湿度、风速和气压的相关性可能较低,这表明这些特征对目标值的影响较小。
实际意义
特征选择:通过分析热力图,我们可以识别出与目标变量相关性较高的特征,这有助于我们在构建模型时进行特征选择。
数据理解:热力图帮助我们更好地理解数据集中特征之间的关系,这对于数据预处理和模型优化非常重要。
异常检测:虽然热力图主要用于展示相关性,但它也可以间接帮助我们识别异常值。例如,如果某个特征与其他特征的相关性异常高或低,这可能是数据异常的迹象。
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('特征相关性热力图')
plt.show()