机器学习-聚类算法
在机器学习的广阔领域中,无监督学习以其独特的魅力占据着重要地位。而在无监督学习的众多算法里,K-means 聚类算法凭借其简洁高效的特点,成为数据挖掘和数据分析领域的常用工具。
一、聚类算法初探:无监督学习的核心
聚类算法是无监督学习的典型代表。在现实场景中,我们常常会遇到没有标签的数据,这时就需要借助聚类算法来发现数据中潜在的结构和模式。简单来说,聚类就是将相似的东西分到一组,让组内的样本尽可能相似,组间的样本尽可能不同。
然而,聚类也面临着不少挑战。其中最主要的难点在于评估聚类结果的好坏以及如何进行参数调优。没有了标签的指引,我们需要依靠特定的评估指标来判断聚类效果,这为聚类任务增添了不少难度。
二、距离度量:聚类的基石
在聚类算法中,距离度量是判断样本相似性的关键。常用的距离度量方法主要有以下两种:
欧式距离
欧式距离也称欧几里得距离,是最常见的距离度量方式,它衡量的是多维空间中两个点之间的绝对距离。在二维空间里,两点(x1,y1)和(x2,y2)之间的欧式距离公式为d=(x1−x2)2+(y1−y2)2;在三维空间中,两点(x1,y1,z1)和(x2,y2,z2)的欧式距离公式为d=(x1−x2)2+(y1−y2)2+(z1−z2)2;推广到 n 维空间,欧式距离公式为d=∑i=1n(x1i−x2i)2,其中x1i和x2i分别表示两个 n 维点的第 i 个坐标。
曼哈顿距离
曼哈顿距离由十九世纪的赫尔曼・闵可夫斯基提出,也被称为出租车几何。它是在几何度量空间中,用于标明两个点在标准坐标系上的绝对轴距总和。在平面上,坐标(x1,y1)的点与坐标(x2,y2)的点之间的曼哈顿距离公式为d(i,j)=∣X1−X2∣+∣Y1−Y2∣。
三、K-means 算法
- 初始化:首先令迭代次数t=0,然后从样本集合中随机选择 k 个样本点作为初始的聚类中心m(0)=(m1(0),m2(0),⋯,mk(0)),其中mi(0)为第 i 个类的初始中心。
- 样本聚类:对于固定的类中心m(t)=(m1(t),m2(t),⋯,mk(t)),计算每个样本到各个类中心的距离,然后将每个样本指派到与其距离最近的中心所在的类中,从而构成聚类结果C(t)。
- 更新类中心:针对得到的聚类结果C(t),计算每个类中所有样本的均值,将这些均值作为新的类中心m(t+1)=(m1(t+1),m2(t+1),⋯,mk(t+1))。
- 收敛判断:检查迭代是否收敛或者是否满足停止条件。如果满足,就输出最终的聚类结果C∗=C(t);否则,令t=t+1,返回步骤 2 继续迭代。
聚类效果评估:CH 指标
如何判断 K-means 聚类的效果呢?CH 指标是一个常用的评估标准。它通过计算类中各点与类中心的距离平方和来度量类内的紧密度,同时通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度。CH 值越大,代表着类自身越紧密,类与类之间越分散,也就意味着聚类结果越优。
K-means 算法的优缺点
优点
K-means 算法具有简单快速的特点,对于常规数据集能够高效地完成聚类任务,在实际应用中有着广泛的使用场景。
缺点
不过,K-means 算法也存在一些不足之处。首先,K 值的确定比较困难,需要结合先验知识或者通过多次试验来选择合适的 K 值;其次,算法的复杂度与样本数量呈线性关系,在处理大规模数据集时可能会面临一定的挑战;另外,它很难发现任意形状的簇,对于非凸形状的数据集聚类效果往往不太理想。
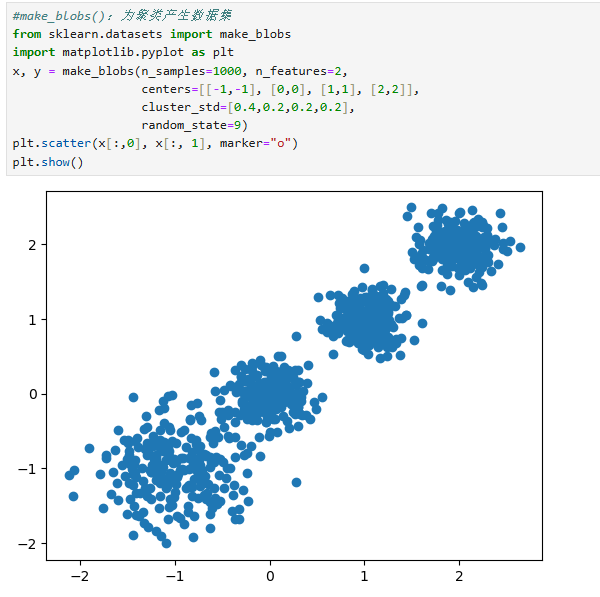
四、数据集生成工具:make_blobs ()
n_samples:数据样本点个数,默认值为 100。n_features:每个样本的特征数,即数据的维度,默认值是 2。centers:表示类别数(标签的种类数),默认值为 3。cluster_std:每个类别的方差。center_box:中心确定之后的数据边界,默认值为(−10.0,10.0)。shuffle:是否将数据进行打乱,默认值是 True。random_state:随机生成器的种子,可以固定生成的数据,保证实验的可重复性。
五、K-means 聚类实现:KMeans ()
n_clusters:分类簇的数量,即我们设定的 K 值。max_iter:最大的迭代次数。n_init:算法的运行次数。random_state:表示随机数生成器的种子,用于保证实验的可重复性。