【无标题】GAP: 用文本指导对任何点云进行高斯化（ICCV 2025）

---

标题：<GAP: Gaussianize Any Point Clouds with Text Guidance>
论文：https://arxiv.org/pdf/2412.01931
来源：南京大学；复旦大学；华为诺亚实验室
主页：https://weiqi-zhang.github.io/GAP.

---

摘要

  三维高斯泼溅（3DGS）在实现快速高效渲染方面展现出显著优势。但是点云作为三维数据表征形式，被广泛应用且易于获取，弥合点云与高斯分布之间的鸿沟变得愈发重要。本文提出GAP，通过文本引导将无颜色点云高效转化为高保真三维高斯泼溅。

  GAP设计了一个多视图优化框架，通过深度感知图像扩散模型实现不同视角下外观的一致性 。为确保几何精度，引入 surface-anchoring机制，在优化过程中约束3DGS始终位于三维形状的表面 。此外，GAP还整合了基于扩散的修复（inpaint）策略，专门针对难以观测区域进行补全 。我们在点云到高斯分布生成任务中对GAP进行了多尺度验证，涵盖从合成点云到复杂真实场景扫描，乃至大规模场景的多种复杂程度

  

二.3DGS初始化

  三维高斯样条（3DGS）[24]是一种现代建模技术，通过一组高斯基元来构建三维形状或场景。每个高斯基元$g_i$由一组参数定义，这些参数表征其几何特征和外观属性。该基元的几何结构在数学上由其中心位置${\sigma }_i\in R^3$和协方差矩阵${\Sigma }_i$共同定义，具体表达式如下：

  协方差矩阵${\Sigma }_i$由旋转矩阵$r_i\in R^4$和缩放矩阵$s_i\in R^3$构成（即${\Sigma }_i=r_i{s}_i{s}_i^T{r}_i^T$）。该矩阵决定了高斯分布的形状、方向及空间范围。除了几何参数外，每个高斯分布还包含视觉属性，例如不透明度参数oi和视图相关色彩特性ci，这些属性均采用球谐函数实现。

  初始化。 将高斯基元的中心位置${\sigma }_i$直接设为输入点云 $P=${$p_i$}${}_{i=1}^N$的空间坐标，其大致呈现底层三维表面特征。为更好利用点云中嵌入的内在几何信息， 采用CAP-UDF方法从点云中学习神经非负距离场（UDF） $f_u$，并通过梯度推理推导出点法线 $N=${$n_i$} ${}_{i=1}^N$：

  采用2DGS作为表征方法：用二维定向的高斯圆盘替代三维高斯椭球体进行场景建模，在呈现局部精细几何结构方面展现出更优性能。2DGS通过圆盘方向直接编码法线信息，利用 场$f_u$中的法线$n_i$为每个高斯样本初始化旋转矩阵$r_i$，确保每个二维高斯圆盘都能精准对齐正确方向，作为好的初始条件。

  

三.多视图修复和更新

  针对序列{$v_j$}${}_{j=1}^k$的每个视角，逐步生成该视角图像$I_j$，以优化相关高斯基元。基于学习到的UDF场，采用ray marching计算逐像素深度图$D_j$。如图2(a)，渲染图像$I_j$，对应深度图$D_j$、mask $M_j$及文本提示$c$，共同输入深度感知修复模型。

  深度感知修复模型(Depth-aware Inpainting Model)：作为外观生成模型，其将深度信息整合到基于扩散的修复过程中，生成更具几何一致性的图像。编码器**$E$的工作流程是：首先将掩膜图像$I$与深度图$D$拼接后输入编码器，生成潜在代码$z_0$**：

  该过程通过一系列加噪操作逐步降解初始的潜在编码。在每个时间步t，模型根据由${\beta }_t$定义的方差调度添加高斯噪声。转换遵循概率分布：

其中$y$是文本嵌入，$g_{\varphi }$是处理图像深度输入的ControlNet。

  为保持生成一致性，每个时间步会有mask blending：时间步 $t$处的潜在编码 $z_t$会根据mask $M$ 与mask区域编码$z_{M,t}$进行结合，来保留unmasked区域的内容：

  Inpainting Updating Scheme：针对修复模型的不确定性（同一区域可能修复出不同的效果），设计了一套动态更新方案：当出现更理想的观察角度时，系统会优化已处理过的区域，即 根据当前视角$v_j$的可见性，将$M$划分为generate mask $M_{generate}$, keep mask $M_{keep}$ 和 update mask $M_{update}$。

  $M_{generate}$表示从未生成的空白区域；$M_{keep}$是已处理过的，且当前视角无法提供更佳的观察条件的区域； $M_{update}$根据视点方向与法线之间的相似度来判断是否刷新的区域。具体们定义了$M_{similarity}$来量化不同视角下表面细节的可观察性。对于视点$v_j$，计算视点方向$d_j$与点法线$N$之间的余弦相似度得出：$M_{similarity}=d_j\cdot N$。当当前视角提供的观察角度，优于其他任何视角时，该区域就需要进行更新：

  最终的修复图$I_{inpaint}$通过两种不同的去噪处理生成的：对newly generated mask采用更强的去噪处理，而对update masks则采用较弱的去噪处理。最终效果的实现方式如下：

  

四.高斯优化

  对于给定视角$v_j$，通过修复模型生成外观$I_j$。高斯分布$G$通过$I_j$进行优化。与传统3DGS拟合方案需要跨多个视角多次迭代优化高斯属性不同， GAP方案每个视角仅需一次优化过程，从而生成更稳健的高斯分布，能够准确呈现高质量外观$I_j$。具体而言，在每个视角专属的优化步骤中，专注于优化当前视角下最近可见表面层对应的高斯分布，而不会修改背面表面的高斯分布（如图3所示）。为此， 高斯选择方案：通过从generate或update mask内的像素出发，沿每条视线射线识别首个相交的高斯分布 。为应对处理大量射线的计算强度，我们开发了利用GPU并行性的CUDA [38]实现方案，将高斯选择过程加速至仅需3秒。

整体损失：

                $L=L_{Rendering}+\alpha L_{Distance}+\beta L_{Scale}$

   Surface-anchoring Mechanism 。在高斯优化过程中，偏离预期表面位置的高斯分布会给多视角修复和模型更新带来重大挑战。这些高斯分布会在后续视角中产生错误的遮挡关系，导致distorted masks，并进一步降低生成和修复的质量。为此，基于距离损失的表面锚定机制，通过将高斯分布与学习到的无符号距离场zero-level set 对齐来实现。具体而言，在优化过程中，我们会约束从$f_u$查询到的每个高斯中心的距离值趋近于零：

   尺度约束 。在从单一视角进行优化时，某些过度放大的高斯函数可能导致几何结构失真，进而影响后续视角的修复效果。尺度约束函数约束每个高斯$s_i$的最大值：

$\tau$是预先定义的阈值，能有效防止高斯过度膨胀，同时仍保留足够的灵活性来模拟外观特征。

   渲染约束 ：

五、基于扩散的未见高斯修复

  如图$2(c)$，为重建未被观测区域的外观特征，提出了一种基于扩散高斯模型的修复方法。如图4所示，该方法能有效恢复最终表征中的缺失外观特征。我们的方案直接在三维空间进行修复操作，充分利用可见高斯分布的内在结构和空间关联性。通过多视角高斯选择方案，我们能够精准识别所有观测角度均未被优化的未观测高斯$G^{\prime }=${$g_j^{\prime }$}${}_{j=1}^M$。对于这些未观测高斯分布，其位置和法向量已通过第3.1节提出的高斯初始化方案完成预设，我们主要关注预测其剩余属性参数，包括颜色、尺度和透明度等关键特征。

  颜色扩散。为预测未见区域的颜色属性，扩散机制通过传播邻近高斯分布的属性来实现。对于每个未见高斯$g_j^{\prime }$，首先确定其最近的L个优化邻近高斯分布作为参考。加权策略：在颜色扩散过程中综合考虑空间邻近性、几何一致性及不透明度可靠性。设$o_{max}$为所有邻近高斯分布中最大的不透明度值。对于未见高斯$g_j^{\prime }$的每个有效邻近高斯$g_j$，其颜色权重${\lambda }_i$计算：当gi与gj′的法线夹角小于60度（即 $n_i\cdot n_j$>0.5）时，权重计算：

否则，权重将被设为0。距离项$1/d_i$可防止外观不一致的远端高斯分布对颜色预测产生显著影响，发现一致项（$n_i\cdot n_j$）通过优先考虑表面方向相似的高斯之间的颜色传播，从而保持几何特征。不透明度可靠项$o_i/o_{max}$确保具有更高不透明度值的高斯分布对颜色预测具有更强的影响力。最后，未见过的高斯$g_j^{\prime }$的颜色$c_j^{\prime }$可表示为：

  Size Scale.采用最近邻法（包括已优化和未见过的高斯）预测未见过的高斯分布$g_j^{\prime }$的合适尺度：根据这些邻近点的空间距离进行调整。未见的高斯分布的尺度$s_j^{\prime }$计算公式：

其中d表示未观测到的高斯分布gj′与其邻近分布gi之间的距离。我们引入了距离加权机制，因为较大的距离对应着需要更大尺度的稀疏区域。

  Opacity Control.在预测未知高斯分布gj′的不透明度o′j时，我们采用基于密度的控制机制。半径ρ内的不透明度与局部高斯密度成反比。未知高斯分布$g_j^{\prime }$的不透明度$o_j^{\prime }$计算公式如下：

其中，$o_0$是base不透明度值，P表示指定半径ρ内的高斯分布密度数量，P0为参考密度阈值。该不透明度控制方案通过降低高斯分布密度较高的区域不透明度值，既避免颜色过度堆积，又能确保表面覆盖度达标。

实验

1.文本驱动外观生成

  数据集与指标。在Objaverse [12]数据集的子集：包含225个类别的410个纹理模型，仅使用10万点的采样点云作为输入。采用三种互补评估指标：弗雷歇-Inception距离（FID）[58]和核Inception距离(KID×10−3）[3]用于图像质量评估，CLIP分数[41]用于文本-图像对齐度量。所有方法均采用相同的文本提示描述每个物体。所有物体均从固定视角以1024×1024像素的高分辨率进行渲染。

  基线。在视觉效果方面，GAP对比的其他三维纹理生成方法：基于UV贴图的TexTure [42]、Text2Tex [7]、Paint3D [60]和SyncMVD [30]。这些方法均采用UV贴图技术。而Objaverse数据集子集中的原始网格包含艺术家创作的UV贴图。为确保在相同点云输入条件下公平比较，我们使用传统球枢算法（BPA）[2]和前沿学习方法CAP-UDF [68]从输入点云重建网格，并通过xatlas [56]unwrap生成UV贴图。

  

定量比较见表1，GAP采用高斯样条技术实现了本质上的更高渲染质量，优于使用重建网格的基准方法（存在拓扑结构模糊、连接错误和几何畸变等问题）。gap通过直接优化三维空间中的高斯基元来绕过UV参数化。如图5所示，虽然现有方法能生成看似合理的外观效果，但在细节保留方面存在明显短板。通过在三维空间中直接优化外观表现，gap在各类物体上均展现出更优的视觉品质。

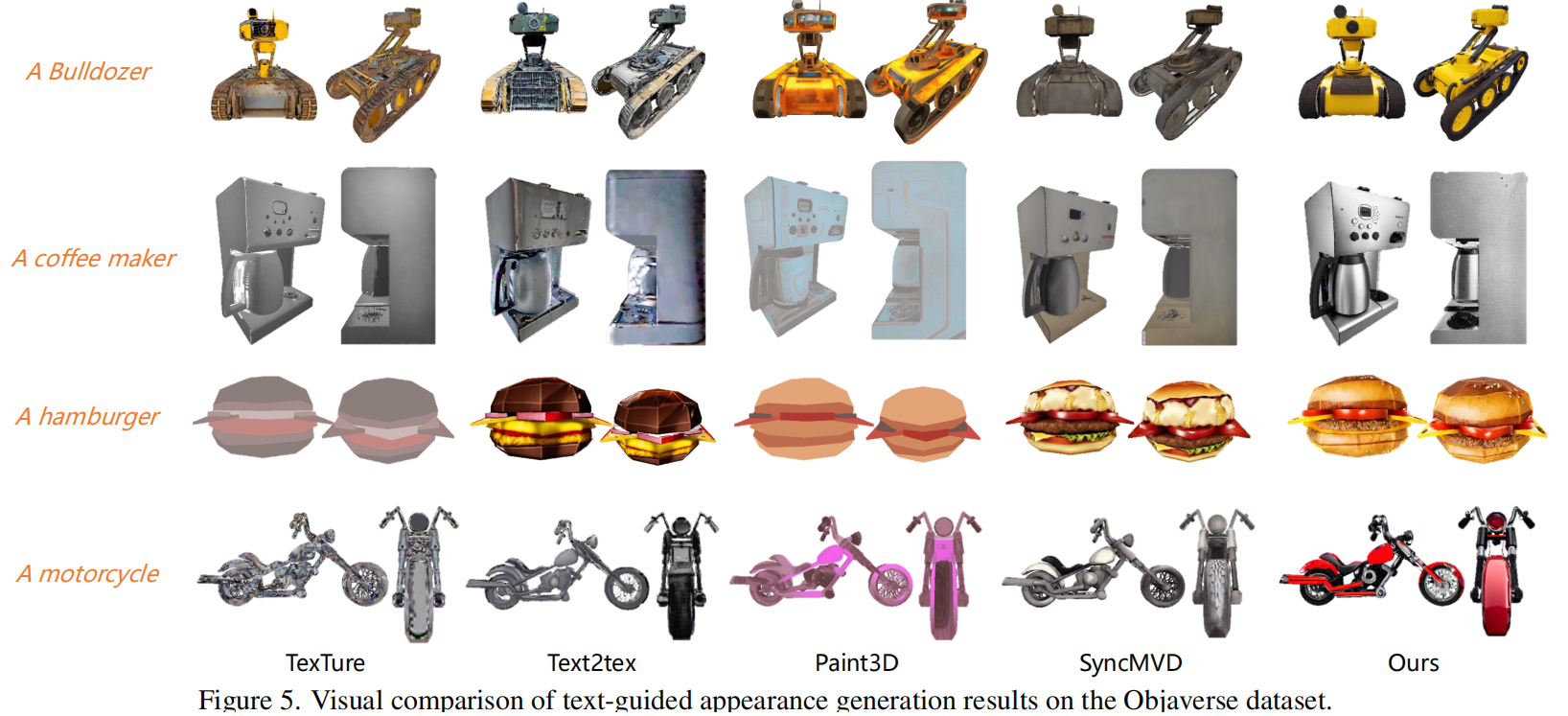
为了评估视觉外观和文本对齐，我们进行了一个有30名参与者的研究。每个参与者都独立地从多个角度评估了所有方法的结果，并根据1到5的评分标准进行打分.

  

2.点云到高斯的生成

  为评估GAP在点到高斯生成中的有效性，在两个数据集上开展实验：ShapeNet椅子类别[6]和DeepFashion3D [81]。我们从每个3D模型中均匀采样10万个点来生成输入点云。GAP与三种前沿方法DreamGaussian [47]、TriplaneGaussian [82]和DiffGS [76]进行对比，所有方法均使用相同的10万点云作为输入。

  图6展示了与基线方法的视觉对比。相较于现有方法，GAP始终能生成更具视觉吸引力且几何精度更高的结果。基线方法存在若干关键缺陷：DreamGaussian虽然采用了评分蒸馏采样（SDS）进行外观优化，但容易产生色彩不自然的过度饱和效果；其优化过程不仅计算量大，还对参数高度敏感。TriplaneGaussian和DiffGS则因受限于低分辨率三平面表征，难以有效捕捉外观细节。

  

3.扫描输入的高斯生成

  数据集。在来自SRB（Scan-to-Reality Benchmark）[50]和DeepFashion3D [81]的真实场景部分扫描数据集上评估GAP方法。这两个数据集均包含深度传感器采集的点云数据，存在覆盖不全、遮挡及扫描伪影等现实场景挑战。我们直接采用原始扫描点云作为输入。性能表现。如图8所示，GAP成功将部分点云进行高斯化处理，生成完整且高质量的高斯表示。我们的表面锚定机制能有效拉伸分割和克隆的三维高斯分布，填补缺失区域的同时保持几何一致性。实验结果表明，该方法能够稳健处理真实场景扫描点云中的伪影与遮挡问题，并生成视觉效果出众的高斯分布模型。

  

4.场景级高斯生成

  数据集。我们在合成场景（3DFRONT [14]，室内环境）和真实场景（[Dense Scene Reconstruction with Points of Interest，2013]，具有拓扑结构复杂、点密度变化及扫描伪影等挑战）数据集上对GAP进行评估。我们从场景网格中采样50万个点作为输入。

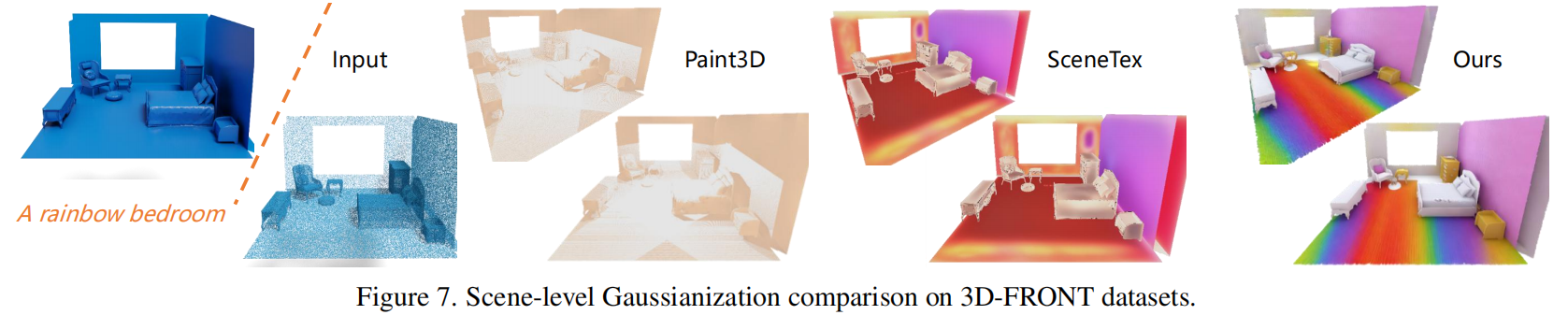
  与Paint3D [60]和Scenetex [8]相比，我们的方法在视觉质量上表现更胜一筹，如图7，Paint3D在场景级数据处理中表现欠佳，而Scenetex不仅需要进行VSD优化[48]，还需额外进行LoRA [20]训练，导致处理时间大幅增加。相比之下，我们的方法仅需一次优化过程即可在复杂场景中输出高质量结果。

  

#pic_center =80%x80%

$\sqrt{d}$ $\frac{1}{8}$ $\bar{x}$ $\hat{D}$ $\tilde{I}$ $ϵ$
$\varphi$ $\prod$ $\sqrt{abc}$ $\sum abc$
/ $$