3D检测笔记：相机模型与坐标变换

前言

 激光雷达检测到的点是三维点，在多模态融合时，将三维的坐标点映射到二维成像平面上以此实现点云数据与图像数据的融合，这个操作是很常见的。

相机模型介绍

 在这篇博客中介绍了激光雷达坐标系、相机坐标系、以及图像坐标系三者。各坐标系的定义如下：

 相机模型讲的就是从相机坐标系到图像坐标系的映射，也就是我们常说的小孔成像模型：

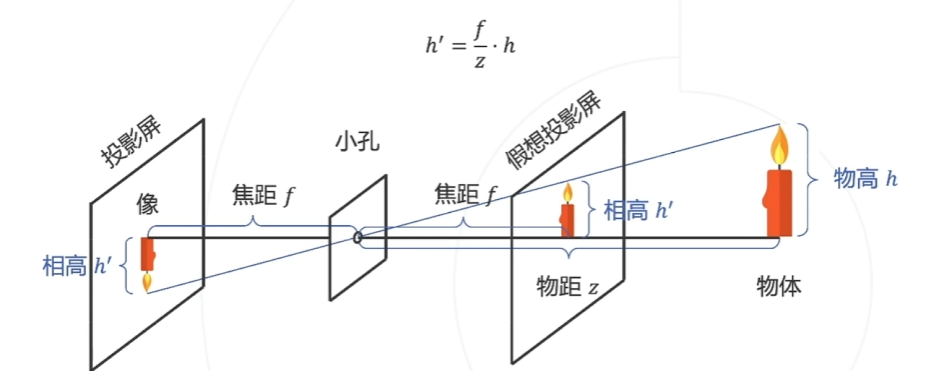
 这个图要怎么理解呢？我们令中间这一条线为主光轴，它与所有平面的交点为原点。那么可以清晰地看到：物高为h的蜡烛在成像平面上的相高h’为焦距f除以物距z，所以如果相机坐标系和图像坐标系原点重合，并且u对应x轴，v对应y轴的话。会有如下关系(相似三角形)：
$$\begin{gathered} u=Xc\times \frac{fx}{Z} \\ v=Yc\times \frac{fy}{Z} \end{gathered}$$

世界坐标系到相机坐标系

 由前面对坐标系的学习可以知道：世界坐标系与相机坐标系都是右手系，并且同一手系之间的变换都是刚性的（即由旋转和平移组成）。

平移的本质

$$\left[\begin{array}{c}Xc\\ Yc\\ Zc\end{array}\right]=\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]+\left[\begin{array}{c}tx\\ ty\\ tz\end{array}\right]$$
 平移的本质相当于原坐标加上一个偏移矩阵。也可以用矩阵乘法来表示：
$$\begin{array}{r}\left[\begin{array}{c}{X}_c\\ Y_c\\ Zc\\ 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]\end{array}$$

旋转的本质

 旋转的本质是旋转矩阵乘以坐标点。例如下面的例子：

 这是坐标系绕Z轴旋转的例子。可以列出式子：
$$\begin{array}{rlr}\cos b=\frac{x}{op}& & \sin b=\frac{y}{op}\\ \cos (b-a)=\frac{x_c}{op}& & \sin (b-a)=\frac{y_c}{op}\end{array}$$
展开（2）可得：
$$\begin{array}{r}{x}_c=\cos a\times x+\sin a\times y\\ y_c=-\sin a\times x+\cos a\times y\\ \left[\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}\right]=\left[\begin{array}{ccc}\cos a& \sin a& 0\\ -\sin a& \cos a& 0\\ 0& 0& 1\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\end{array}\right]\end{array}$$
其中：
$$R_z=\left[\begin{array}{ccc}\cos a& \sin a& 0\\ -\sin a& \cos a& 0\\ 0& 0& 1\end{array}\right]$$
Rz为坐标系绕z轴旋转的旋转矩阵，同理还有Rx,Ry。那么坐标系旋转的本质就相当于旋转矩阵乘以原坐标。旋转矩阵R为：
$$R=R_z\times R_y\times R_x$$
（一般旋转顺序为z->y->x，旋转顺序不同，变换的结果也不同）

变换的本质

 在坐标系变换中，先平移后旋转和先旋转后平移的坐标变换是不同的，我们在这里规定标准的变换是‌先旋转后平移‌。
那么从世界坐标系到相机坐标系的变换用式子来表示即为：
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{33}& T_{31}\\ 0& 1\end{array}\right]\times \left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$
其中：
$$\left[\begin{array}{cc}{R}_{33}& T_{31}\\ 0& 1\end{array}\right]$$
称为外参矩阵。
外参矩阵可逆，取逆时表示从相机坐标系到世界坐标系的变换。

相机坐标系到图像坐标系

 在前面相机模型那部分我们推导出：
$$\begin{gathered} u=Xc\times \frac{fx}{Z} \\ v=Yc\times \frac{fy}{Z} \end{gathered}$$
但实际上相机坐标系是以以镜头主光轴中心为原点，也就是说相机坐标系的Z轴是垂直穿过图像坐标系中心（Cx,Cy）的。
 设W，H是图像的宽于高，那么就有：
$$\begin{gathered} u=Xc\times \frac{fx}{Z}+\frac{W}{2} \\ v=Yc\times \frac{fy}{Z}+\frac{H}{2} \end{gathered}$$
用矩阵乘法表示就是：
$$\begin{array}{r}{Z}_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]\end{array}$$
其中K为内参矩阵，表达式如下：
$$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$
其中，fx，fy代表相机在x,y方向上的焦距，Cx,Cy代表图像宽和高的一半。