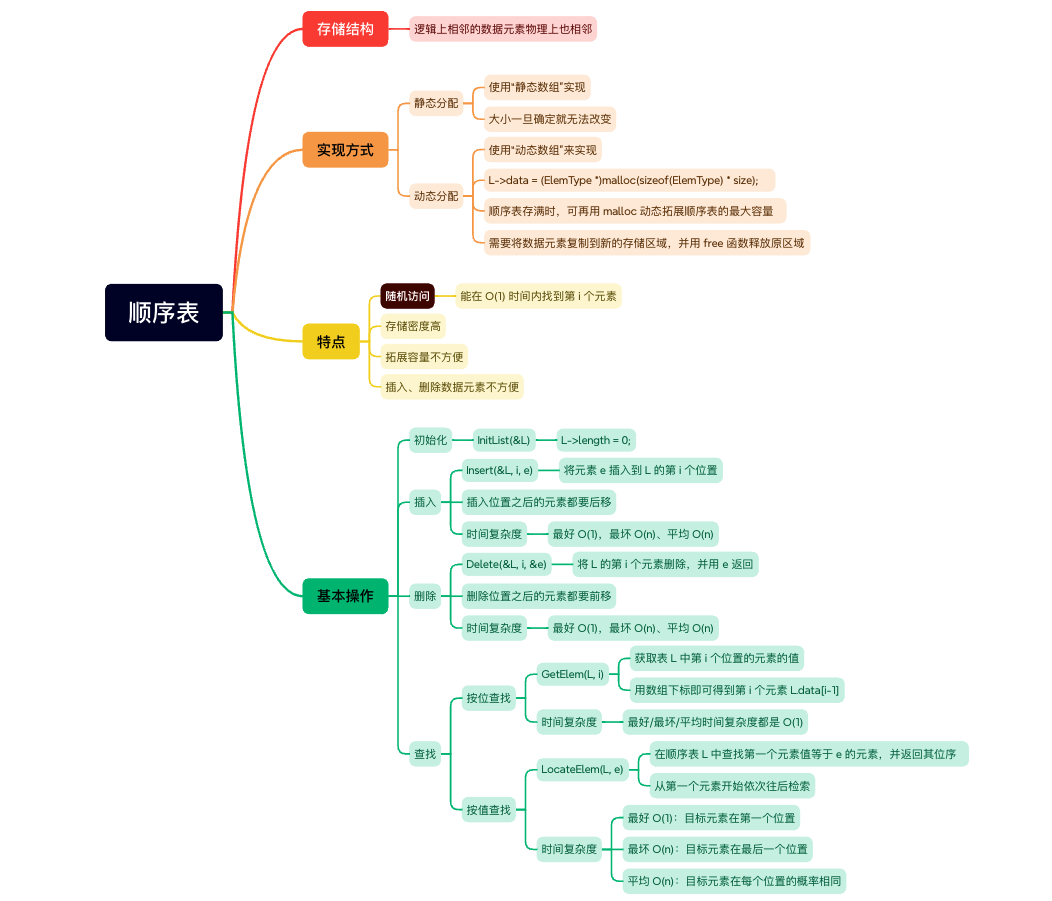
【数据结构】线性表——顺序表
目录
- 线性表
- 线性表的定义
- 顺序表
- 顺序表的定义
- 顺序表的初始化
- 静态分配
- 动态分配
- 顺序表的插入
- 顺序表的删除
- 顺序表的查找
- 按位查找
- 按值查找
- 代码实现
- 总结
线性表
线性表的定义
定义:线性表(Linear List) 是一种数据结构,它是 n 个具有相同类型的数据元素的有限序列。
若把元素记为 a1,a2,…,ana_1,a_2,…,a_na1,a2,…,an,满足:
- 除第一个元素外,每个元素有且仅有一个直接前驱;
- 除最后一个元素外,每个元素有且仅有一个直接后继;
- 线性结构,逻辑次序是线性的。
典型基本操作(抽象接口,后面不同实现会给出具体代码):
InitList(&L):初始化表。构造一个空的线性表 L,分配内存空间DestroyList(&L):销毁操作。销毁线性表,并释放线性表 L 所占用的内存空间ListInsert(&L, i, e):插入操作。在表 L 中的第 i 个位置上插入指定元素 eListDelete(&L, i, &e):删除操作。删除表 L 中第 i 个位置的元素,并用 e 返回删除元素的值LocateElem(L, e):按值查找操作。在表 L 中查找具有给定关键字值的元素GetElem(&L, i):按位查找操作。获取表 L 中第 i 个位置的元素的值ListLength(L):求表长。返回线性表 L 的长度,即 L 中数据元素的个数PrintList(L):输出操作。按前后顺序输出线性表 L 中的所有元素值ListEmpty(L):判空操作。若 L 为空表,则返回 true,否则返回 false
顺序表
顺序表的定义
定义:顺序表(Sequential List)是一种线性表的顺序存储结构,它使用一段连续的存储单元来依次存放线性表中的元素。
特点:
- 逻辑上相邻的元素,在物理上也相邻。
- 支持随机存取,可以通过下标直接访问任意元素。
- 插入和删除操作需要移动元素,效率较低(平均要移动一半元素)。
适用场景:适合数据量相对固定、查找操作频繁的场景。
顺序表的存储结构:
- 使用数组保存数据元素。
- 需要一个变量记录顺序表当前长度(元素个数)。
- 通常还需要一个变量记录顺序表的最大容量(数组大小)。
顺序表的初始化
静态分配
- 在内存中分配存储顺序表 L 的空间。包括
MAXSIZE*sizeof(ElemType)和存储length的空间 - 将各个数据元素的值设为默认值(可省略,后面会讲述原因)
- 将
length的值设为 0
原理:在定义顺序表时,就用固定大小的数组分配存储空间。
特点:
- 大小在编译时确定,运行期间不可改变。
- 空间利用率可能不高,要么浪费内存,要么不够用。
- 优点是实现简单,访问效率高。
C 语言演示代码如下:
#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 10typedef struct {int data[MAXSIZE]; // 存放元素的静态数组int length; // 当前表的长度
} SeqList;// 顺序表初始化实现
void InitList(SeqList *L) {for(int i=0; i<MAXSIZE; i++)L->data[i]=0; // 将所有数据元素设置为默认初始值L->length = 0; // 通过指针L访问顺序表的length成员,将其赋值为0。
}int main() {SeqList L; // 声明一个顺序表InitList(&L); // 初始化顺序表return 0;
}
输出一下结果:
printf("顺序表元素: \n");
for (int i = 0; i < MAXSIZE; i++) {printf("data[%d]=%d\n", i, L.data[i]);
}
结果如下:

假如在初始化操作中不将所有数据元素设置为默认初始值
void InitList(SeqList *L) {L->length = 0;
}
输出的结果则大不相同:
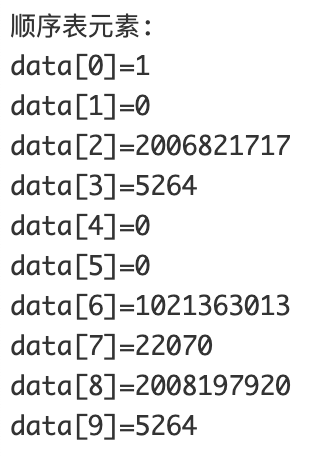
造成这样的原因是内存中存在脏数据,也就是说读取到了内存中未初始化的残留值,但是前面说过是可以省略初始化默认值的,这是因为打印数组如果直接用 i<MAXSIZE 是违规的,而且如果 MAXSIZE 的值很大,还会造成初始化时间过长,内存浪费。正确的方法应该是用 i<L.length 通过顺序表的长度来访问数据元素,这样才是合规的,才能避免读取到内存中的脏数据。
顺序表初始化的代码如下所示:
#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 10typedef struct {int data[MAXSIZE]; // 存放元素的静态数组int length; // 当前表的长度
} SeqList;// 顺序表初始化实现
void InitList(SeqList *L) {L->length = 0; // 通过指针L访问顺序表的length成员,将其赋值为0。
}int main() {SeqList L; // 声明一个顺序表InitList(&L); // 初始化顺序表printf("顺序表元素: \n");for (int i = 0; i < L.length; i++) {printf("data[%d]=%d\n", i, L.data[i]);}return 0;
}
静态分配的局限性: 顺序表容量不可变,存满后无法扩展;若初始申请过大空间,可能浪费内存资源。
动态分配
原理:在运行时根据需要,动态申请存储空间(用 malloc 或 calloc ),数组大小可以灵活设定。
-
传统方法:
malloc+free- 定义动态顺序表
// 定义动态顺序表结构体 typedef struct {int *data; // 动态分配数组的指针int MaxSize; // 顺序表最大容量int length; // 顺序表现有长度 } SeqList; - 用
malloc申请一片连续的内存空间,并初始化// 初始化顺序表 void InitList(SeqList *L) {// 分配内存:InitSize 个 int 大小的空间L->data = (int *)malloc(InitSize * sizeof(int));if (L->data == NULL) { // 检查内存分配是否失败printf("内存分配失败!\n");exit(1); // 直接终止程序(也可返回错误码处理)}L->length = 0; // 初始化为空表L->MaxSize = InitSize; // 设置初始最大容量 } - 增加动态数组长度
// 扩容函数:将最大容量增加 len void IncreaseSize(SeqList *L, int len) {int *p = L->data; // 保存原数据的地址(用于释放和拷贝)// 分配新内存:原容量 + lenL->data = (int *)malloc((L->MaxSize + len) * sizeof(int));if (L->data == NULL) {printf("内存扩容失败!\n");exit(1);}// 拷贝原有数据到新内存for (int i = 0; i < L->length; i++) {L->data[i] = p[i];}L->MaxSize += len; // 更新最大容量free(p); // 释放原内存(避免内存泄漏) } - main 函数中执行方法
int main() {SeqList L; // 声明顺序表变量InitList(&L); // 初始化(传地址,因为函数参数是指针)// 手动插入几个元素(演示用,实际可封装插入函数)for (int i = 0; i < 5; i++) {if (L.length < L.MaxSize) { // 确保不超出容量L.data[L.length++] = i; // 插入数据并更新长度}}printf("扩容前:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 扩容:最大容量增加 5IncreaseSize(&L, 5);printf("扩容后:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 释放动态分配的内存(必须!否则内存泄漏)free(L.data);return 0; } - 核心逻辑说明
- 动态分配:通过
malloc申请堆内存,避免栈内存大小固定的限制; - 扩容流程:
- 保存原数据指针
p; - 分配更大的新内存;
- 拷贝原数据到新内存;
- 更新容量并释放原内存;
- 保存原数据指针
- 使用后释放:动态分配的内存需手动
free,否则程序结束前不会自动回收。
- 动态分配:通过
完整代码如下:
#include <stdio.h> #include <stdlib.h> // 包含 malloc、free 等函数#define InitSize 10 // 默认最大长度// 定义动态顺序表结构体 typedef struct {int *data; // 动态分配数组的指针int MaxSize; // 顺序表最大容量int length; // 顺序表现有长度 } SeqList;// 初始化顺序表 void InitList(SeqList *L) {// 分配内存:InitSize 个 int 大小的空间L->data = (int *)malloc(InitSize * sizeof(int));if (L->data == NULL) { // 检查内存分配是否失败printf("内存分配失败!\n");exit(1); // 直接终止程序(也可返回错误码处理)}L->length = 0; // 初始化为空表L->MaxSize = InitSize; // 设置初始最大容量 }// 扩容函数:将最大容量增加 len void IncreaseSize(SeqList *L, int len) {int *p = L->data; // 保存原数据的地址(用于释放和拷贝)// 分配新内存:原容量 + lenL->data = (int *)malloc((L->MaxSize + len) * sizeof(int));if (L->data == NULL) {printf("内存扩容失败!\n");exit(1);}// 拷贝原有数据到新内存for (int i = 0; i < L->length; i++) {L->data[i] = p[i];}L->MaxSize += len; // 更新最大容量free(p); // 释放原内存(避免内存泄漏) }int main() {SeqList L; // 声明顺序表变量InitList(&L); // 初始化(传地址,因为函数参数是指针)// 【示例】手动插入几个元素(演示用,实际可封装插入函数)for (int i = 0; i < 5; i++) {if (L.length < L.MaxSize) { // 确保不超出容量L.data[L.length++] = i; // 插入数据并更新长度}}printf("扩容前:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 扩容:最大容量增加 5IncreaseSize(&L, 5);printf("扩容后:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 释放动态分配的内存(必须!否则内存泄漏)free(L.data);return 0; }程序运行结果如下:
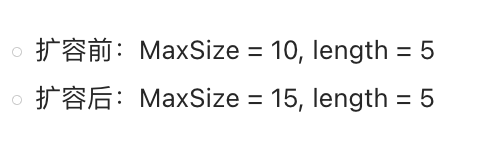
- 定义动态顺序表
-
使用标准库专门用于 “调整已分配内存大小” 的函数
realloc- 顺序表结构体和初始化方法不变,扩容的方法为:
// 扩容:容量翻倍(用 realloc) void Expand(SeqList *L) {int *new_data = realloc(L->data, 2 * L->MaxSize * sizeof(int));if (new_data == NULL) {printf("扩容失败!\n");return;}L->data = new_data; // 更新指针L->MaxSize *= 2; // 容量翻倍printf("扩容成功!新容量:%d\n", L->MaxSize); } - main 函数中执行方法
int main() {SeqList L; // 声明顺序表变量InitList(&L); // 初始化(传地址,因为函数参数是指针)// 手动插入几个元素(演示用,实际可封装插入函数)for (int i = 0; i < 5; i++) {if (L.length >= L.MaxSize) { // 确保不超出容量Expand(L);}L.data[L.length++] = i;}printf("扩容前:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 扩容:最大容量增加 5IncreaseSize(&L, 5);printf("扩容后:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 释放动态分配的内存(必须!否则内存泄漏)free(L.data);return 0; }
完整代码如下:
#include <stdio.h> #include <stdlib.h>typedef struct {int *data; // 动态数组int MaxSize; // 当前最大容量int length; // 实际长度 } SeqList;// 初始化:初始容量为10 void InitList(SeqList *L) {L->data = (int*)malloc(10 * sizeof(int));L->MaxSize = 10;L->length = 0; }// 扩容:容量翻倍(用 realloc) void Expand(SeqList *L) {int *new_data = realloc(L->data, 2 * L->MaxSize * sizeof(int));if (new_data == NULL) {printf("扩容失败!\n");return;}L->data = new_data; // 更新指针L->MaxSize *= 2; // 容量翻倍printf("扩容成功!新容量:%d\n", L->MaxSize); }int main() {SeqList L; // 声明顺序表变量InitList(&L); // 初始化(传地址,因为函数参数是指针)printf("扩容前:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 手动插入几个元素(演示用,实际可封装插入函数)for (int i = 0; i < 15; i++) {if (L.length >= L.MaxSize) { // 确保不超出容量Expand(&L);}L.data[L.length++] = i;}printf("扩容后:MaxSize = %d, length = %d\n", L.MaxSize, L.length);// 释放动态分配的内存(必须!否则内存泄漏)free(L.data);return 0; }程序运行结果如下:

- 顺序表结构体和初始化方法不变,扩容的方法为:
顺序表的特性:
- 具有随机访问特性,可在常数级时间找到元素;
- 存储密度高,仅存储数据元素本身;
- 静态分配不可拓展容量,动态分配拓展容量时间开销高;
- 插入删除操作不方便,需移动大量元素。
顺序表的插入
插入操作的基本概念:插入操作是往线性表的第 i 个位置(位序,从 1 开始)插入指定元素 e。以静态分配的顺序表为例,若要在第三个位置插入元素,需将第三个位置及之后的元素依次后移,再插入新元素,同时顺序表长度加 1。
// 插入元素:在位置i插入元素e (1-based)
int Insert(SeqList *L, int i, int e) {if (i < 1 || i > L->length + 1) return 0; // 插入位置非法if (L->length >= MAXSIZE) return 0; // 表已满for (int j = L->length; j >= i; j--) {L->data[j] = L->data[j-1];}L->data[i-1] = e;L->length++;return 1;
}
这段代码是顺序表的插入操作实现,功能是在顺序表的指定位置(1-based,即从 1 开始计数)插入一个新元素,下面逐行解释其逻辑:
- 函数定义
int Insert(SeqList *L, int i, int e)- 作用:向顺序表中插入元素
- 参数:
SeqList *L:指向顺序表的指针(需要修改原顺序表,所以传指针)int i:插入位置(1-based,例如 i=1 表示插入到第一个位置)int e:要插入的元素值
- 返回值:
1表示插入成功,0表示插入失败
- 插入位置合法性检查
if (i < 1 || i > L->length + 1) return 0;- 顺序表的插入位置有严格限制:
- 最小位置是
1(不能在第 0 个位置之前插入); - 最大位置是
L->length + 1(可以插入到当前表的末尾,即最后一个元素的后面)。
- 最小位置是
- 例如:如果当前表长度为 3(有 3 个元素),合法的插入位置是
1、2、3、4(分别对应 “第 1 个元素前” 到 “第 3 个元素后”)。 - 若
i不在这个范围,返回0(插入失败)。
- 顺序表的插入位置有严格限制:
- 表满检查
if (L->length >= MAXSIZE) return 0;- 顺序表的最大容量由
MAXSIZE定义(静态顺序表的固定大小)。 - 若当前表的长度(
L->length)已经等于或超过MAXSIZE,说明表已满,无法插入新元素,返回0(插入失败)。
- 顺序表的最大容量由
- 元素后移(核心步骤)
for (int j = L->length; j >= i; j--) {L->data[j] = L->data[j-1]; }- 插入元素前,需要将插入位置及之后的元素向后移动一位,腾出插入位置。
- 为什么从后往前移?
假设从前往后移(j从i开始),会导致后面的元素被前面的元素覆盖(例如:data[i]会先被data[i-1]覆盖,导致data[i]的原值丢失)。 - 示例:
原表:[10, 20, 30](长度 3,MAXSIZE=5),要在 i=2(第 2 个位置)插入 25。- 循环从 j=3(当前长度)开始,到 j=2(插入位置 i=2)结束:
j=3:data[3] = data[2]→ 表变为[10, 20, 30, 30]j=2:data[2] = data[1]→ 表变为[10, 20, 20, 30]
- 移动后,
i=2对应的索引1(因为数组是 0-based)位置被腾出。
- 循环从 j=3(当前长度)开始,到 j=2(插入位置 i=2)结束:
- 插入新元素
L->data[i-1] = e;- 顺序表的存储数组
data是 0-based(从 0 开始计数),而插入位置i是 1-based,因此需要转换为索引i-1。 - 示例:上述例子中
i=2,对应索引1,执行data[1] = 25→ 表变为[10, 25, 20, 30]。
- 顺序表的存储数组
- 更新表长度
L->length++; return 1;- 插入成功后,表的实际长度加 1(
length是当前元素个数)。 - 返回
1表示插入成功。
- 插入成功后,表的实际长度加 1(
完整的实现如下所示:
#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 10typedef struct {int data[MAXSIZE]; // 存放元素的数组int length; // 当前表的长度
} SeqList;// 初始化顺序表
void InitList(SeqList *L) {L->length = 0;
}// 插入元素:在位置i插入元素e (1-based)
int Insert(SeqList *L, int i, int e) {if (i < 1 || i > L->length + 1) return 0; // 插入位置非法if (L->length >= MAXSIZE) return 0; // 表已满for (int j = L->length; j >= i; j--) {L->data[j] = L->data[j-1];}L->data[i-1] = e;L->length++;return 1;
}int main() {SeqList L;InitList(&L);Insert(&L, 1, 10);Insert(&L, 2, 20);Insert(&L, 3, 30);printf("顺序表元素: ");for (int i = 0; i < L.length; i++) {printf("%d ", L.data[i]);}printf("\n");return 0;
}
程序运行结果如下:

插入操作的时间复杂度:
-
最好情况:新元素插入到表尾,不需要移动元素 i=n+1i = n+1i=n+1,循环 0 次;最好时间复杂度 = O(1)O(1)O(1)
-
最坏情况:新元素插入到表头,需要将原有的 n 个元素全都向后移动 i=1i = 1i=1,循环 n 次;最坏时间复杂度 = O(n)O(n)O(n)
-
平均情况:
假设新元素插入到任何一个位置的概率相同,即 i=1,2,3,…,length+1i = 1,2,3, \dots, \text{length+1}i=1,2,3,…,length+1 的概率都是 p=1n+1p = \boldsymbol{\dfrac{1}{n+1}}p=n+11
- i=1i = 1i=1,循环 nnn 次;
- i=2i=2i=2 时,循环 n−1n-1n−1 次;
- i=3i=3i=3,循环 n−2n-2n−2 次 ……
- i=n+1i=n+1i=n+1 时,循环 0 次
平均循环次数 = np+(n−1)p+(n−2)p+⋯+1⋅p=n(n+1)2⋅1n+1=n2⇒np + (n-1)p + (n-2)p + \dots + 1 \cdot p= \frac{n(n+1)}{2} \cdot \frac{1}{n+1} = \frac{n}{2}\boldsymbol{\Rightarrow}np+(n−1)p+(n−2)p+⋯+1⋅p=2n(n+1)⋅n+11=2n⇒ 平均时间复杂度 = O(n)O(n)O(n)
顺序表的删除
删除操作的基本概念及代码实现:删除操作是删除线性表中第 i 个位置的元素,需将该元素后面的元素依次前移,同时顺序表长度减 1。代码中删除操作的参数 e 为引用型,用于返回被删除的元素,且顺序表参数也需加引用,确保操作影响原顺序表。
// 删除元素:删除位置i的元素
int Delete(SeqList *L, int i, int *e) {if (i < 1 || i > L->length) return 0;*e = L->data[i-1];for (int j = i; j < L->length; j++) {L->data[j-1] = L->data[j];}L->length--;return 1;
}
这段代码是顺序表的删除操作实现,功能是删除顺序表中指定位置(1-based,从 1 开始计数)的元素,并通过指针返回被删除的元素值。下面逐行解释其逻辑:
- 函数定义
int Delete(SeqList *L, int i, int *e)- 作用:删除顺序表中指定位置的元素,并返回被删除的元素
- 参数:
SeqList *L:指向顺序表的指针(需要修改原顺序表,因此传指针)int i:要删除的位置(1-based,例如 i=2 表示删除第 2 个元素)int *e:指针,用于存储被删除的元素值(通过指针 “传出” 结果)
- 返回值:
1表示删除成功,0表示删除失败
- 删除位置合法性检查
if (i < 1 || i > L->length) return 0;- 顺序表的删除位置必须是
已存在的元素位置:- 最小位置是
1(不能删除第 0 个位置,因为元素从 1 开始计数); - 最大位置是
L->length(不能删除超过当前表长的位置,例如表长为 3 时,只能删除 1、2、3 位置)。
- 最小位置是
- 若
i不在这个范围(位置非法),返回0(删除失败)。
- 顺序表的删除位置必须是
- 保存被删除的元素
*e = L->data[i-1];- 顺序表的存储数组
data是 0-based(从 0 开始计数),而删除位置i是 1-based,因此需要转换为索引i-1。 - 通过指针
e将被删除的元素值 “传出” 函数(例如,调用时传入&val,则val会被赋值为被删除的元素)。
- 顺序表的存储数组
- 元素前移(核心步骤)
for (int j = i; j < L->length; j++) {L->data[j-1] = L->data[j]; }- 删除元素后,需要将删除位置后面的所有元素向前移动一位,填补被删除元素的空位。
- 为什么从前往后移?
假设删除第 i 个元素(对应数组索引 i-1),后面的元素(i, i+1, …, length-1)需要依次前移:j从i(1-based)开始,对应数组索引j-1(删除位置的下一个元素);- 每次将
data[j](当前元素)赋值给data[j-1](前一个位置),直到移动完最后一个元素。
- 示例:
原表:[10, 25, 20, 30](长度 4),删除 i=2(第 2 个元素,值为 25)。- 循环从 j=2(1-based)开始,到 j<4(表长)结束:
j=2:data[1] = data[2]→ 表变为[10, 20, 20, 30]j=3:data[2] = data[3]→ 表变为[10, 20, 30, 30]
- 移动后,被删除元素的位置被后面的元素填补,最后一个元素(索引 3)变为冗余值(但不影响,因为后续会更新表长)。
- 循环从 j=2(1-based)开始,到 j<4(表长)结束:
- 更新表长度
L->length--; return 1;- 删除成功后,表的实际长度减 1(
length是当前元素个数,删除后减少一个)。 - 返回
1表示删除成功。
- 删除成功后,表的实际长度减 1(
完整的实现如下所示:
#include <stdio.h>
#include <stdlib.h>#define MAXSIZE 100typedef struct {int data[MAXSIZE]; // 存放元素的数组int length; // 当前表的长度
} SeqList;// 初始化顺序表
void InitList(SeqList *L) {L->length = 0;
}// 插入元素:在位置i插入元素e (1-based)
int Insert(SeqList *L, int i, int e) {if (i < 1 || i > L->length + 1) return 0; // 插入位置非法if (L->length >= MAXSIZE) return 0; // 表已满for (int j = L->length; j >= i; j--) {L->data[j] = L->data[j-1];}L->data[i-1] = e;L->length++;return 1;
}// 删除元素:删除位置i的元素
int Delete(SeqList *L, int i, int *e) {if (i < 1 || i > L->length) return 0;*e = L->data[i-1];for (int j = i; j < L->length; j++) {L->data[j-1] = L->data[j];}L->length--;return 1;
}int main() {SeqList L;InitList(&L);Insert(&L, 1, 10);Insert(&L, 2, 20);Insert(&L, 3, 30);printf("顺序表元素: ");for (int i = 0; i < L.length; i++) {printf("%d ", L.data[i]);}printf("\n");int e;Delete(&L, 2, &e);printf("删除的元素: %d\n", e);printf("删除后顺序表: ");for (int i = 0; i < L.length; i++) {printf("%d ", L.data[i]);}printf("\n");return 0;
}
程序运行结果如下:

删除操作的时间复杂度:
- 最好情况:删除最后一个元素 i=lengthi = lengthi=length,无需移动元素 → O(1)O(1)O(1)
- 最坏情况:删除第一个元素 i=1i = 1i=1,需要移动 length−1length-1length−1 个元素 → O(n)O(n)O(n)
- 平均情况:假设删除每个位置的概率相同,平均移动次数为 n−12→O(n)\frac{n-1}{2} → O(n)2n−1→O(n)
顺序表的查找
按位查找
- 静态分配
- 存储结构
静态顺序表用一个定长数组存放元素,例如:#define MAXSIZE 100 typedef struct {int data[MAXSIZE];int length; // 当前长度 } SqList; - 按位查找
所谓“按位查找”,就是找顺序表中第i个位置上的元素(注意是逻辑位序,不是数组下标)。
因为:- 数组下标从 0 开始
- 顺序表位序从 1 开始
所以数组下标 =i - 1。
- 实现示例:
int GetElem(SqList L, int i) {if (i < 1 || i > L.length) { // 判断 i 合法性printf("位置不合法\n");return -1;}return L.data[i-1]; // 返回第 i 个元素 } - 特点
- 随机存取:直接通过下标算出地址 → O(1) 时间。
- 静态数组内存编译时已经确定。
- 存储结构
- 动态分配
- 存储结构
动态分配时,元素存储空间不是固定的,而是运行时用malloc申请:typedef struct {int *data; // 指针,指向一段连续存储空间int length; int maxSize; } SqList;void InitList(SqList *L, int maxSize) {L->data = (int*)malloc(maxSize * sizeof(int));L->length = 0;L->maxSize = maxSize; } - 按位查找
即使data是指针,也能像数组一样下标访问,因为 C 语言规定:data[i]实际上是*(data + i)。
int GetElem(SqList L, int i) {if (i < 1 || i > L.length) return -1;return L.data[i-1]; } - 特点
- 运行时决定表的容量,更灵活。
- 底层同样是连续内存,所以查找操作也是 O(1)。
- 存储结构
- 时间复杂度分析
- 按位查找不需要循环和递归。
- 只做 一次地址计算 + 一次访问 → O(1)。
- 这就是“顺序表的随机存取特性”:内存连续,元素大小相同,所以可以通过公式:
直接定位。地址 = 基地址 + (i-1) * 元素大小
按值查找
- 基本思路
- 从头到尾依次扫描表元素,找到与给定值
e相等的元素。 - 若找到 → 返回其位序(数组下标 + 1)。
- 若没找到 → 返回 0 或 -1 表示失败。
- 从头到尾依次扫描表元素,找到与给定值
- 基本数据类型(int、char)
- 直接用
==比较。 - 示例代码:
int LocateElem(SqList L, int e) {for (int i = 0; i < L.length; i++) {if (L.data[i] == e) {return i + 1; // 位序}}return 0; // 没找到 }
- 直接用
- 结构体类型
- 如果表中元素是结构体,不能直接
==比较。 - C语言中需要逐一比较成员:
typedef struct {int id;char name[20]; } Student;bool equal(Student a, Student b) {return (a.id == b.id && strcmp(a.name, b.name) == 0); }
- 如果表中元素是结构体,不能直接
- 时间复杂度分析
- 最好情况:目标元素就在第一个位置 → 只比较一次 → O(1)O(1)O(1)。
- 最坏情况:目标元素在最后,或者不存在 → 比较 nnn 次 → O(n)O(n)O(n)。
- 平均情况:假设目标元素等概率分布在各位置,平均比较次数为:
1+2+⋯+nn=n+12{1+2+⋯+n \over n}={n+1 \over 2}n1+2+⋯+n=2n+1
所以平均时间复杂度 = O(n)O(n)O(n)。
代码实现
- 静态分配
程序运行结果如下:#include <stdio.h> #include <stdlib.h>#define MAXSIZE 100 typedef struct {int data[MAXSIZE]; // 静态数组int length; // 当前长度 } SqList_Static;// 按位查找(静态) int GetElem_Static(SqList_Static L, int i) {if (i < 1 || i > L.length) {printf("位置不合法\n");return -1;}return L.data[i - 1]; }// 按值查找(静态) int LocateElem_Static(SqList_Static L, int e) {for (int i = 0; i < L.length; i++) {if (L.data[i] == e) return i + 1; // 返回位序}return 0; // 未找到 }int main() {SqList_Static sList;sList.length = 5;for (int i = 0; i < sList.length; i++) {sList.data[i] = (i + 1) * 10; // [10, 20, 30, 40, 50]}printf("静态顺序表测试:\n");printf("第3个元素是:%d\n", GetElem_Static(sList, 3));printf("元素40的位置是:%d\n", LocateElem_Static(sList, 40));printf("元素99的位置是:%d\n\n", LocateElem_Static(sList, 99));return 0; }

- 动态分配
程序运行结果如下:#include <stdio.h> #include <stdlib.h>typedef struct {int *data; // 动态数组int length; // 当前长度int maxSize; // 最大容量 } SqList_Dynamic;// 初始化动态顺序表 void InitList(SqList_Dynamic *L, int maxSize) {L->data = (int*)malloc(maxSize * sizeof(int));L->length = 0;L->maxSize = maxSize; }// 按位查找(动态) int GetElem_Dynamic(SqList_Dynamic L, int i) {if (i < 1 || i > L.length) {printf("位置不合法\n");return -1;}return L.data[i - 1]; }// 按值查找(动态) int LocateElem_Dynamic(SqList_Dynamic L, int e) {for (int i = 0; i < L.length; i++) {if (L.data[i] == e) return i + 1;}return 0; }int main() {SqList_Dynamic dList;InitList(&dList, 10);dList.length = 5;for (int i = 0; i < dList.length; i++) {dList.data[i] = (i + 1) * 100; // [100, 200, 300, 400, 500]}printf("动态顺序表测试:\n");printf("第4个元素是:%d\n", GetElem_Dynamic(dList, 4));printf("元素300的位置是:%d\n", LocateElem_Dynamic(dList, 300));printf("元素999的位置是:%d\n", LocateElem_Dynamic(dList, 999));// 释放动态分配的内存free(dList.data);return 0; }

总结