梅森公式计算传递函数及结构图转换为信号流图过程

前言

梅森增益公式是在自动控制原理里面很重要的计算传递函数的公式，简单易操作，一定要掌握。本文通过公式和几个例题，讲解一下，希望大家理解。另外也附上了结构图转化为信号流图的方法，其实信号流图转换成结构图也类似的逻辑。

一、梅森公式

传递函数公式：

• 特征式，就是处于分母的部分，里面的符号负正交替，分别是单独回路的增益，两两不接触的回路增益乘积，三三互不接触的回路增益乘积……
• p_k就是从开头到结尾的通路上，这一路上遇到几个G(s)，全部乘积起来。
• 流图余子式，就是在框图上，在特征式当中，与此前向通路没有接触的部分，或者说，排除掉所有与此前向通路接触的部分。
• n，就是有几个前向通路，就是几。

例题一

1.1 单独回路增益

在结构框图里找单独的回路，并计算增益：

分别计算回路增益：

• L1 = -G2G3H2
• L2 = -G3G4H4
• L3 = -G4G5H3
• L4 = -G1G2G3G4G5G6H1

要注意负号！

1.2 两两不接触回路

只有L1和L3满足条件，

• L1L3 = G2G3H2G4G5H3

1.3 三个互不接触回路

无

1.4 特征式

• 等于：1 + G2G3H2 + G3G4H4 + G4G5H3 + G1G2G3G4G5G6H1 + G2G3H2G4G5H3

1.5 前向通路（从源节点到阱节点的所有通路）

只有一条前向通路增益，就是将前向通路所有的增益乘积。

• p₁ = G1G2G3G4G5G6

流图余子式，就是在框图上，在特征式当中，与此前向通路没有接触的部分，或者说，排除掉所有与此前向通路接触的部分，结果除了1以外，都有接触。

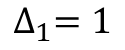
所以，传递函数：

例题二

绘制流程图太费时间了，所以就在纸上画出来，写出来计算过程，大家多多担待哈。

例题三（从信号流图计算传递函数）

3.1 题目

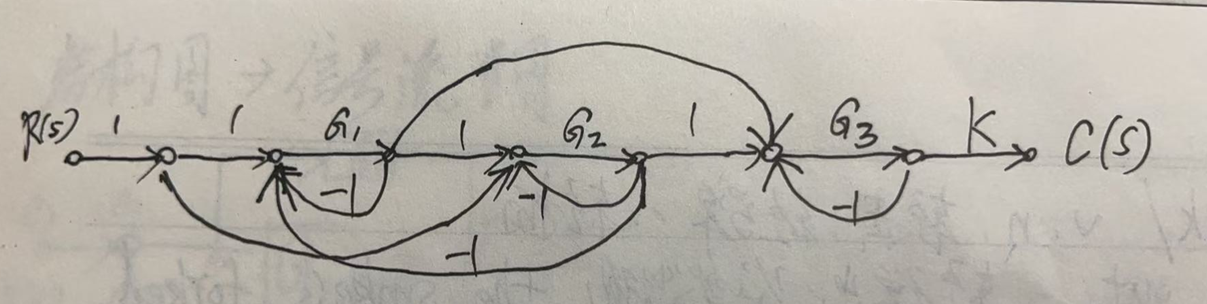
3.2 解题

这里将几条前向通路画出来，因为尤其第4条特别不容易找。第一条就是直着向右，不用画了，下面是第2条的前向通路。

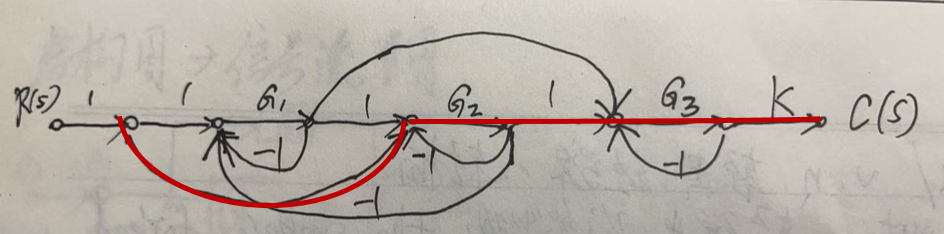
下面是第3条的前向通路。

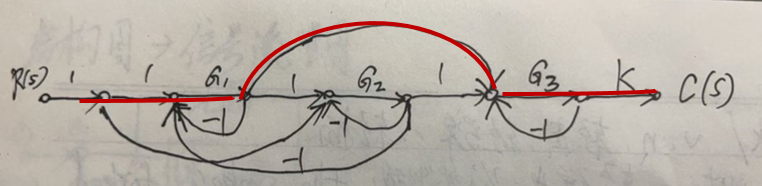
下面是第4条前向通路，其中有交叉的特意用不同颜色标出，其方向是从左到右。

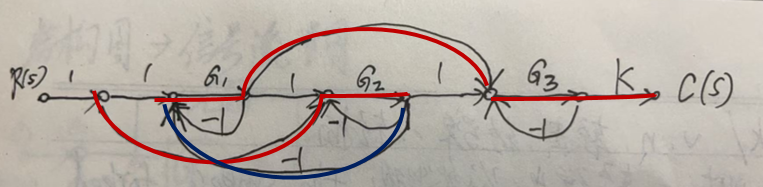
二、通过结构框图画信号流图

注意：

• 上图，信号流图的节点中，比较点是比较之后的结果再进行下一步的增益计算。
• 下面的部分是对信号流图的简化，不简化其实也是正确答案。

---

本文到此结束，关于自动控制原理的知识我还会继续分享，欢迎大家关注。