决策树（2）

 决策树算法

1. ID3

     核心是信息增益，即某个属性带来的熵增，信息增益越大，用该属性划分获得的“纯度提升”越大，故以此选择划分属性。

     存在缺陷，其信息增益准则对可取值数目较多的属性有所偏好，例如可能会将“编号”作为最优划分。

2. C4.5

     采用信息增益率来选择划分属性，信息增益率的计算方式为信息增益除以该属性自身的熵。

3. CART

     以基尼指数作为划分依据，基尼指数\(Gini(D)\)反映了从数据集\(D\)中随机抽取两个样本，其类别标记不一致的概率。

     其中\(p\)（某类别概率）越大，\(Gini(D)\)越小，数据集\(D\)的纯度越高。

 连续值处理

 对于连续值，可采用贪婪算法选取分界点，具体步骤为：先对连续值进行排序，然后考虑可能的二分分界点，这一过程实际上是“离散化”过程。例如，对于一系列Taxable Income值，可分割成\(TaxIn<=80\)和\(TaxIn>80\)，或\(TaxIn<=97.5\)和\(TaxIn>97.5\)等。

 决策树剪枝策略

剪枝原因：决策树过拟合风险很大，理论上可完全分开数据，故需剪枝。

预剪枝：边建立决策树边进行剪枝，更实用。可通过限制深度、叶子节点个数、叶子节点样本数、信息增益量等方式实现。

后剪枝：建立完决策树后进行剪枝。衡量标准为最终损失=自身的GINI系数值+α×叶子节点数量。α越大，越不易过拟合，但结果可能欠佳；α越小，更注重结果好坏，过拟合可能较严重。同时，会根据验证集精度决定是否剪枝，如某分支剪枝后精度提升则进行剪枝。

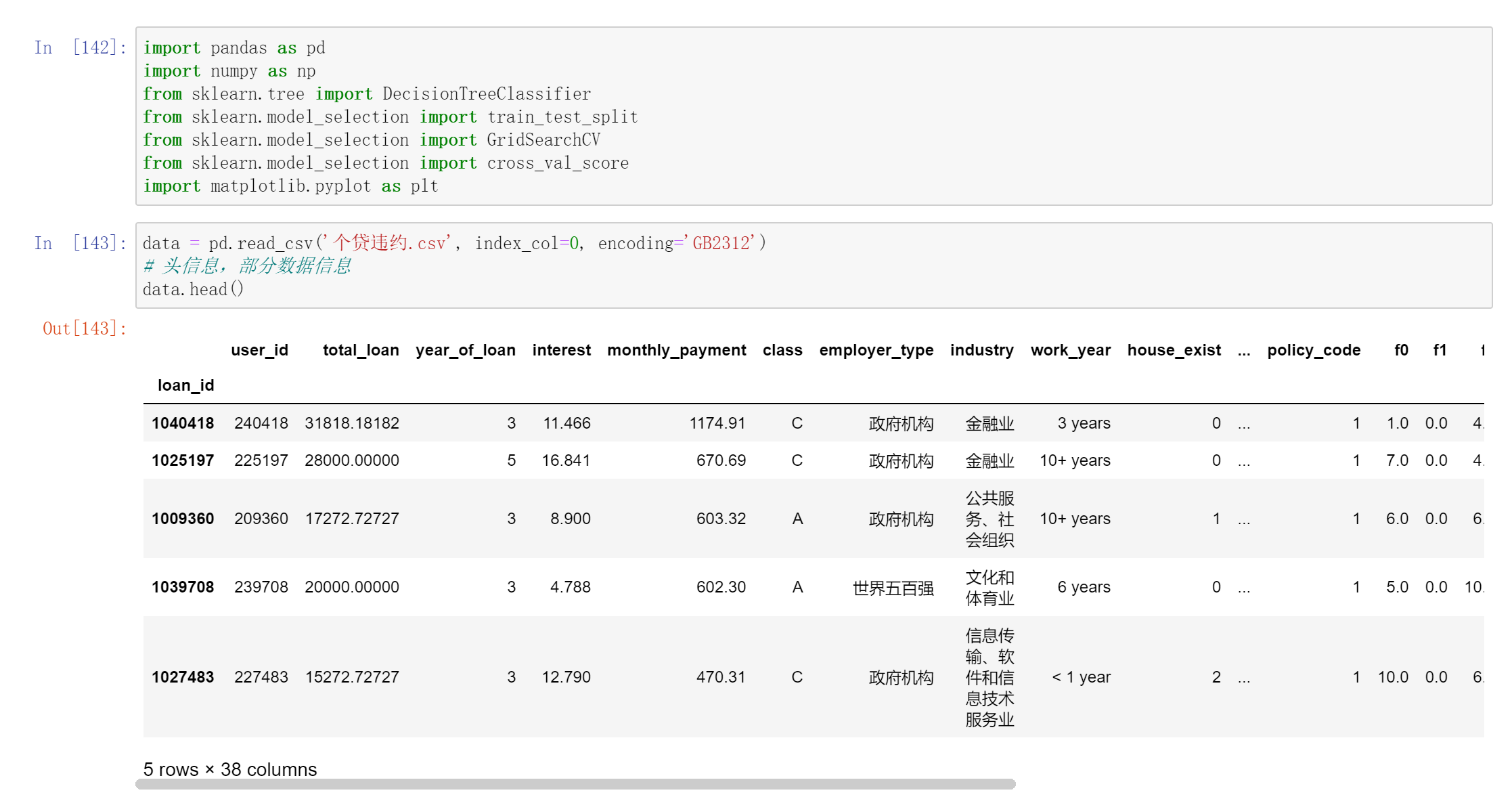
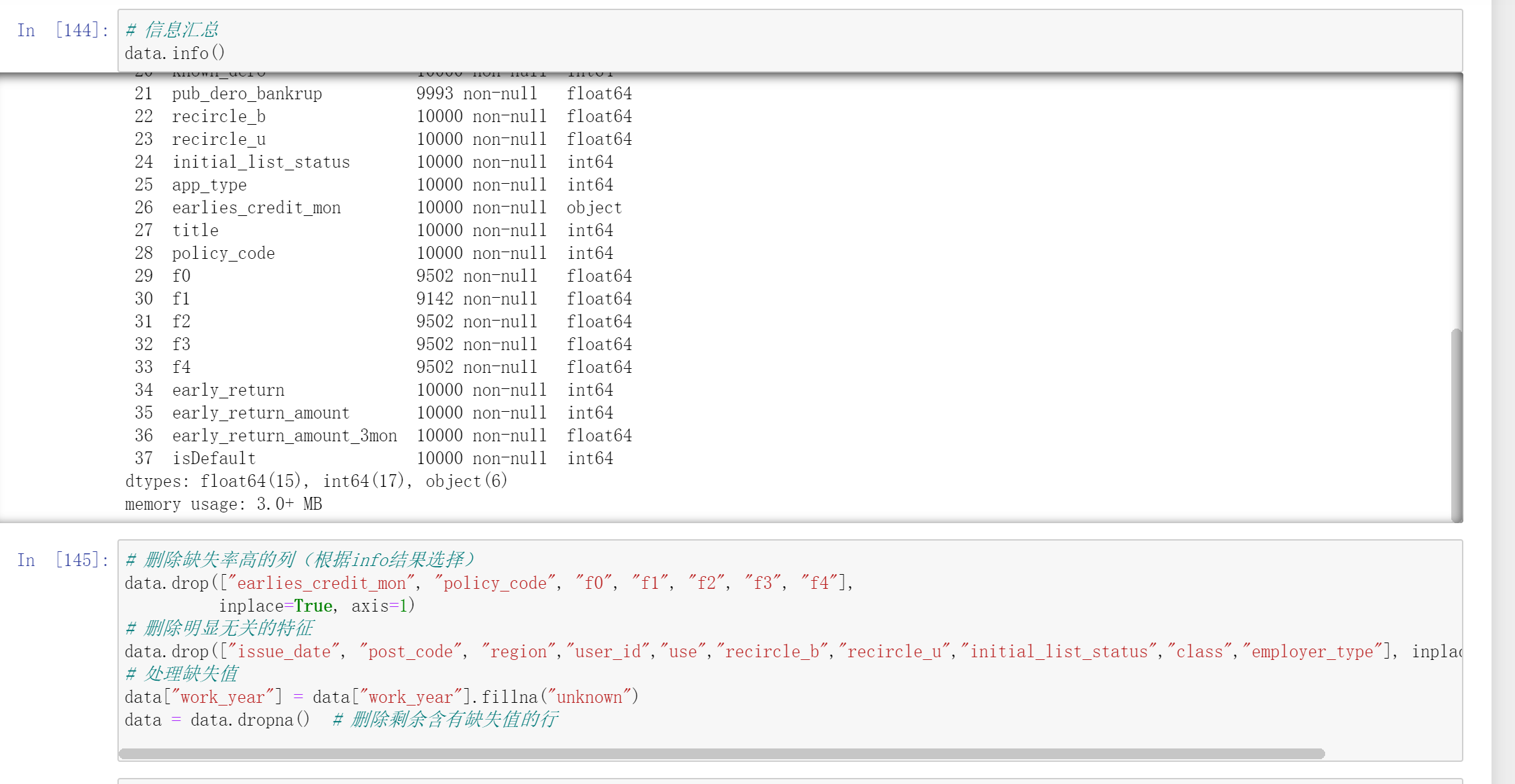
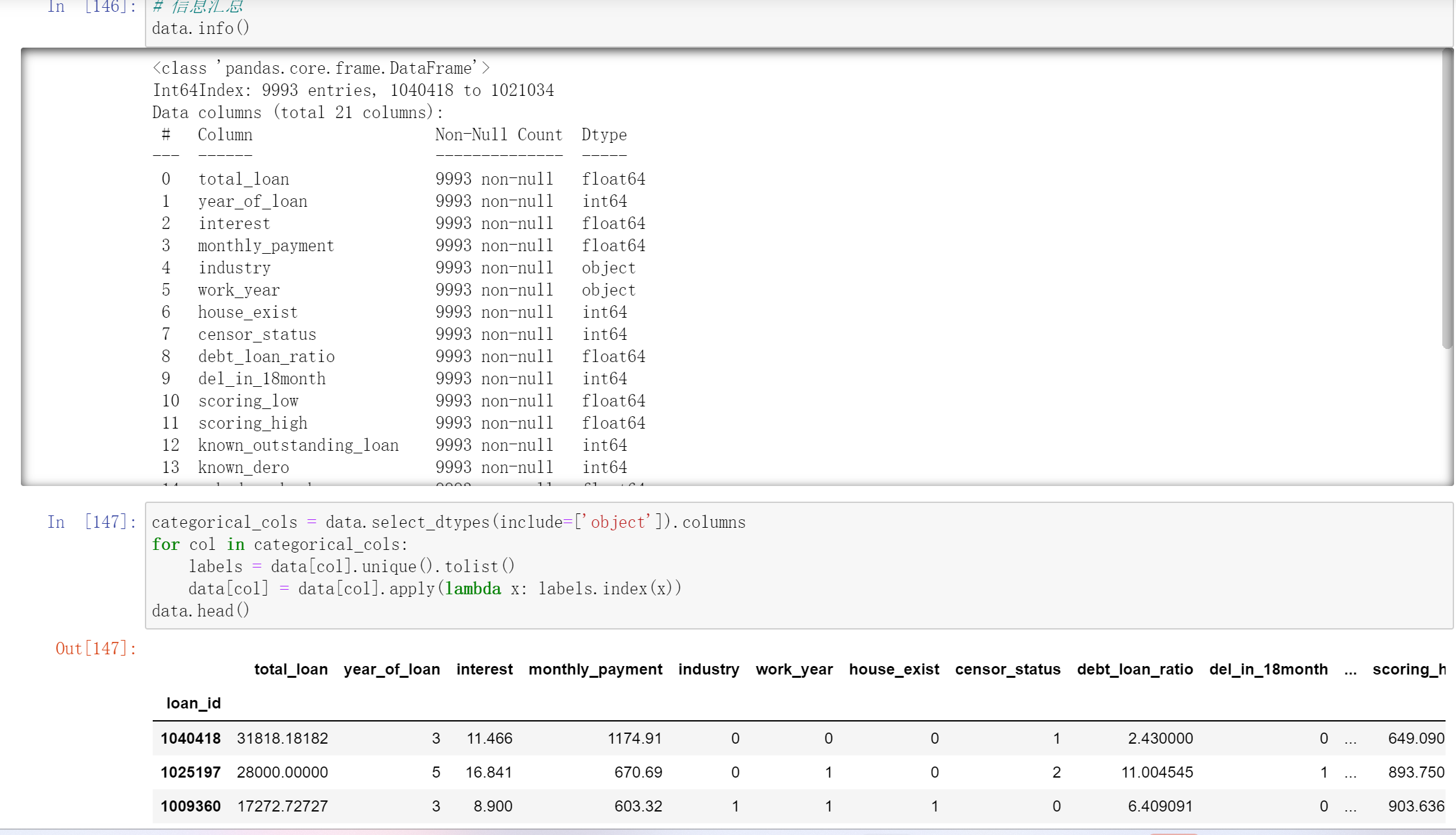
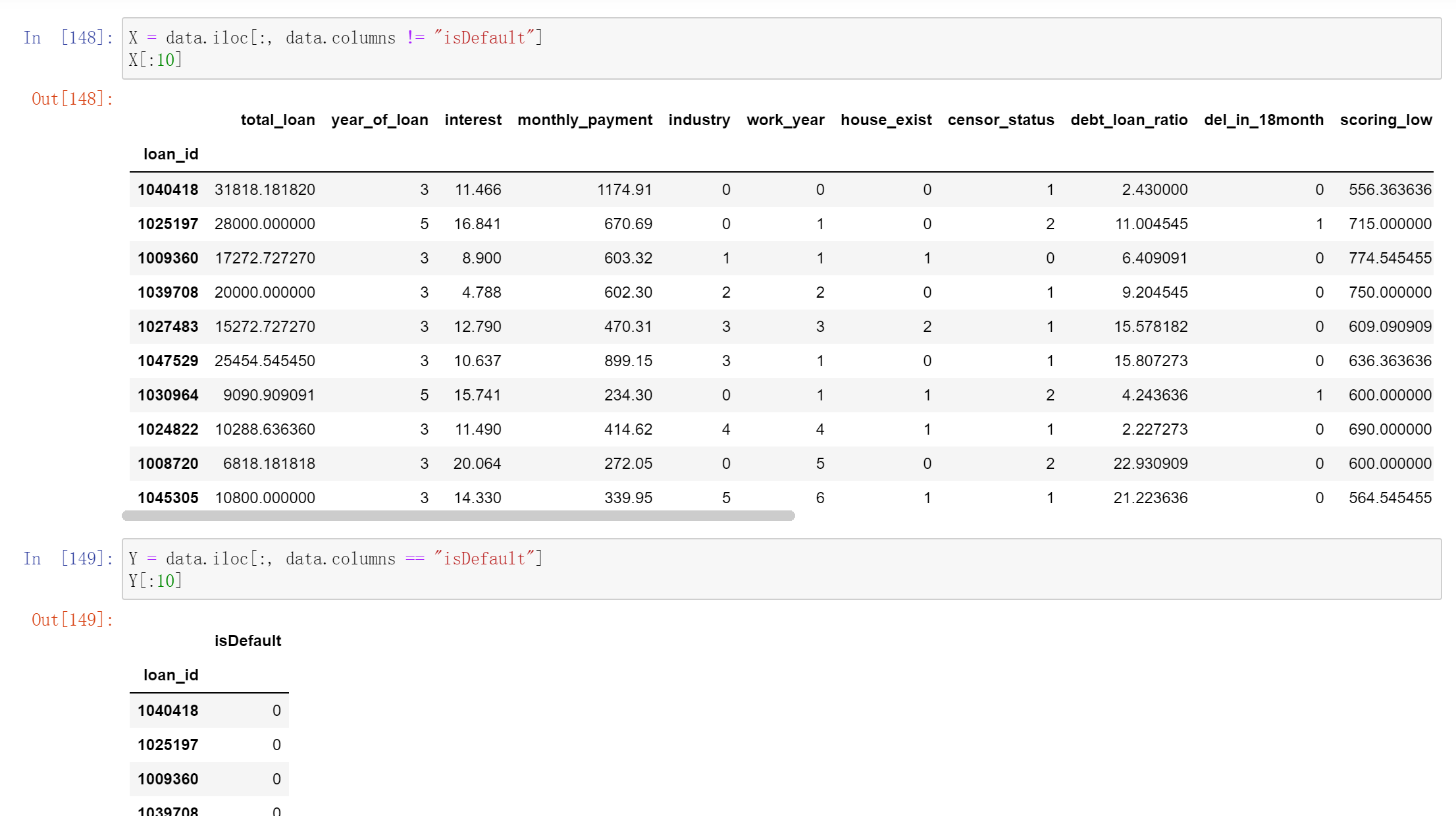
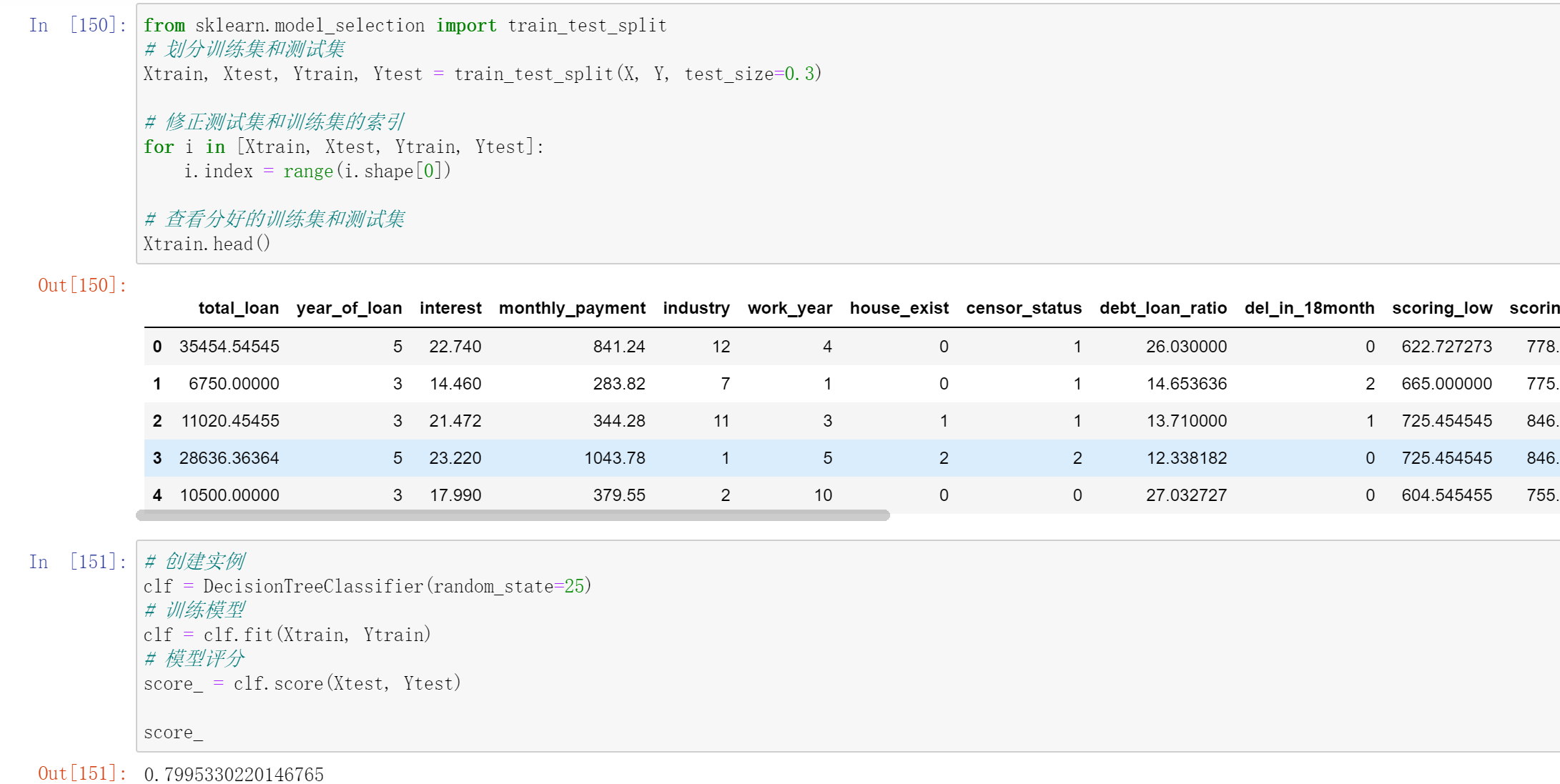
 决策树代码实现

 可通过`DecisionTreeClassifier()`创建决策树模型，其主要参数包括：

    criterion`：可选gini（基尼系数）或者entropy（信息熵）。

    splitter：可选best（在所有特征中找最好的切分点）或者random（在部分特征中找切分点）。

    max_features：可选None（所有）、log2、sqrt、N。

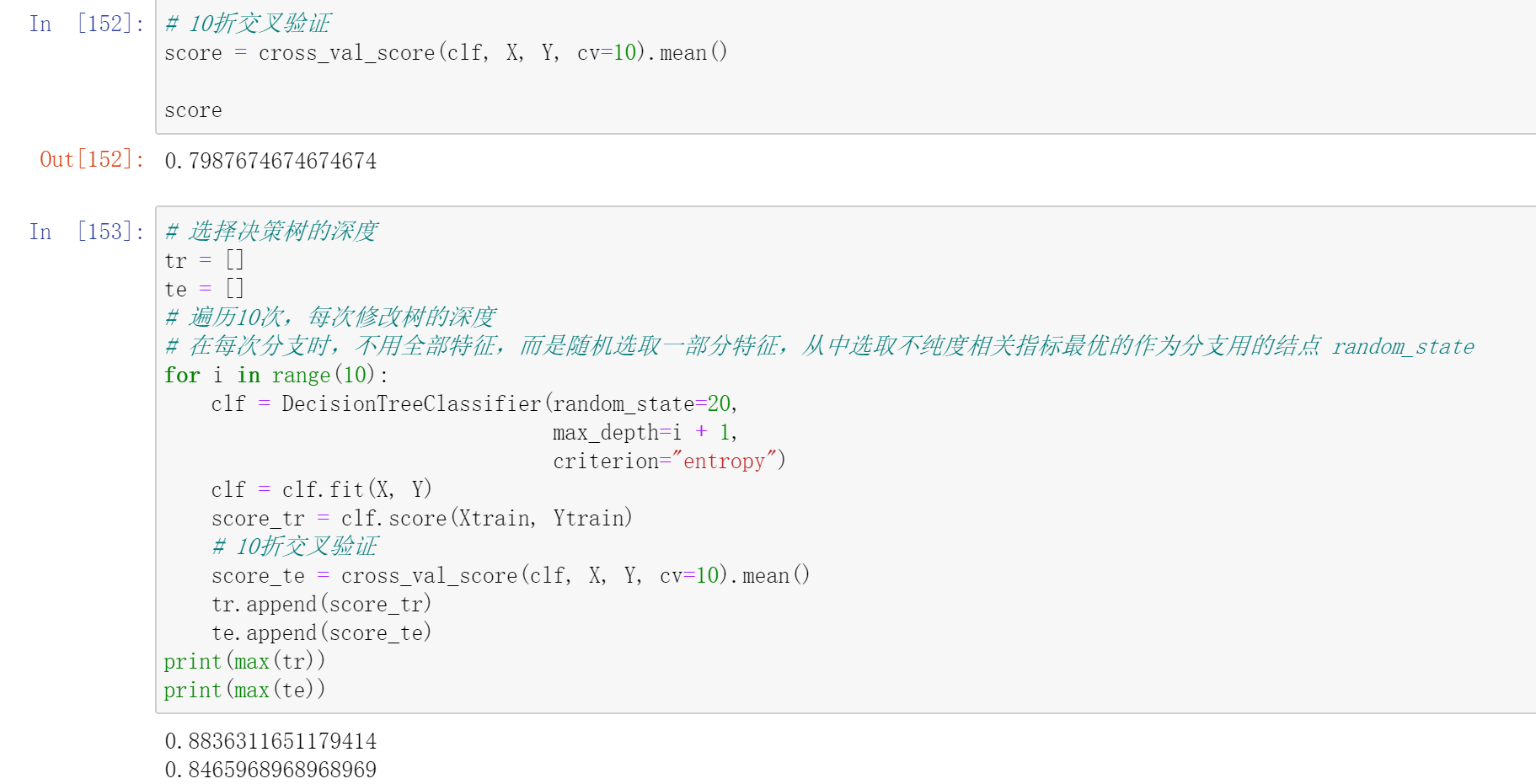
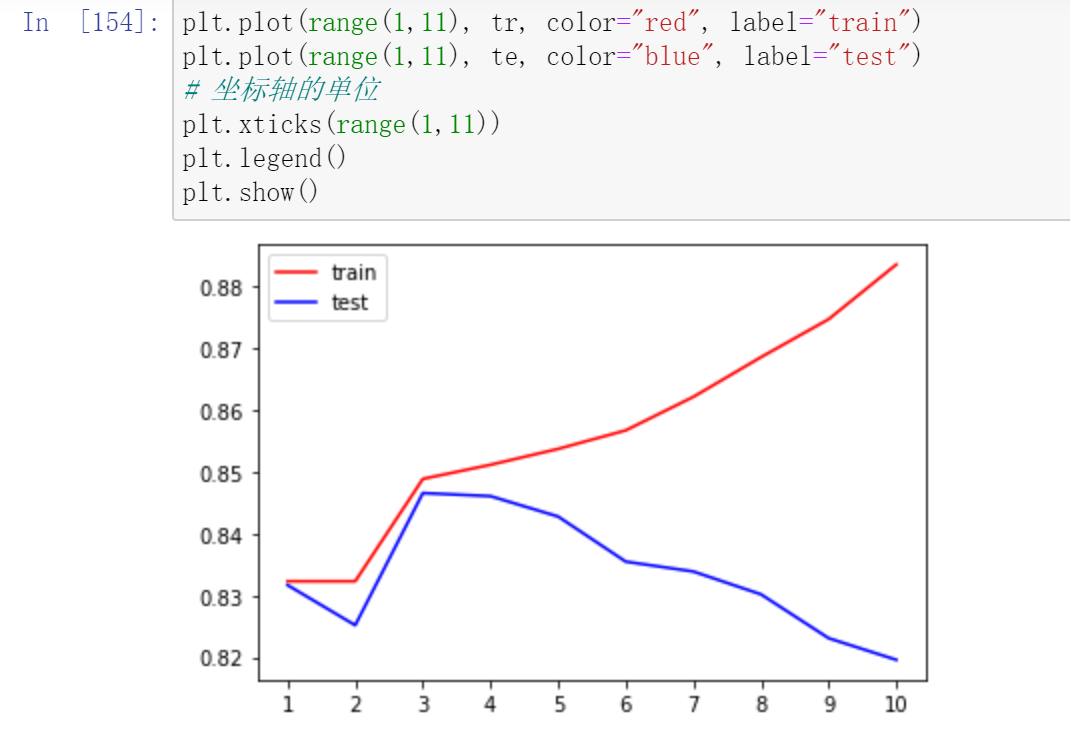
    max_depth：可选int或None，默认None，用于设置决策树的最大深度，深度越大越易过拟合，推荐深度在5-20之间。

预测泰坦尼克号