强化学习-CH3 最优状态值和贝尔曼最优方程

强化学习-CH3 最优状态值和贝尔曼最优方程

3.1 最优状态值（state values）和最优策略(policies)

定义：（根据状态值去定义）对于每一个状态都有最大的状态值

3.2 贝尔曼最优方程（BOE）

对于每一个状态s，它的贝尔曼最优方程的表达形式为：（π（s）表示状态s的一个策略）

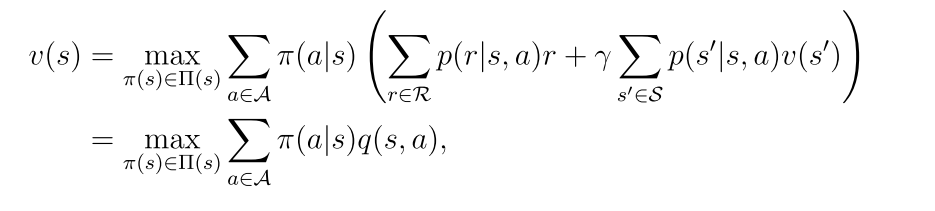
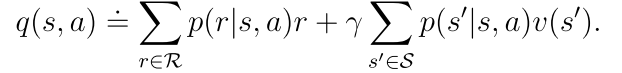
3.2.1 最大化BOE的右边

如何求解：（有两个未知值，一个是v(s)，一个是π（a|s））

因为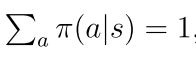

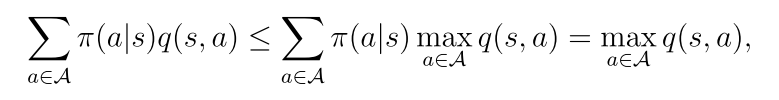
当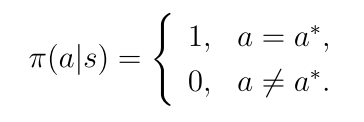

其中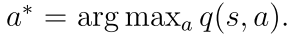

最优策略π(s)是选择q（s, a）值最大的策略。

3.2.2 BOE的向量形式

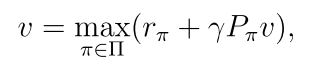
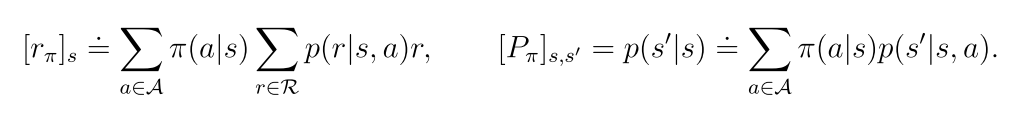
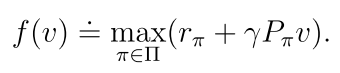
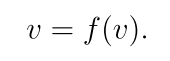
3.2.3 不动点定理

不动点：x1 = f(x1) x1既是不动点

收缩映射（contraction mapping）：存在γ∈（0,1），使得

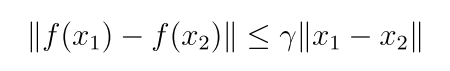
定理（收缩映射）：对任意等式x=f(x)，其中x和f(x)都是实向量，如果f是一个收缩映射，那么以下结论成立：

（1）一定存在一个不动点

（2）不动点是唯一的

（3）迭代算法

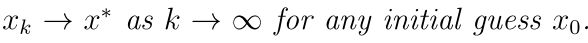
由此可以看到，BOE也符合收缩映射定理

3.3 从BOE中求解最优策略

（1）求解v*

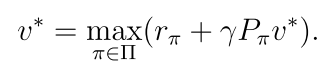
迭代法：

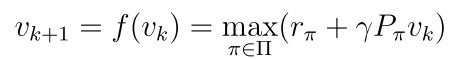
（2）求解π*

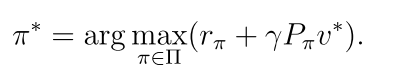
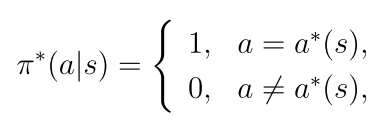
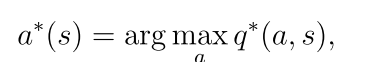
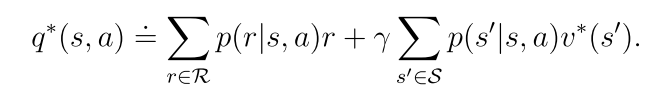
对于最优状态值它是唯一的，而对于最优策略不是唯一的，且一定存在一个确定性的最优策略（可能存在不确定的最优策略）

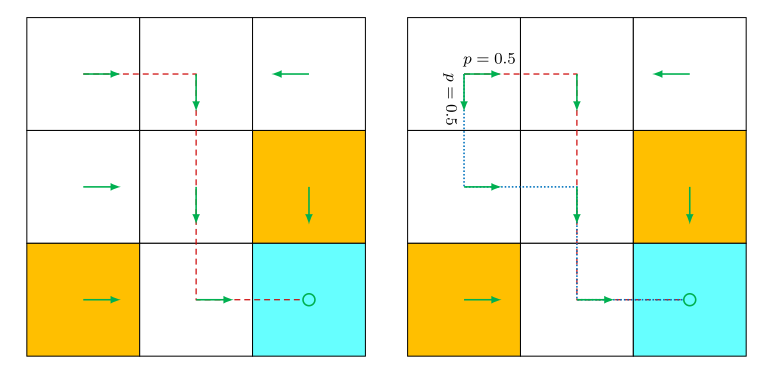
总结：对于贝尔曼方程，列出了状态值之间的关系，可以通过迭代法进行求解，从状态值又引出了动作值

对于BOE，它是一种特殊的贝尔曼方程，在原先的基础上求解最优的状态值和策略。根据收缩映射定理，也是通过迭代法求解最优状态值，进而获取动作值，由贪心算法，对于每个状态的策略选取动作值最大的动作，执行概率为1.

3.4 影响最优策略的因素

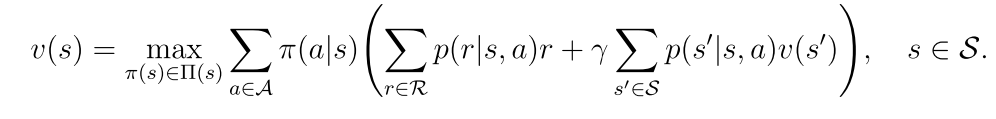
（1）折扣率：γ的大小决定重视立即奖励还是未来奖励

（2）奖励：决定机器人是否进入到惩罚区域

[外链图片转存中…(img-95Ln67Ew-1755593443296)]

（1）折扣率：γ的大小决定重视立即奖励还是未来奖励

（2）奖励：决定机器人是否进入到惩罚区域

如果扩大所有奖励或给所有奖励增加相同的值，最优策略保持不变。