二分法专题训练
首先是灵神的模板讲解:
[5,7,7,8,8,10],返回有序数组中第一个大于等于8的位置
闭区间写法:
如果是令le=0;ri=len-1的话,这里就是闭区间的写法!
mid=(le+ri)/2 注意到这里le+ri可能会有溢出的问题(注意细节),所以正确的写法应该是下减后加(养成习惯!)
对于闭区间写法,如果num[mid]<8,那么le=mid+1;换而言之0-mid被排除,所以更新le
这里le不更新为mid,原因是闭区间!如果是mid,ri就是左开右闭了 同理更新ri=mid-1
注意到:看上面的更新过程,所以到最后:

左闭右开的半闭区间写法:
把ri改为len while中循环条件区间不为空改为le<ri ,当mid>=target的时候,答案在左边;
ri不再是mid-1,而是mid(开区间写法)
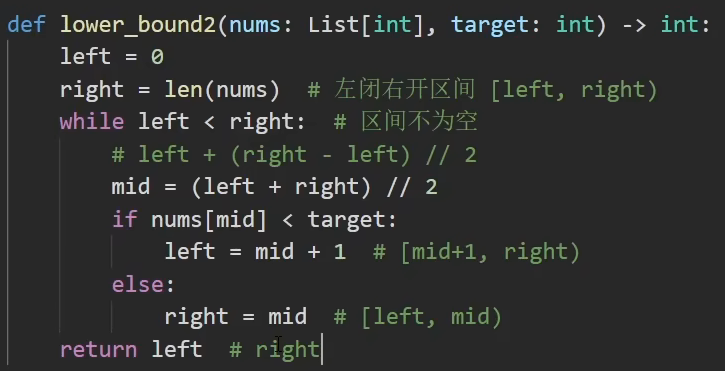
疑惑:和下面一样,我要求第一个大于等于8的位置,当nums[mid]>=target时(也就是else),mid应该包含在答案里面,为啥这里是开区间呢?
答:看最后的返回值是left 都是返回的if为不满足的
开区间写法:
le初始化为-1,ri初始化为len,while不为空条件:le+1<ri (开区间!)

最后ri是指向答案的(关于指向答案,其实也可以通过这个例子画图来看!)
所以推荐开区间写法,不需要考虑加1
上面的例子是针对大于等于的,对于大于的题,转换成>=x+1;小于和小于等于同理
闭区间的cpp模板:
闭区间两个都要加减1;此外,对加一减一,不要从答案是否包含的角度去想,要从尝试的角度去理解:比如尝试在左半部分找更小的位置
int lower_bound_closed(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1; int result = nums.size();while (left <= right) {int mid = left + (right - left) / 2; // 防止溢出if (nums[mid] >= target) {result = mid; right = mid - 1; // 尝试在左半部分找更小的位置} else {left = mid + 1; // 当前mid不满足,向右移动}}return result;
}744.寻找比目前字母大的最小字母
给你一个字符数组 letters,该数组按非递减顺序排序,以及一个字符 target。letters 里至少有两个不同的字符。
返回 letters 中大于 target 的最小的字符。如果不存在这样的字符,则返回 letters 的第一个字符。
开区间模板:
class Solution {
public:char nextGreatestLetter(vector<char>& letters, char target) {int le=-1;int ri=letters.size();while(le+1<ri){int mid=(ri-le)/2+le;if(letters[mid]<=target)le=mid;else if(letters[mid]>target)ri=mid;}if(le+1==letters.size())return letters[0];return letters[le+1];}
};2529.正整数和负整数的最大计数
给你一个按 非递减顺序 排列的数组 nums ,返回正整数数目和负整数数目中的最大值。
- 换句话讲,如果
nums中正整数的数目是pos,而负整数的数目是neg,返回pos和neg二者中的最大值。
注意:0 既不是正整数也不是负整数。
class Solution {
public:int maximumCount(vector<int>& nums) {//找到第一个大于0的位置int le=-1;int len=nums.size();int ri=len;while(le+1<ri){int mid=(ri-le)/2+le;if(nums[mid]<=0)le=mid;else ri=mid;}int a=le;int b=-1;while(a>=0){if(nums[a]==0)a--;else if(nums[a]<0){b=a;break;}}int ans=max(len-le-1,b+1);return ans;}
};1283.使结果不超过阈值的最小除数
给你一个整数数组 nums 和一个正整数 threshold ,你需要选择一个正整数作为除数,然后将数组里每个数都除以它,并对除法结果求和。
请你找出能够使上述结果小于等于阈值 threshold 的除数中 最小 的那个。
每个数除以除数后都向上取整,比方说 7/3 = 3 , 10/2 = 5 。
闭区间写法,注意max_element的使用!注意匿名函数的使用!
-
[]:不捕获任何变量lambda体内不能访问外部作用域的变量(除了全局变量和静态变量)。
-
[=]:以值捕获所有变量在lambda体内创建外部变量的副本。注意,在C++11中,这种方式捕获的变量默认是只读的(除非使用
mutable关键字)。 -
[&]:以引用捕获所有变量在lambda体内使用外部变量的引用,因此可以修改它们(如果变量不是常量)。
-
[var]:以值捕获特定变量var只捕获指定的变量
var(按值)。 -
[&var]:以引用捕获特定变量var只捕获指定的变量
var(按引用)。
最后,注意返回值,看注释!
class Solution {
public:int upper_div(int a,int b){if(a%b==0)return a/b;else return a/b+1;}int smallestDivisor(vector<int>& nums, int threshold) {int le=1;int ri = *max_element(nums.begin(), nums.end());//闭区间写法auto check=[&](int mid){int tot=0;for(int num:nums){tot+=upper_div(num,mid);if(tot>threshold)return false;}return true;};while(le<=ri){int mid=(ri-le)/2+le;if(check(mid)){ri=mid-1;}else le=mid+1;}return le;//记住,返回的是不满足对应的那个变量,即left(check代表满足)}
};再次强调灵神提出的循环不变量:
对于求最小的题目,开区间二分的写法,为什么最终返回的是 right,而不是别的数?在初始化(循环之前)、循环中、循环结束后,都时时刻刻保证 check(right) == true 和 check(left) == false,这就叫循环不变量。根据循环不变量,循环结束时 left + 1 == right,那么 right 就是最小的满足要求的数(因为再 −1 就不满足要求了),所以答案是 right。
2187.完成旅途的最少时间
给你一个数组 time ,其中 time[i] 表示第 i 辆公交车完成 一趟旅途 所需要花费的时间。
每辆公交车可以 连续 完成多趟旅途,也就是说,一辆公交车当前旅途完成后,可以 立马开始 下一趟旅途。每辆公交车 独立 运行,也就是说可以同时有多辆公交车在运行且互不影响。
给你一个整数 totalTrips ,表示所有公交车 总共 需要完成的旅途数目。请你返回完成 至少 totalTrips 趟旅途需要花费的 最少 时间。
开区间模版真好用!二分找答案!(非常好的思想和技巧,可作为解题时应该想到的点)
class Solution {
public:
typedef long long ll;long long minimumTime(vector<int>& time, int totalTrips) {int slow=*max_element(time.begin(),time.end());int len=time.size();ll le=0;ll ri=totalTrips/len;ri=ri*slow+3*len;if(len==0)return 0;else if(len==1)return (ll)totalTrips*time[0];auto check=[&](ll t){ll count=0;for(auto num:time){count+=t/num;}if(count>=totalTrips)return true;else return false;};while(le+1<ri){ll mid=(ri-le)/2+le;if(check(mid)){ri=mid;}else le=mid;}return le+1;}
};1011.在D天内送达包裹的能力
传送带上的包裹必须在 days 天内从一个港口运送到另一个港口。
传送带上的第 i 个包裹的重量为 weights[i]。每一天,我们都会按给出重量(weights)的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。
返回能在 days 天内将传送带上的所有包裹送达的船的最低运载能力。
其实二分查找套模板以外,还需要解决两个关键问题:第一个是初始边界le和ri的确定(注意是开区间);第二个是如何高效的设计check函数(灵神:往往涉及到贪心)
class Solution {
public:
typedef long long ll;int shipWithinDays(vector<int>& weights, int days) {int biggest=*max_element(weights.begin(),weights.end());int len=weights.size();ll tot=accumulate(weights.begin(),weights.end(),0LL);ll le=biggest-1;ll ri=tot;if(len==1)return weights[0];auto check=[&](ll temp){ll store=0;int z=0;for(int i=0;i<len;i++){if(store+weights[i]<=temp)store+=weights[i];else{store=weights[i];z++;}if(z>days)return false;}if(store!=0)z++;if(z>days)return false;return true;};while(le+1<ri){ll mid=(ri-le)/2+le;if(check(mid))ri=mid;else le=mid;}return (int)le+1;}
};475.供暖器
冬季已经来临。 你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。
在加热器的加热半径范围内的每个房屋都可以获得供暖。
现在,给出位于一条水平线上的房屋 houses 和供暖器 heaters 的位置,请你找出并返回可以覆盖所有房屋的最小加热半径。
注意:所有供暖器 heaters 都遵循你的半径标准,加热的半径也一样。
就是在模板基础上上面的两个关键问题!这里对于check函数,用双指针来优化(其目的也是利用之前的排序性质,前面已经举过的后面就不用再举了)
class Solution {
public:
typedef long long ll;int findRadius(vector<int>& houses, vector<int>& heaters) {sort(houses.begin(),houses.end());ll k=houses.size();sort(heaters.begin(),heaters.end());ll le=-1;ll ri=1e9;auto check=[&](ll mid){int i,j;for(i=0,j=0;i<houses.size()&&j<heaters.size(); ){if(houses[i]>=(ll)(heaters[j]-mid)&&houses[i]<=(ll)(heaters[j]+mid) )i++;else j++;}return i>=k;};while(le+1<ri){ll mid=(ri-le)/2+le;if(check(mid))ri=mid;else le=mid;}return (int)le+1;}
};2594.修车的最小时间
给你一个整数数组 ranks ,表示一些机械工的 能力值 。ranksi 是第 i 位机械工的能力值。能力值为 r 的机械工可以在 r * n2 分钟内修好 n 辆车。
同时给你一个整数 cars ,表示总共需要修理的汽车数目。
请你返回修理所有汽车 最少 需要多少时间。
注意:所有机械工可以同时修理汽车。
这里优化check函数的计算——用整数二分法计算每个机械工在给定时间内能修理的最大车辆数
同时,注意一下c++中经典的显示类型转换:
static_cast<ll>(rank) 将rank转为ll型
class Solution {
public:
typedef long long ll;long long repairCars(vector<int>& ranks, int cars) {ll le=-1;int len=ranks.size();int themin=*min_element(ranks.begin(),ranks.end());ll ri=(themin+1)*pow(cars,2);auto check = [&](ll time) {ll total_repaired = 0;for (int rank : ranks) {ll left = 0, right = cars;ll n_i = 0;while (left <= right) {ll mid = (left + right) / 2;if (mid * mid * static_cast<ll>(rank) <= time) {n_i = mid;left = mid + 1;} else {right = mid - 1;}}total_repaired += n_i;if (total_repaired >= cars) return true;}return false;};while(le+1<ri){ll mid=(ri-le)/2+le;if(check(mid))ri=mid;else le=mid;}return le+1;}
};1482.制作m束花所需的最小天数
给你一个整数数组 bloomDay,以及两个整数 m 和 k 。
现需要制作 m 束花。制作花束时,需要使用花园中 相邻的 k 朵花 。
花园中有 n 朵花,第 i 朵花会在 bloomDay[i] 时盛开,恰好 可以用于 一束 花中。
请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1
输入:bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3 输出:12 解释:要制作 2 束花,每束需要 3 朵。 花园在 7 天后和 12 天后的情况如下: 7 天后:[x, x, x, x, _, x, x] 可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花,因为它们不相邻。 12 天后:[x, x, x, x, x, x, x] 显然,我们可以用不同的方式制作两束花
同样是check函数,为了求在mid天时相邻的k个花有几簇,显然这种相邻的问题可以使用滑动窗口思想!
class Solution {
public:int minDays(vector<int>& bloomDay, int m, int k) {int le=-1;int ri=*max_element(bloomDay.begin(),bloomDay.end());int mid;int len=bloomDay.size();auto check=[&](int mid){int cons=0;int done=0;for(int i=0;i<len;i++){if(bloomDay[i]<=mid){cons++;if(cons==k){done++;cons=0;}}else if(bloomDay[i]>mid)cons=0;if(done>=m)return true;}return done>=m;};while(le+1<ri){mid=(ri-le)/2+le;if(check(mid))ri=mid;else le=mid;}if(check(ri))return le+1;else return -1;}
};上面是二分求最小,下面是二分求最大,其实也是一样的。不过有一些变化:
以开区间二分为例:
求最小:check(mid) == true 时更新 right = mid,反之更新 left = mid,最后返回 right。
求最大:check(mid) == true 时更新 left = mid,反之更新 right = mid,最后返回 left。
对于开区间写法,简单来说 check(mid) == true 时更新的是谁,最后就返回谁。
275.H指数2
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数,citations 已经按照 非降序排列 。计算并返回该研究者的 h 指数。
h 指数的定义:h 代表“高引用次数”(high citations),一名科研人员的 h 指数是指他(她)的 (n 篇论文中)至少 有 h 篇论文分别被引用了至少 h 次。
class Solution {
public:int hIndex(vector<int> &citations) {// 在区间 (left, right) 内询问int n = citations.size();int left = 0;int right = n + 1;while (left + 1 < right) { // 区间不为空// 循环不变量:// left 的回答一定为「是」// right 的回答一定为「否」int mid = (left + right) / 2;// 引用次数最多的 mid 篇论文,引用次数均 >= midif (citations[n - mid] >= mid) {left = mid; // 询问范围缩小到 (mid, right)} else {right = mid; // 询问范围缩小到 (left, mid)}}// 根据循环不变量,left 现在是最大的回答为「是」的数return left;}
};灵神的模板↑ 注意解释~
2226.每个小孩最多能分到多少糖果
给你一个 下标从 0 开始 的整数数组 candies 。数组中的每个元素表示大小为 candies[i] 的一堆糖果。你可以将每堆糖果分成任意数量的 子堆 ,但 无法 再将两堆合并到一起。
另给你一个整数 k 。你需要将这些糖果分配给 k 个小孩,使每个小孩分到 相同 数量的糖果。每个小孩可以拿走 至多一堆 糖果,有些糖果可能会不被分配。
返回每个小孩可以拿走的 最大糖果数目 。
#include <vector>
#include <algorithm>
using namespace std;class Solution {
public:int maximumCandies(vector<int>& candies, long long k) {long long max_val = *max_element(candies.begin(), candies.end());long long le = 0; long long ri = max_val + 1; auto check = [&](long long candy) -> bool {if (candy == 0) return true; long long cnt = 0; for (int c : candies) {cnt += static_cast<long long>(c) / candy; if (cnt >= k) return true; }return cnt >= k; };while (le + 1 < ri) {long long mid = le + (ri - le) / 2; if (check(mid)) {le = mid; // 可行,尝试增大candy} else {ri = mid; // 不可行,减小candy}}return static_cast<int>(le); }
};2982.找出出现至少三次的最长特殊子字符串
给你一个仅由小写英文字母组成的字符串 s 。
如果一个字符串仅由单一字符组成,那么它被称为 特殊 字符串。例如,字符串 "abc" 不是特殊字符串,而字符串 "ddd"、"zz" 和 "f" 是特殊字符串。
返回在 s 中出现 至少三次 的 最长特殊子字符串 的长度,如果不存在出现至少三次的特殊子字符串,则返回 -1 。
子字符串 是字符串中的一个连续 非空 字符序列。
找到了一个小tips!!!管他最后返回le还是ri,我用一个变量ans记录最值?
class Solution {
public:int maximumLength(string s) {int len=s.size();int le=-1;int ri=len;unordered_map<char,vector<pair<int,int>>>store;for(int i=0;i<len;i++){char base=s[i];int count=0;int sta=i;while(i<len&&base==s[i]){count++;i++;}i--;store[base].push_back(make_pair(sta,count));}auto check=[&](int len){for(auto it=store.begin();it!=store.end();it++){char base=it->first;vector<pair<int,int>>temp=it->second;int count=0;int k=temp.size();for(int j=0;j<k;j++){if(temp[j].second<len)continue;else count+=(temp[j].second-len+1);if(count>=3)return true;}}return false;};int ans=0;while(le+1<ri){int mid=(ri-le)/2+le;if(check(mid)){le=mid;ans=max(ans,mid);}else ri=mid;}return ans==0?-1:ans;}
};二分查找之查找间接值
3143.正方形中的最多点数
给你一个二维数组 points 和一个字符串 s ,其中 points[i] 表示第 i 个点的坐标,s[i] 表示第 i 个点的 标签 。
如果一个正方形的中心在 (0, 0) ,所有边都平行于坐标轴,且正方形内 不 存在标签相同的两个点,那么我们称这个正方形是 合法 的。
请你返回 合法 正方形中可以包含的 最多 点数。
注意:
- 如果一个点位于正方形的边上或者在边以内,则认为该点位于正方形内。
- 正方形的边长可以为零
这里就是典型的二分查找间接值——正方形的边长,但注意求的事正方形中包含的最多点数——这种往往涉及到一些统计量的额外引入。
注意排序,经典错误是对 points 做了 sort 但没有同步调整 s,导致标签和点不再对应
struct P {int x, y;char c;P(int x,int y,char c):x(x),y(y),c(c){}
};
class Solution {
public:// 返回按 |x| 排序后,最后一个满足 |x| <= len 的下标(若没有返回 -1)int findin(const vector<P>& pts, int len) {int l = -1, r = (int)pts.size();while (l + 1 < r) {int m = l + (r - l) / 2;if (abs(pts[m].x) <= len) l = m;else r = m;}return l;}int check(const vector<P>& pts, int len) {int pos = findin(pts, len);if (pos == -1) return 0; // 没有任何点满足 |x|<=lenunordered_set<char> seen;for (int i = 0; i <= pos; ++i) {if (abs(pts[i].y) <= len) {if (seen.find(pts[i].c) != seen.end()) return -1; seen.insert(pts[i].c);}}return (int)seen.size();}int maxPointsInsideSquare(vector<vector<int>>& points, string s) {int n = points.size();if (n == 0) return 0;// 合并点和标签,避免排序后标签失配vector<P> pts;pts.reserve(n);int maxAbs = 0;for (int i = 0; i < n; ++i) {P p{points[i][0], points[i][1], s[i]};pts.push_back(p);maxAbs = max(maxAbs, max(abs(p.x), abs(p.y)));}sort(pts.begin(), pts.end(), [](const P& a, const P& b) {if (abs(a.x) != abs(b.x)) return abs(a.x) < abs(b.x);return abs(a.y) < abs(b.y);});int lo = -1, hi = maxAbs + 1;int ans = 0;while (lo + 1 < hi) {int mid = lo + (hi - lo) / 2;int k = check(pts, mid);if (k != -1) {lo = mid;ans = max(ans, k);} else {hi = mid;}}return ans;}
};
二分查找之最小化最大值
2064.分配给商店的最多商品的最小值
给你一个整数 n ,表示有 n 间零售商店。总共有 m 种产品,每种产品的数目用一个下标从 0 开始的整数数组 quantities 表示,其中 quantities[i] 表示第 i 种商品的数目。
你需要将 所有商品 分配到零售商店,并遵守这些规则:
- 一间商店 至多 只能有 一种商品 ,但一间商店拥有的商品数目可以为 任意 件。
- 分配后,每间商店都会被分配一定数目的商品(可能为
0件)。用x表示所有商店中分配商品数目的最大值,你希望x越小越好。也就是说,你想 最小化 分配给任意商店商品数目的 最大值 。
请你返回最小的可能的 x 。
对于最小化最大值,灵神的原话是:好比用一个盖子(上界)去压住最大值,看看能否压住(check 函数)
所以可以看到这里和前面是类似反过来的(即check满足时缩小的是ri);此外,关于最后的返回值,不是一定哪个为false返回哪个,更多的还是要从意义入手:ri所代表的mid是满足条件的最后一个值,所以返回它(你也可以返回le+1)
class Solution {
public:int minimizedMaximum(int n, vector<int>& quantities) {int m=quantities.size();int le=-1;int ri=*max_element(quantities.begin(),quantities.end())+1;auto check=[&](int mid){int count=0;if(mid==0)return false;for(int i=0;i<m;i++){if(quantities[i]%mid==0)count+=(quantities[i]/mid);else count+=quantities[i]/mid+1;if(count>n)return false;}return count<=n;};while(le+1<ri){int mid=(ri-le)/2+le;if(check(mid))ri=mid;else le=mid;}return ri;}
};二分查找之最大化最小值
3281.范围内整数的最大得分
给你一个整数数组 start 和一个整数 d,代表 n 个区间 [start[i], start[i] + d]。
你需要选择 n 个整数,其中第 i 个整数必须属于第 i 个区间。所选整数的 得分 定义为所选整数两两之间的 最小 绝对差。
返回所选整数的 最大可能得分 。
输入: start = [6,0,3], d = 2
输出: 4
解释:
可以选择整数 8, 0 和 4 获得最大可能得分,得分为 min(|8 - 0|, |8 - 4|, |0 - 4|),等于 4。
二分答案结合贪心思想,总结很精辟:

再次强调,看到最大化最小值和最小化最大值这种要思考二分!
代码的规整性,对初始不知道怎么写的时候可以采取下一次思想(把下一次的提前面)
class Solution {
public:typedef long long ll;int maxPossibleScore(vector<int>& start, int d) {sort(start.begin(),start.end());int len=start.size();ll le=-1;ll ri=start[len-1]-start[0]+d+2;ll ans=0;auto check=[&](ll score){ll bench=INT_MIN;//下一次的起点for(int i=0;i<len;i++){bench=max(bench+score,(ll)start[i]);if(bench>start[i]+d)return false;}return true;};while(le+1<ri){ll mid=(ri-le)/2+le;if(check(mid)){ans=max(ans,mid);le=mid;}else ri=mid;}return ans;}
};找第k小/第k大
378.有序矩阵中第k小的元素
给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
你必须找到一个内存复杂度优于 O(n2) 的解决方案。
首先这种肯定也是可以二分的,最小值是矩阵左上角,最大值是矩阵右下角
然后从右上角(二叉搜索树)开始搜索 贴一个灵神的:
class Solution {
public:int kthSmallest(vector<vector<int>>& matrix, int k) {int n = matrix.size();auto check = [&](int mx) -> bool {int cnt = 0; // matrix 中的 <= mx 的元素个数int i = 0, j = n - 1; // 从右上角开始while (i < n && j >= 0 && cnt < k) {if (matrix[i][j] > mx) {j--; // 排除第 j 列} else {cnt += j + 1; // 从 matrix[i][0] 到 matrix[i][j] 都 <= mxi++;}}return cnt >= k;};int left = matrix[0][0] - 1;int right = matrix[n - 1][n - 1];while (left + 1 < right) {int mid = left + (right - left) / 2;(check(mid) ? right : left) = mid;}return right;}
};