最短路spfa和多层图（P1073 [NOIP 2009 提高组] 最优贸易）题解

题目3

P1073 [NOIP 2009 提高组] 最优贸易 - 洛谷

目的时在一个地方以最低买入价格买入商品，再寻找另一个节点，以最高的售价卖出

但是这道题没有边权，只有点权。还有值得注意的一点是有些边不是双向边。

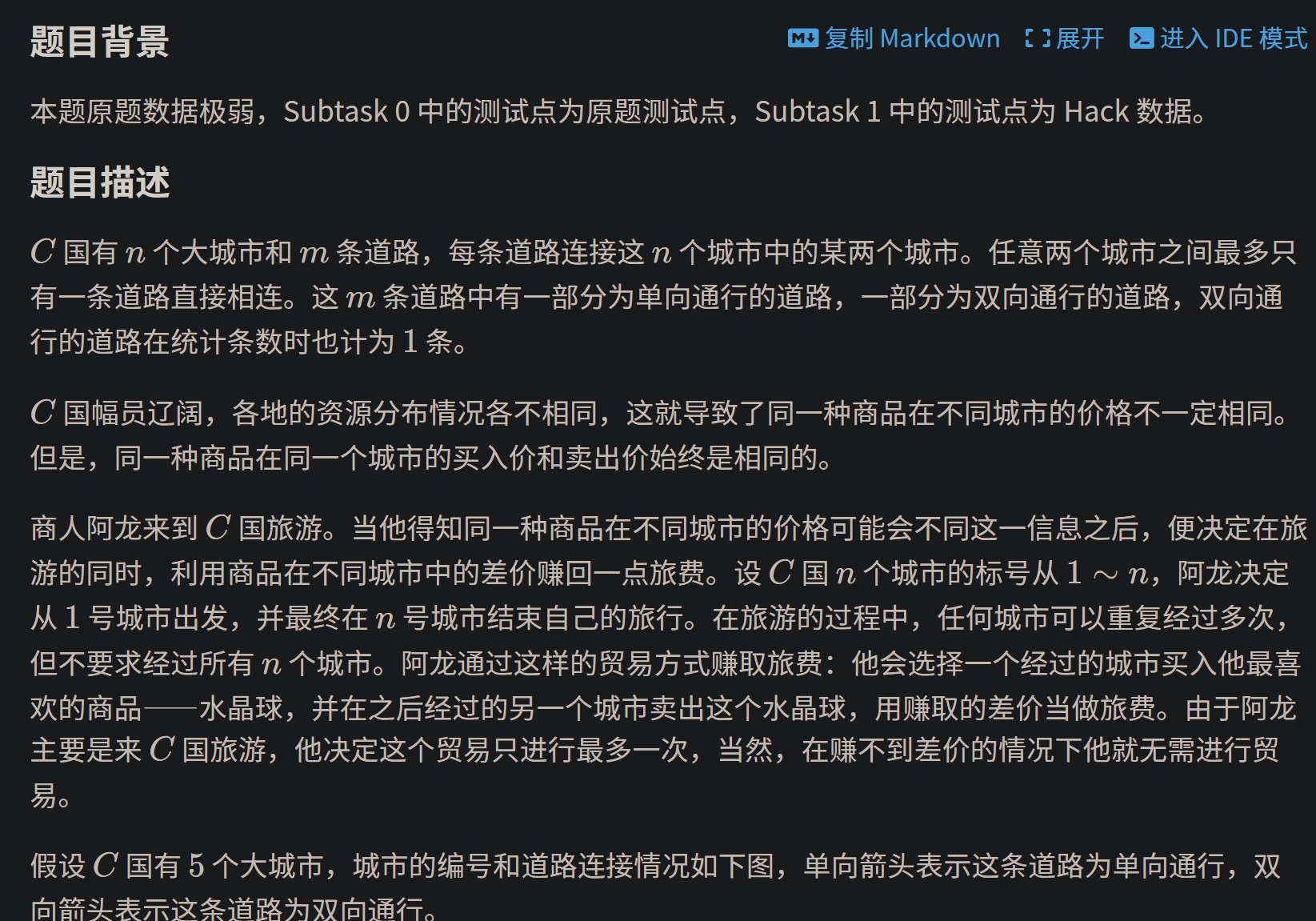
当我们输入每个点的点权时，不妨重新建一层图：

1→2层表示买入值，2→3表示卖出，从1-n点的权值最大

由于可以任意走动，所以我们可以建一张图，令图上的边全都是0，表示走动对我最终的结果没有影响。

买入操作：建立一条有向边转移到一张新图上，边的大小为-v[i]，指向点i所能到达的点（在第二层图上）。

卖出操作：建立一条有向边转移到第三层图上，边的大小为v[i]，指向i所能到达的点（在第三层图上）。

可以发现，从第一层图走到第二层图走到第三层图走到终点，这就是一个合法的选择。

来看建图的代码：

for(int i=1;i<=n;i++){int c=read();add(i,i+n,-c),add(i+n,i+2*n,c);
}
for(int i=1;i<=m;i++){int x,y,z;x=read();y=read();z=read();if(z==1){add(x,y);add(x+n,y+n);add(x+2*n,y+2*n);}else{add(x,y);add(x+n,y+n);add(x+2*n,y+2*n);add(y,x);add(y+n,x+n);add(y+2*n,x+2*n);}
}

读入点权的时候，连当前点到下一层图的同样编号的点一条边，边权为当前点的点权。

因为第一层到第二层代表的是在当前节点买入，所以这样的边权表示他"赚了"a元，当然他现在买入东西是亏钱了，所以可以看作赚了-a元。同样，第二层到第三层表示卖出去了东西，那么两点之间的边权表示他赚了b元。如此一来，讲这俩的权加上就表示他一共赚了多少。

为什么不能用dijkstra呢？

因为明显按照上述思路会有负权，也会有环。所以我们选择spfa

来看spfa部分

void spfa(){memset(d,-0x7f,sizeof(d));queue<int>q;q.push(1);book[1]=true;d[1]=0;while(!q.empty()){int x=q.front();q.pop();book[x]=false;for(int i=head[x];i;i=ne[i]){int y=to[i];if(d[y]<d[x]+v[i]){d[y]=d[x]+v[i];if(!book[y]){book[y]=true;q.push(y);}}}}
}

先对于处理权的数组附上极大值，然后将起点(1)加入队列，把1到1的权设置为0；然后在队列非空的前提下找更大的值。也就是找最长路。因为上面也讲了，我们需要计算从起点到终点的赚钱最多。支出的钱已经是负数，所以我们只需要求边权相加最大即可

值得注意的是，如果d[3*n]，因为第三层表示卖出，所以d[3*n]表示最终结果。如果它是负数，就表示赚不到钱，输出0；

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=3e6+5;
int read(){int s=0,fl=1;char w=getchar();while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}return fl*s;
}
void out(int x){if(x<0)putchar('-'),x=-x;if(x<10)putchar(x+'0');else out(x/10),putchar(x%10+'0');
}
int n,m;
int v[N],head[N],ne[N],to[N],tot,d[N];
bool book[N];
void add(int x,int y,int t=0){to[++tot]=y;ne[tot]=head[x];head[x]=tot;v[tot]=t;
}
void spfa(){memset(d,-0x7f,sizeof(d));queue<int>q;q.push(1);book[1]=true;d[1]=0;while(!q.empty()){int x=q.front();q.pop();book[x]=false;for(int i=head[x];i;i=ne[i]){int y=to[i];if(d[y]<d[x]+v[i]){d[y]=d[x]+v[i];if(!book[y]){book[y]=true;q.push(y);}}}}
}
int main(){n=read();m=read();for(int i=1;i<=n;i++){int c=read();add(i,i+n,-c),add(i+n,i+2*n,c);}for(int i=1;i<=m;i++){int x,y,z;x=read();y=read();z=read();if(z==1){add(x,y);add(x+n,y+n);add(x+2*n,y+2*n);}else{add(x,y);add(x+n,y+n);add(x+2*n,y+2*n);add(y,x);add(y+n,x+n);add(y+2*n,x+2*n);}}spfa();out(d[3*n]<0?0:d[3*n]);return 0;
}