图论Day5学习心得
prim算法
53. 寻宝(第七期模拟笔试)
最小生成树是所有节点的最小连通子图,即:以最小的成本(边的权值)将图中所有节点链接到一起。
图中有n个节点,那么一定可以用n-1条边将所有节点连接到一起。
那么如何选择这n-1条边就是最小生成树算法的任务所在。
那么在这个图中,如何选取n-1条边使得图中所有节点连接到一起,并且边的权值和最小呢?
(图中为n为7,即7个节点,那么只需要n-1即6条边就可以讲所有顶点连接到一起)
prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。
prim算法核心就是三步,
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
在prim算法中,有一个数组特别重要,minDist。
每次寻找距离最小生成树最近的节点并加入到最小生成树中”,那么如何寻找距离最小生成树最近的节点呢?
这就用到了minDist数组,它用来作什么呢?
minDist数组用来记录每一个节点距离最小生成树的最近距离。理解这一点非常重要,这也是prim算法最核心要点所在
#1 初始状态
minDist数组里的数值初始化为最大数,因为本题节点距离不会超过10000,所以初始化最大数为10001就可以。
现在还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面在比较的时候,发现更近的距离,才能更新到minDist数组上。
如图:
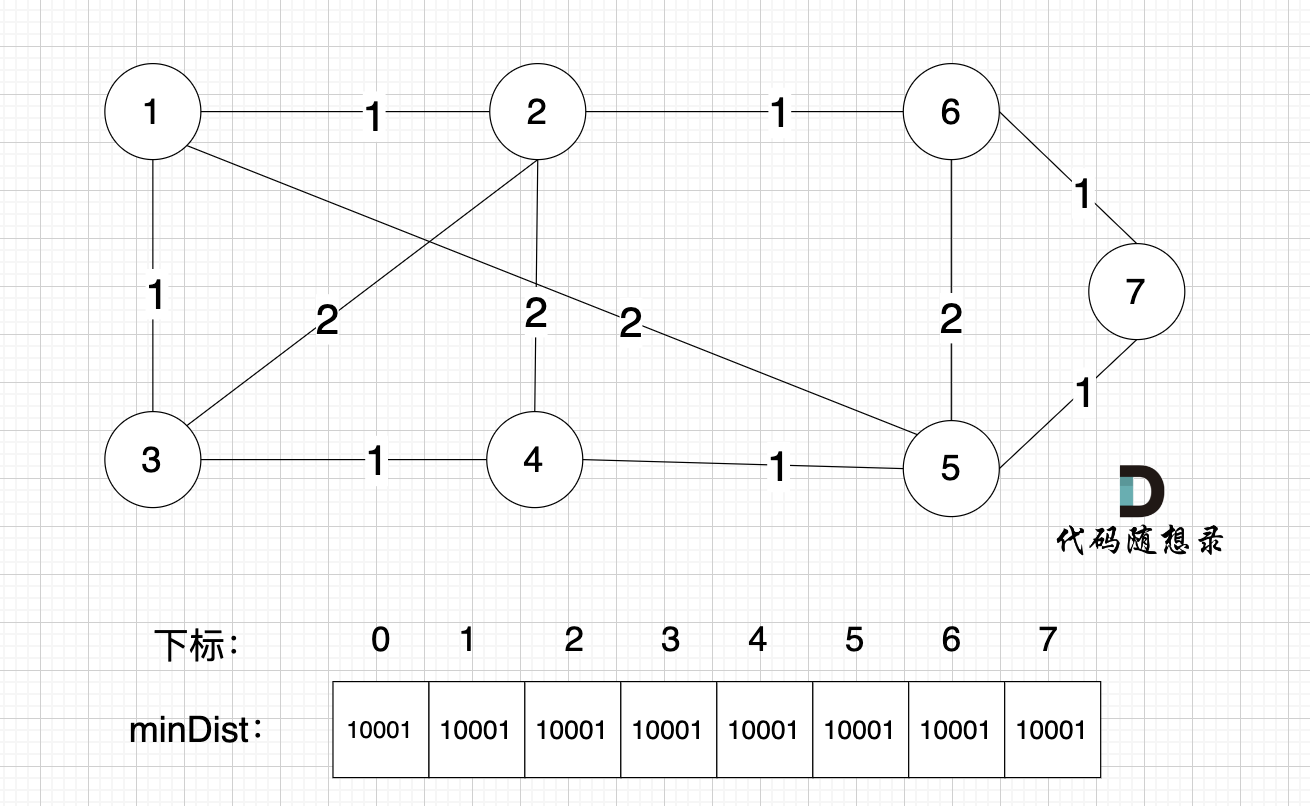
开始构造最小生成树
#2
1、prim三部曲,第一步:选距离生成树最近节点
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那选择节点1(符合遍历数组的习惯,第一个遍历的也是节点1)
2、prim三部曲,第二步:最近节点加入生成树
此时节点1已经算最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来,要更新所有节点距离最小生成树的距离,如图:
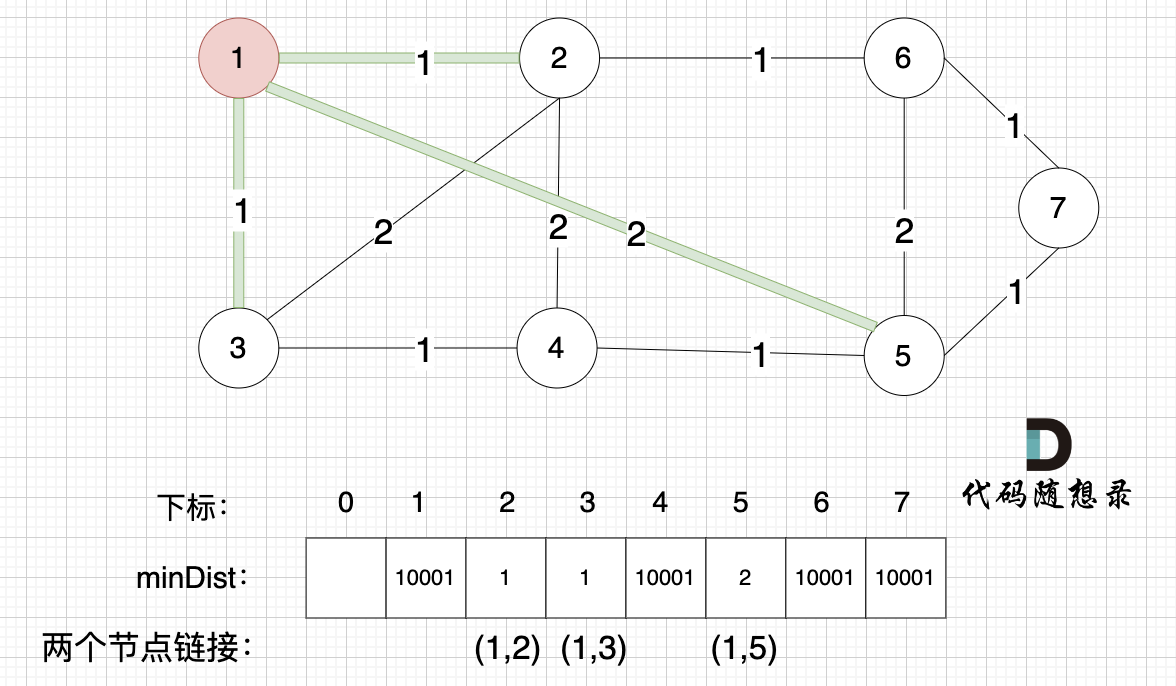
注意下标0,就不管它了,下标1与节点1对应,这样可以避免大家把节点搞混。
此时所有非生成树的节点距离最小生成树(节点1)的距离都已经跟新了。
- 节点2与节点1的距离为1,比原先的距离值10001小,所以更新minDist[2]。
- 节点3和节点1的距离为1,比原先的距离值10001小,所以更新minDist[3]。
- 节点5和节点1的距离为2,比原先的距离值10001小,所以更新minDist[5]。
注意图中标记了minDist数组里更新的权值,是哪两个节点之间的权值,例如minDist[2]=1,这个1是节点1与节点2之间的连线,清楚这一点对最后我们记录最小生成树的权值总和很重要。
#3
1、prim三部曲,第一步:选距离生成树最近节点
选取一个距离最小生成树(节点1)最近的非生成树里的节点,节点2,3,5距离最小生成树(节点1)最近,选节点2(其实选节点3或者节点2都可以,距离一样的)加入最小生成树。
2、prim三部曲,第二步:最近节点加入生成树
此时节点1和节点2,已经算最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来,要更新节点距离最小生成树的距离,如图:
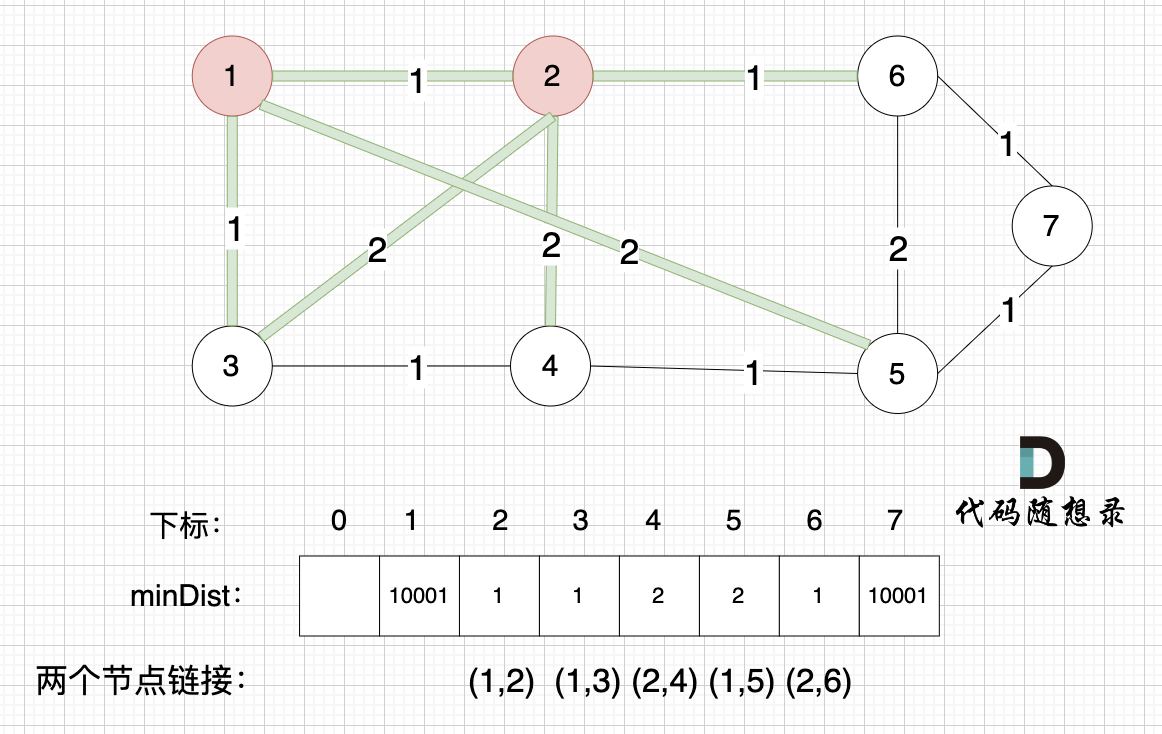
此时所有非生成树的节点距离最小生成树(节点1、节点2)的距离都已经跟新了。
- 节点3和节点2的距离为2,和原先的距离值1小,所以不用更新。
- 节点4和节点2的距离为2,比原先的距离值10001小,所以更新minDist[4]。
- 节点5和节点2的距离为10001(不连接),所以不用更新。
- 节点6和节点2的距离为1,比原先的距离值10001小,所以更新minDist[6]。
#4
1、prim三部曲,第一步:选距离生成树最近节点
选择一个距离最小生成树(节点1、节点2)最近的非生成树里的节点,节点3,6距离最小生成树(节点1、节点2)最近,选节点3(选节点6也可以,距离一样)加入最小生成树。
2、prim三部曲,第二步:最近节点加入生成树
此时节点1、节点2、节点3算是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:
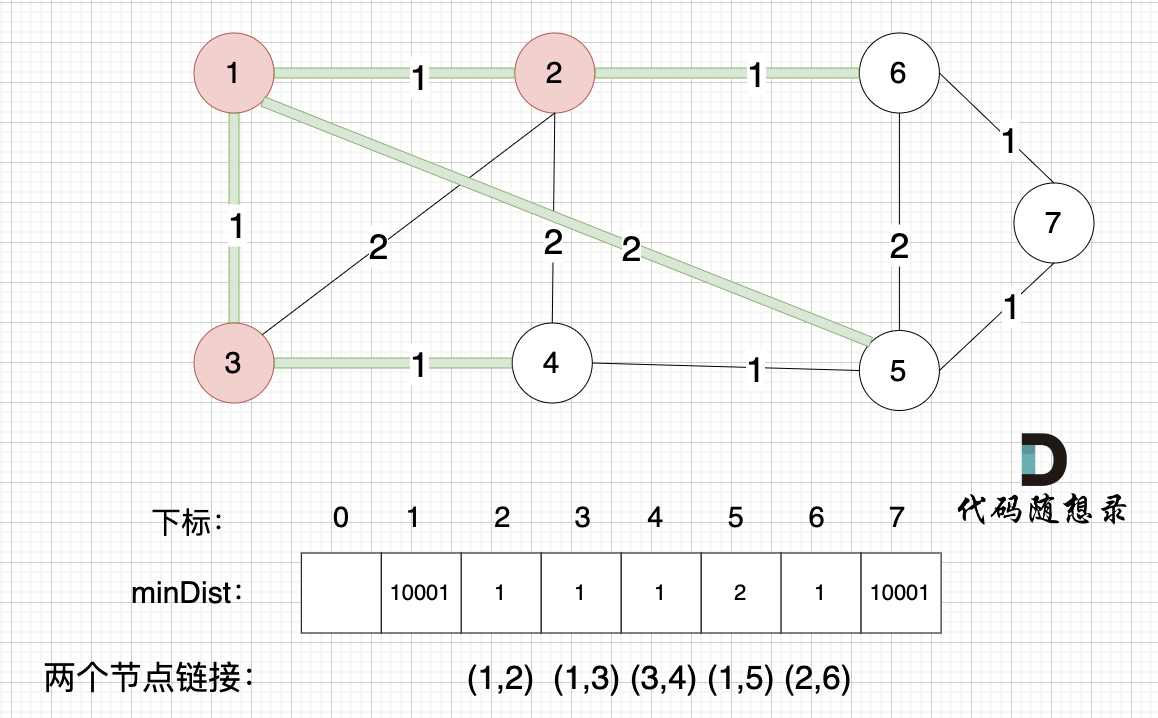
所有非生成树的节点距离最小生成树(节点1、节点2、节点3)的距离都已经跟新了。
- 节点4和节点3的距离为1,和原先的距离值2小,所以更新minDist[4]为1。
上面为什么只比较节点4和节点3的距离呢?
因为节点3加入最小生成树后,非生成树节点只有节点4和节点3是链接的,所以需要重新更新一下节点4距离最小生成树的距离,其他节点距离最小生成树的距离都不变。
#5
1、prim三部曲,第一步:选距离生成树最近节点
继续选择一个距离最小生成树(节点1、节点2、节点3)最近的非生成树里的节点,
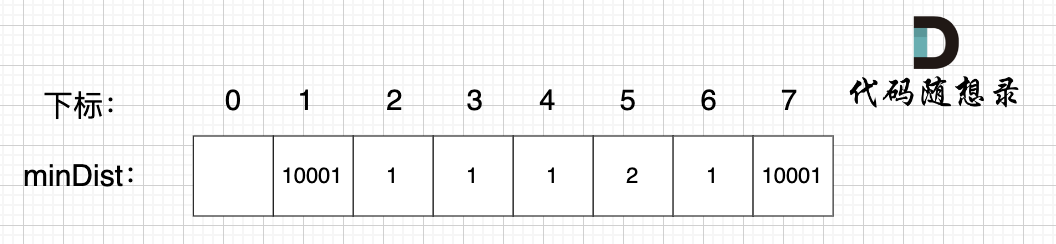
minDist数组是记录了所有非生成树节点距离生成树的最小距离,所以从数组里能看出来,非生成树节点4和节点6距离生成树最近。
任选一个加入生成树,我们选节点4(选节点6也行)。
注意,根据minDist数组,选取距离生成树最近的节点加入生成树,那么minDist数组里记录的其实也是最小生成树的边的权值(我在图中把权值对应的是哪两个节点也标记出来了)。
2、prim三部曲,第二步:最近节点加入生成树
此时节点1、节点2、节点3、节点4算是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:
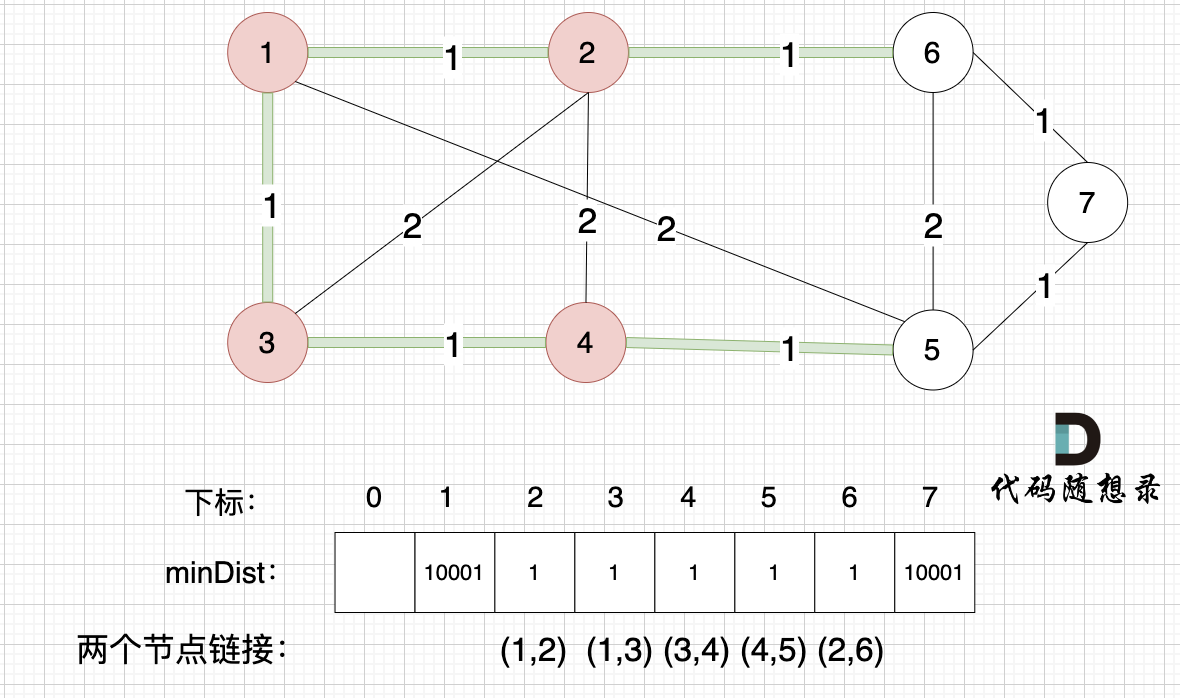
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4)的距离。
- 节点5和节点4的距离为1,和原先的距离值2小,所以更新minDist[5]为1。
#6
1、prim三部曲,第一步:选距离生成树最近节点
继续选距离最小生成树(节点1、节点2、节点3、节点4)最近的非生成树里的节点,只有节点5和节点6。
选节点5(选节点6也可以)加入生成树。
2、prim三部曲,第二步:最近节点加入生成树
节点1、节点2、节点3、节点4、节点5算是最小生成树的节点。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
接下来更新节点距离最小生成树的距离,如图:
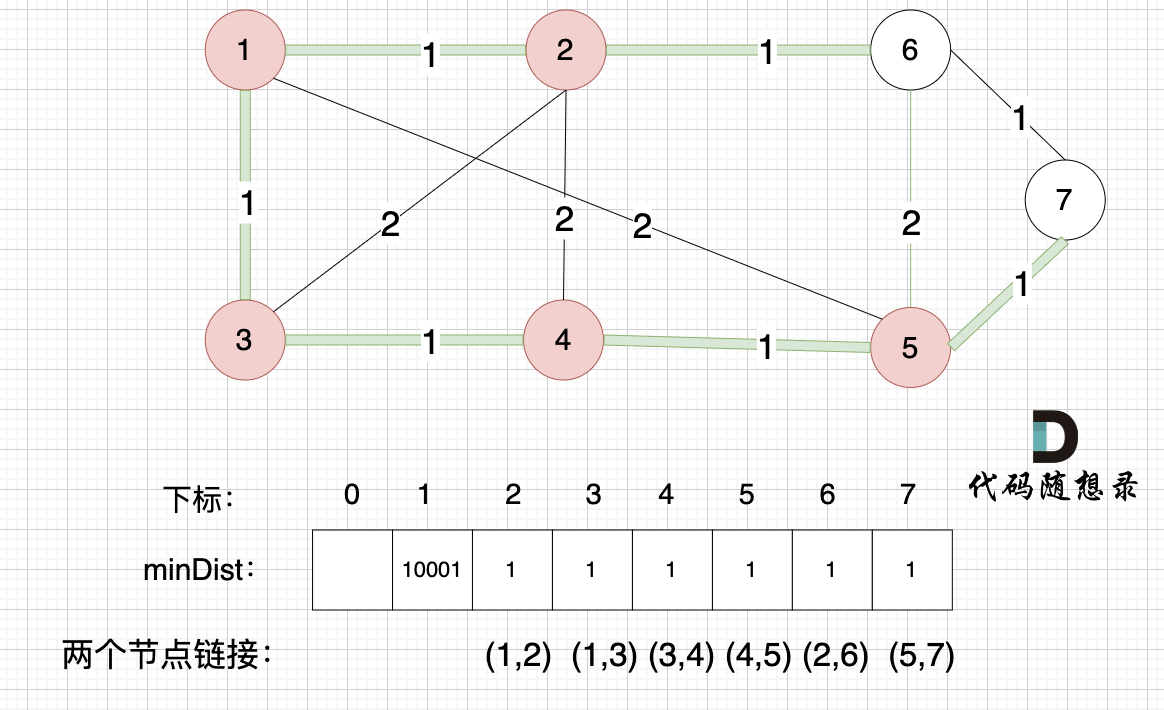
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4、节点5)的距离。
- 节点6和节点5距离为2,比原先的距离值1大,所以不更新
- 节点7和节点5距离为1,比原先的距离值10001小,更新minDist[7]
#7
1、prim三部曲,第一步:选距离生成树最近节点
继续选距离最小生成树(节点1、节点2、节点3、节点4、节点5)最近的非生成树里的节点,只有节点6和节点7。
2、prim三部曲,第二步:最近节点加入生成树
选节点6(选节点7也行,距离一样的)加入生成树。
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
节点1、节点2、节点3、节点4、节点5、节点6算是最小生成树的节点,接下来更新节点距离最小生成树的距离,如图:
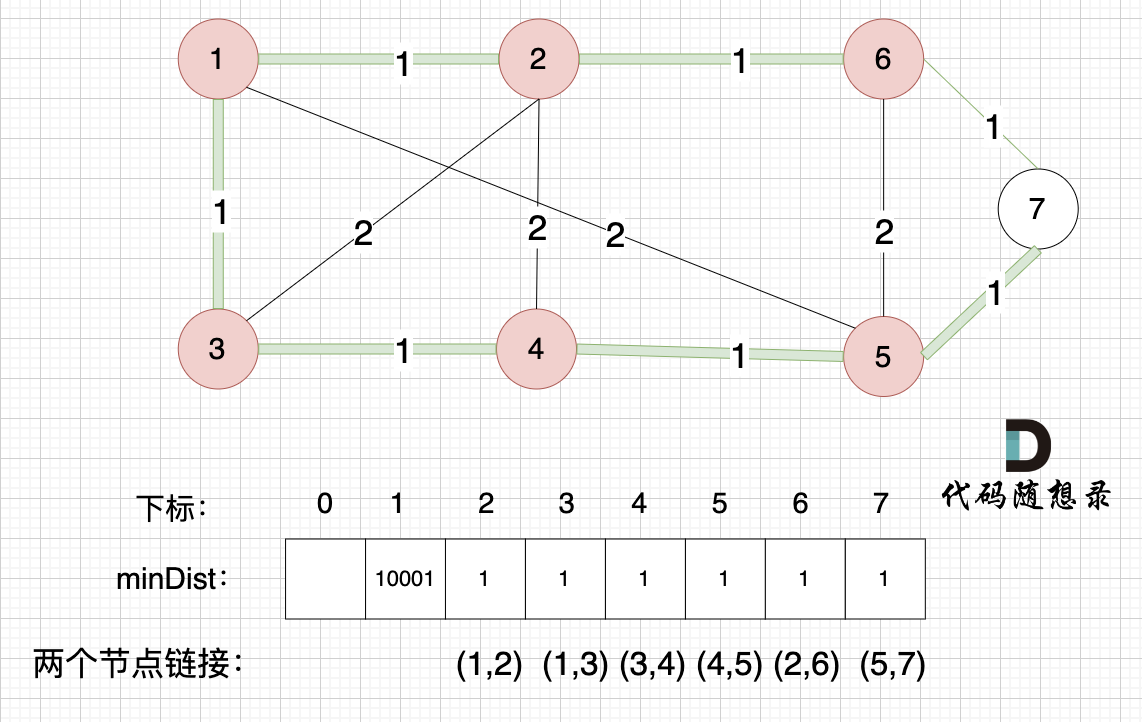
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
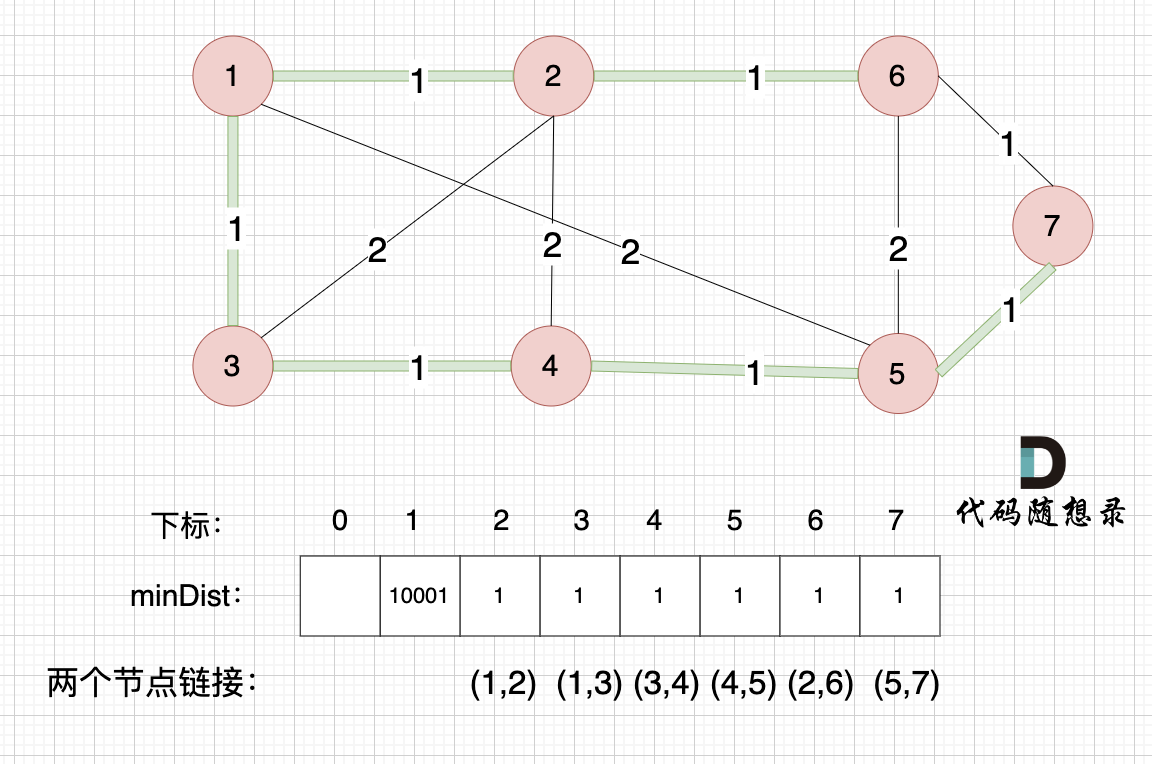
#最后
最后就生成了一个最小生成树,绿色的边将所有节点链接到一起,并且保证权值是最小的,因为我们在更新minDist数组的时候,都是选距离最小生成树最近的点加入到树中。
最后,minDist数组也就是记录的是最小生成树所有边的权值。
#include<iostream>
#include<vector>
#include <climits>using namespace std;
int main() {int v, e;int x, y, k;cin >> v >> e;// 填一个默认最大值,题目描述val最大为10000vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));while (e--) {cin >> x >> y >> k;// 因为是双向图,所以两个方向都要填上grid[x][y] = k;grid[y][x] = k;}// 所有节点到最小生成树的最小距离vector<int> minDist(v + 1, 10001);// 这个节点是否在树里vector<bool> isInTree(v + 1, false);// 我们只需要循环 n-1次,建立 n - 1条边,就可以把n个节点的图连在一起for (int i = 1; i < v; i++) {// 1、prim三部曲,第一步:选距离生成树最近节点int cur = -1; // 选中哪个节点 加入最小生成树int minVal = INT_MAX;for (int j = 1; j <= v; j++) { // 1 - v,顶点编号,这里下标从1开始// 选取最小生成树节点的条件:// (1)不在最小生成树里// (2)距离最小生成树最近的节点if (!isInTree[j] && minDist[j] < minVal) {minVal = minDist[j];cur = j;}}// 2、prim三部曲,第二步:最近节点(cur)加入生成树isInTree[cur] = true;// 3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)// cur节点加入之后, 最小生成树加入了新的节点,那么所有节点到 最小生成树的距离(即minDist数组)需要更新一下// 由于cur节点是新加入到最小生成树,那么只需要关心与 cur 相连的 非生成树节点 的距离 是否比 原来 非生成树节点到生成树节点的距离更小了呢for (int j = 1; j <= v; j++) {// 更新的条件:// (1)节点是 非生成树里的节点// (2)与cur相连的某节点的权值 比 该某节点距离最小生成树的距离小// 很多录友看到自己 就想不明白什么意思,其实就是 cur 是新加入 最小生成树的节点,那么 所有非生成树的节点距离生成树节点的最近距离 由于 cur的新加入,需要更新一下数据了if (!isInTree[j] && grid[cur][j] < minDist[j]) {minDist[j] = grid[cur][j];}}}// 统计结果int result = 0;for (int i = 2; i <= v; i++) { // 不计第一个顶点,因为统计的是边的权值,v个节点有 v-1条边result += minDist[i];}cout << result << endl;}
