密码学系列 - 零知识证明(ZKP) - 多种承诺方案
在 ZKP 中使用的承诺方案的示例
- 基于哈希的承诺:证明者生成他们希望承诺的值的加密哈希,并将该哈希发送给验证者。然后,证明者可以稍后显示该值,验证者可以验证显示的值是否与哈希匹配。
- Pedersen 承诺:证明者通过将随机值与生成器相乘并添加他们希望承诺的值来生成承诺。证明者可以稍后通过显示随机值和生成器来显示该值,验证者可以验证显示的值是否与承诺匹配。
- 多项式承诺:在多项式承诺中,证明者通过提供对多项式系数的承诺来对多项式做出承诺。验证者稍后可以通过检查多项式在特定点的计算结果是否为特定值来验证承诺。
- 在 ZKP 中使用多项式承诺,可以通过向验证者隐藏多项式系数的值来提供隐私性,并通过确保只有知道系数值的人才能做出承诺来提供可验证性。多项式承诺是各种零知识证明系统(包括 zk-SNARK 和 zk-STARK)的重要组成部分,使它们能够实现简洁性。
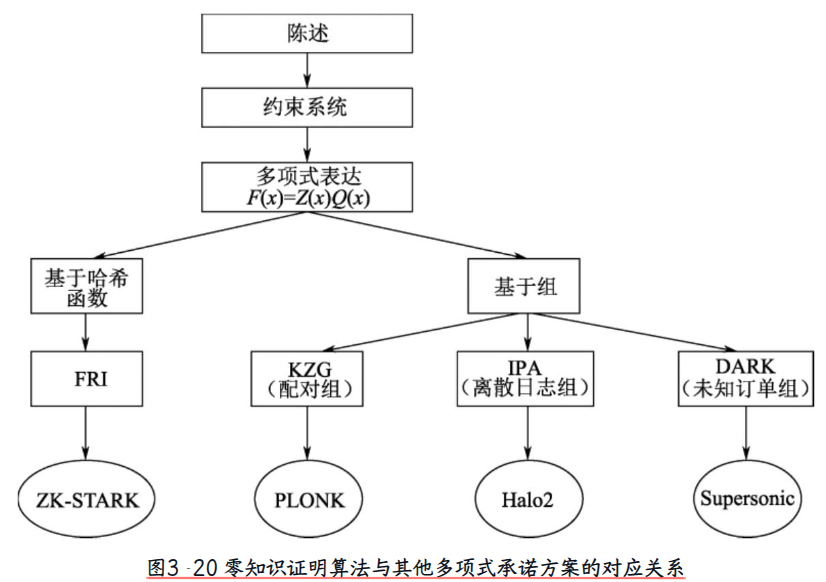
多种 多项式承诺 方案
最常用的方法有FRI承诺、KZG10承诺、IPA承诺、DARKS承诺(基于格)等,其中,
- FRI承诺是基于哈希函数实现的
- KZG10承诺是基于配对组实现的
- IPA承诺是基于离散日志组实现的
- DARKS承诺是基于未知订单组实现的。
构造 SNARKs 的4种类型
有四种类型的假设被用来构造 SNARKs,或者更普遍地说,有四种类型的假设被用来构造初始化式承诺方案。
- 基于配对的,我们有(多项式承诺)
KZG及其变体(KZG10)。(Halo 和 Halo 2 采用椭圆曲线配对和多项式承诺) - 基于离散对数的,我们有基于
IPA的Bulletproofs及其变体。 - 基于哈希的方案,我们有
FRI和许多其它的方案。使用Arc折叠 - 基于格 (格哈希非常快,比普通哈希快),
DARKS
FRI承诺
FRI即Fast Reed-Solomon IOPP,FRI承诺的核心是对要承诺的多项式进行“折叠”,通过“折叠”将一个计算次数很高的多项式逐步转化为计算次数较低、验证者可以接受的计算复杂度的多项式。
- Reed-Solomon (一种纠删码, 基于离散傅里叶变换的系统 , 复制因子是 1/2)
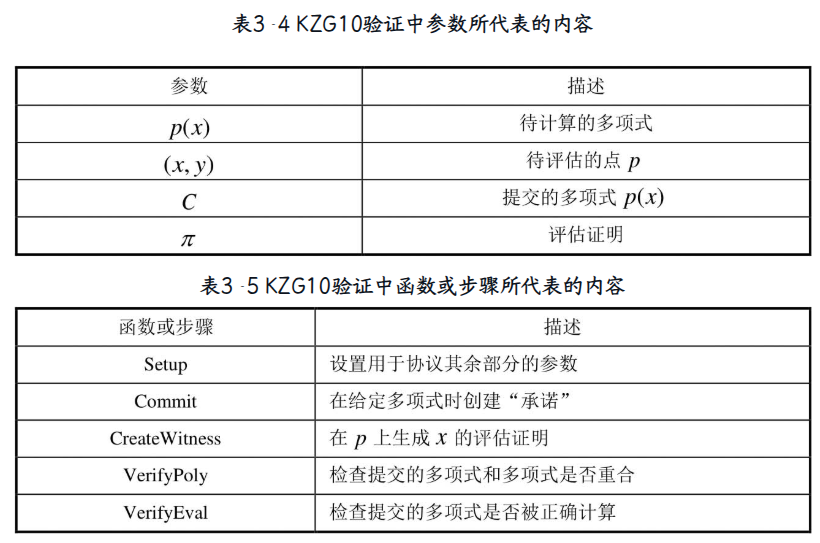
KZG10承诺
KZG承诺[插图]基于配对组,其主要优点是承诺和打开仅由恒定数量的群元素组成,缺点是它需要一个结构化参数字符串,其长度与承诺的多项式系数的数量一样长
与FRI承诺相比,KZG10承诺有一些独特的功能,它不是对某个字节做出的承诺,而是对多项式的承诺。此外,由于KZG承诺是基于配对的,其证明规模恒定,为单个椭圆曲线组元素数量,验证时间恒定,所以仅需进行两次配对操作
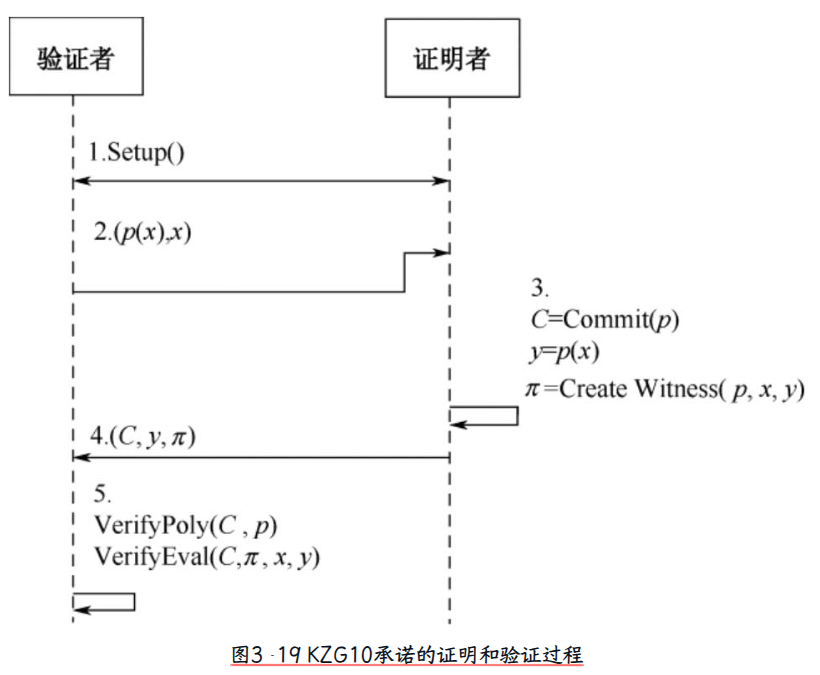
IPA承诺
零知识证明BulletProofs、Halo2算法的核心是IPA承诺,也称内积证明。IPA承诺的安全假设较少,不需要配对,也不需要可信设置。
不同 多项式承诺方案 的对比
3.4.4 不同方案的对比不同的零知识证明算法的关键差别,是它们采用了不同的多项式承诺方案。
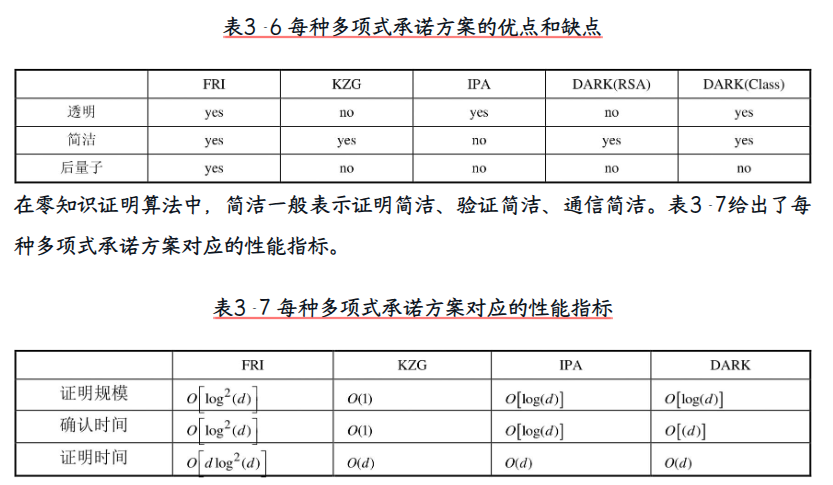
KZG承诺方案在简洁方面是最好的,因为它的证明规模和验证时间都是恒定的,这意味着电路规模的增加不会导致证明规模的增加。其他多项式承诺方案的证明规模与电路规模有关,这意味着证明规模会随着电路规模的增大而增大。但是在安全性方面,KZG承诺方案与其他方案相比较差,因为它需要第三方可信设置。
- 往期精彩回顾:
- 区块链知识系列
- 密码学系列
- 零知识证明系列
- 共识系列
- 公链调研系列
- BTC系列
- 以太坊系列
- EOS系列
- Filecoin系列
- 联盟链系列
- Fabric系列
- 智能合约系列
- Token系列
