二叉搜索树的模拟实现

一，引言

为了实现更加快速的搜索数据，以及不局限于数组形式的存储数据，引入二叉搜索树这一数据结构。二叉搜索树有以下特点：

1，首先二叉搜索树是一颗二叉树。

2，若它的左⼦树不为空，则左⼦树上所有结点的值都⼩于等于根结点的值。

3，若它的右⼦树不为空，则右⼦树上所有结点的值都⼤于等于根结点的值。

4，它的左右⼦树也分别为⼆叉搜索树。

举个例子如下：

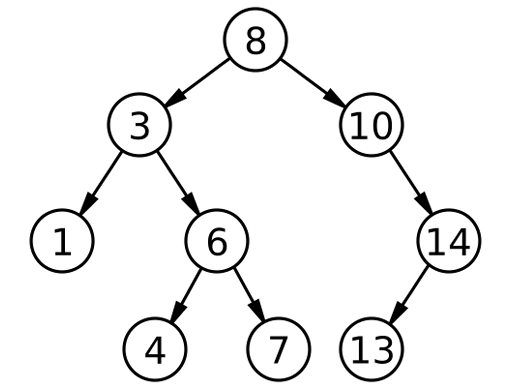
如上图：每一棵左子树的值都小于等于根节点。每一棵右子树的值都大于等于根节点。每一棵子树也满足上述规则。

二，时间复杂度分析

最优情况下，⼆叉搜索树为完全⼆叉树(或者接近完全⼆叉树)，其⾼度为 log2^N 。

最差情况下，⼆叉搜索树退化为单⽀树(或者类似单⽀)，其⾼度为：N。

所以综合⽽⾔⼆叉搜索树增删查改时间复杂度为:O(N)。

虽然在O(N)的时间复杂度在查找算法上并不占优势，但是二叉搜索树的插入规则为以后的AVLTree以及红黑树做准备。

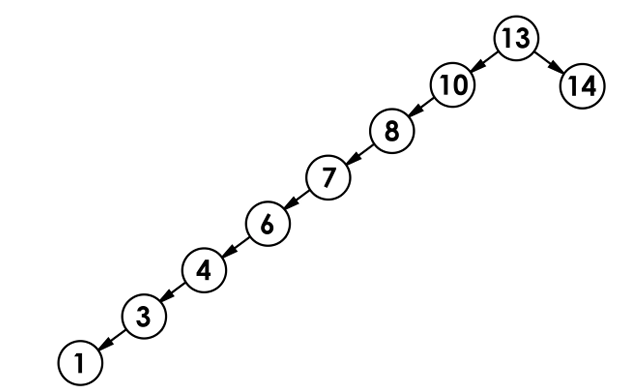
如上图：在这种特殊的二叉搜索树的时间复杂度就近似于O(N) 。

三，二叉搜索树的插入

在上述了解了二叉搜索树的实现规则之后，在实现二叉搜索树的插入之前要先讲解一下，每一个二叉搜索树的单个节点。

在二叉搜索树中每一个节点由四部分组成：关键字(key)变量--负责在二叉搜索树中进行比较，并且不能进行修改；值(value)每一个关键字(key)对应一个value ，value是可以进行修改，并且不参与比较逻辑，指向左孩子的指针，指向右孩子的指针。四个部分如下：

template<class K, class V>struct BSTNode{K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;BSTNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}};

BSTNode对该对象实现初始化操作，走初始化列表。

实现单个节点的创建之后。开始实现二叉搜索树的插入，首先创建二叉搜索树的大框架模型如下：

template<class K, class V>class BSTree{//typedef BSTNode<K> Node;using Node = BSTNode<K, V>;public:// 强制生成构造BSTree() = default;
private:Node* _root = nullptr;};
}

开始插入节点，若是首次插入节点，则直接将根节点(_root)指向该新节点；若不是新插入的节点，则从根节点开始比较，插入的key大于根节点的key，指向该根节点的指针向右到右孩子的位置，若插入的key小于根节点的key，指向该节点的指针向左到左孩子的位置，若两者的key相等则直接返回false。代码如下：

bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}

这里parent指针指向cur的父类节点，当cur为nullptr，该节点指向new出来新的节点。此时需要cur的父类节点(parent)。在cur指向new的节点之前，需要先进行标记父类节点，以防止找不到父类节点。

四，二叉搜索树的查找

查找规则和插入规则相似，从根节点(_root)开始一步步进行判断，若大于key的值，则根节点向右到右孩子节点。一步步进行判断，若key相等，则返回true。如果到nullptr节点依然没有找到相对应的key，则返回false 。代码如下：

bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}

五，删除关键字为(key)的节点

删除节点和插入节点不同。删除节点非为一下三种情况：
1，要删除的左右节点同时都为空如图：

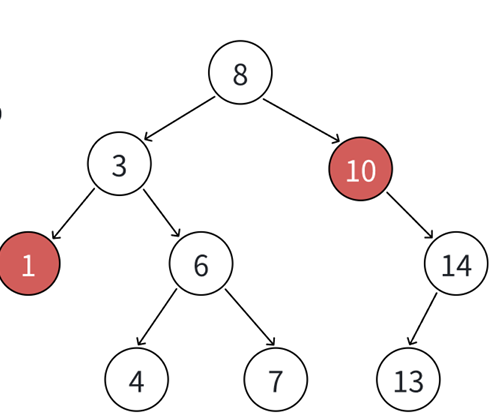
如图当删除1这个节点，只需要将该节点delete之后，父类位置对应的向下节点置空。

2，要删除的左右节点有一个为空，如上图的10，把删除结点的⽗亲对应孩⼦指针指向删除节点的左孩子或右孩⼦，直接删除需要删除的结点。如图：

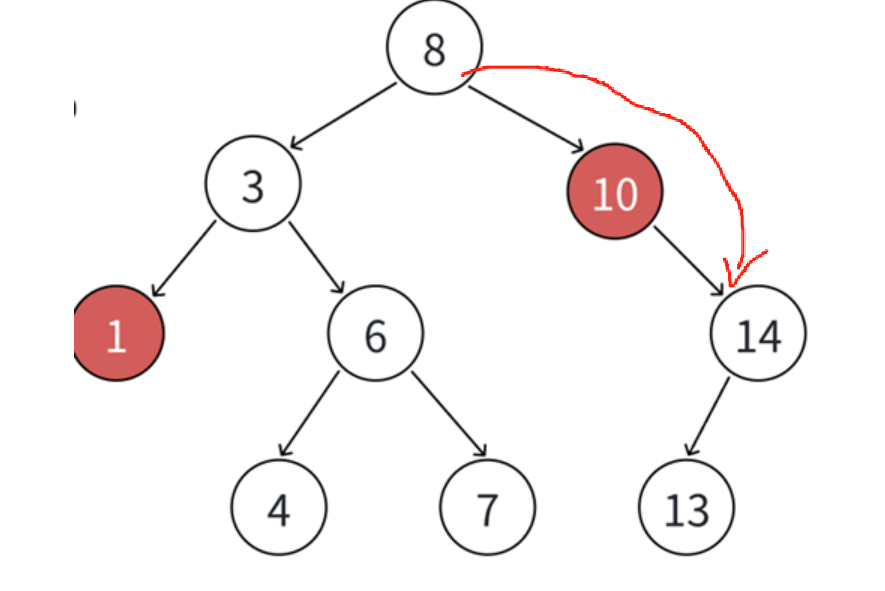
3，删除节点的两个孩子都有节点。如图：

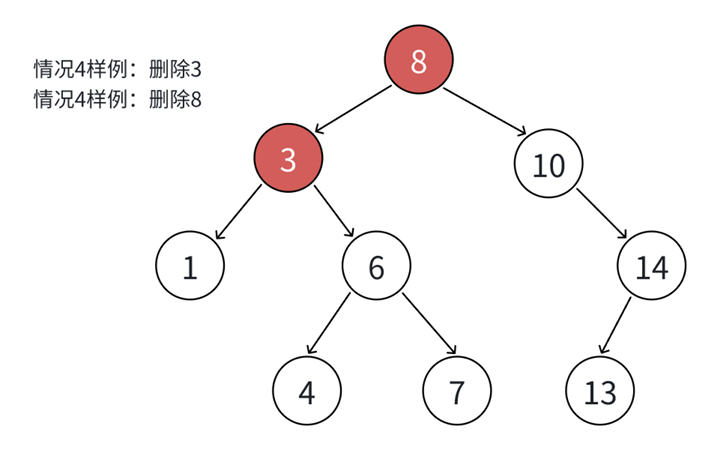
这时无法直接删除对应位置的节点，需要用到替换法进行删除：找N左⼦树的值最⼤结点 R(最右结点)或者N右⼦树的值最⼩结点R(最左结点)替代N，因为这两个结点中任意⼀个，放到N的 位置，都满⾜⼆叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换，转⽽变成删除R结 点，R结点符合情况1或情况2，可以直接删除。如上图可以将3替换成（左子树的最大节点1  ；右子树的最小节点4）；将8替换成（左子树的最大节点7   ；右子树的最小节点10）。

代码实现如下：

bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{// 右为空if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{// 左右都不为空// 右子树最左节点Node* replaceParent = cur;Node* replace = cur->_right;while (replace->_left){replaceParent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replaceParent->_left == replace)replaceParent->_left = replace->_right;elsereplaceParent->_right = replace->_right;delete replace;}return true;}}return false;}

第一步找到删除的位置，第二步判断该删除节点的位置输入上述哪种情况，前两种情况需要又分为删除的节点是否为根节点，这两种需要单独进行编写。第三种情况如上代码样例，需要先找右子树的最左节点。找到之后进行key的替换，最后删除右子树的最左节点。这里的删除需要注意：需要一个该节点的父类节点进行标记，逻辑和插入节点类似。

六，总结

二叉搜索树总体的逻辑不难理解，比较复杂的是删除操作。需要注意的是由于单个节点并没有设置指向父类的指针，因此尤其注意在删除和插入对父类节点的标记。